Macierze

Wprowadzenie do macierzy

Drukuj

Poziom studiów

Macierz - to uporządkowana tabela liczb ułożona w wierszach i kolumnach.

Oto przykładowe macierze: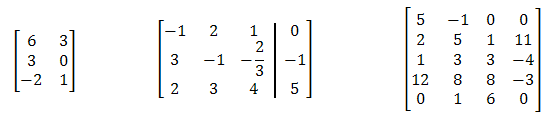

W poniższym filmie podaję podstawowe informacje na temat macierzy (pierwsze 20 minut filmu).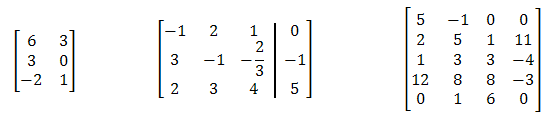

W tym nagraniu opowiadam o przedmiotach, które najczęściej pojawiają się na początku studiów: o algebrze liniowej (macierze) i geometrii analitycznej.

Czas nagrania: 33 min.

Macierze ułatwiają rozwiązywanie układów równań liniowych. Każdy układ równań liniowych można zapisać za pomocą macierzy.

Układowi równań: \[ \left\{\begin{array}{c} -x+2 y+z=0 \\ 3 x-y-\frac{2}{3} z=-1 \\ 2 x+3 y+4 z=5 \end{array}\right. \] odpowiada macierz: \[ \left[\begin{array}{ccc|c} -1 & 2 & 1 & 0 \\ 3 & -1 & -\frac{2}{3} & -1 \\ 2 & 3 & 4 & 5 \end{array}\right] \]

Liczby w macierzy, to współczynniki liczbowe z układu równań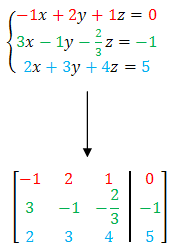

Pionowa kreska, w powyższej macierzy, oddziela współczynniki wolne, stojące po prawej stronie znaków równości. Nie ma konieczności pisania tej kreski. Stosuje się ją tylko w celu uzyskania lepszej przejrzystości.

W każdej macierzy możemy wyróżnić kolumny oraz wiersze.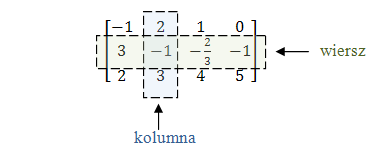

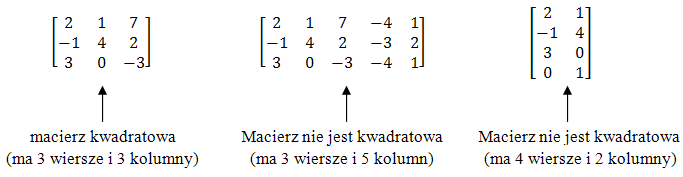
Jeżeli macierz ma tyle samo wierszy co kolumn, to mówimy że jest macierzą kwadratową.

Na macierzach można wykonywać różne działania. Zazwyczaj wykonuje się je w celu doprowadzenia macierzy do postaci schodkowej uporządkowanej, z której można odczytać rozwiązania układu równań.
Wszystkie działania zostaną dokładnie omówione w następnych rozdziałach.