Operacje elementarne na macierzach
Poziom studiów
Na macierzach (podobnie jak na układach równań) można wykonywać trzy proste operacje: - dodać do jednego wiersza macierzy inny wiersz pomnożony przez liczbę,
- zamienić dwa wiersze miejscami,
- mnożyć wiersz przez liczbę różną od zera.
Te trzy opisane powyżej operacje nazywamy operacjami elementarnymi na wierszach.
Operacje elementarne na wierszach macierzy odpowiadają takim samym operacjom na równaniach układu równań.
Rozważ układ równań: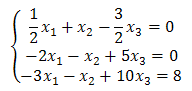 
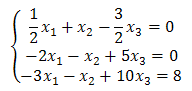
Danemu układowi równań odpowiada następująca macierz: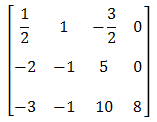 
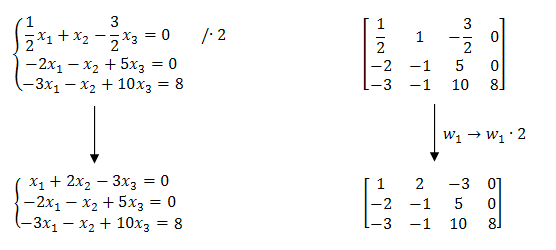
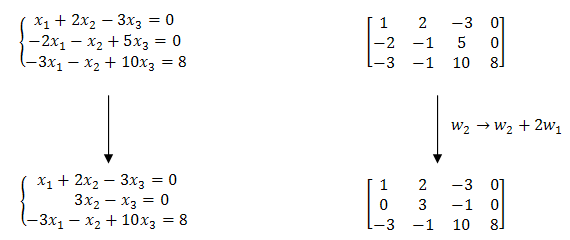W wyniku powyższej operacji pozbyliśmy się jednej niewiadomej z drugiego równania.
Teraz pozbędziemy się niewiadomej \(x_1\) z trzeciego równania. W tym celu do trzeciego równania dodajemy pierwsze równanie pomnożone przez \(3\):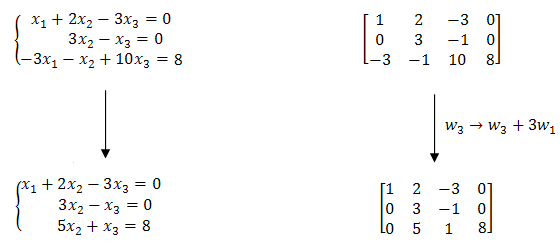
Teraz będziemy pozbywać się kolejnych niewiadomych maksymalnie upraszczając układ równań (oraz macierz). Wykonywane operacje elementarne będą zapisywane przy strzałkach.
Wykonanie wszystkich powyższych operacji elementarnych doprowadziło nas do rozwiązania układu równań: 
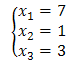Ciągłe przepisywanie całego układu równań jest dość czasochłonne. Dlatego warto wykonywać działania jedynie na macierzy odpowiadającej danemu układowi, aby na końcu tylko odczytać z niej rozwiązanie.
Przy takim podejściu całe zadanie sprowadza się do przekształcenia macierzy na postać schodkową zredukowaną. Z takiej postaci od razu widać rozwiązania układu równań.
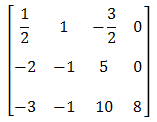
Wykonamy teraz kilka operacji elementarnych na równaniach układu i jednocześnie na wierszach odpowiadającej mu macierzy.
Na początku pomnóżmy pierwszy wiersz przez liczbę \(2\): 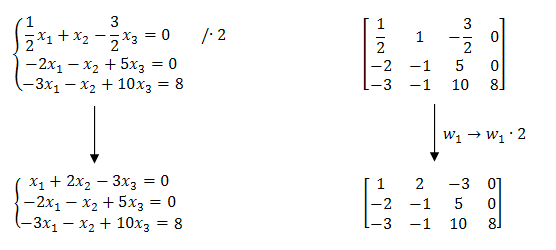Napis \(w_1 \rightarrow w_1\cdot 2\) jest symbolicznym zapisem tego, że "wiersz pierwszy przekształcamy w wiersz pierwszy pomnożony przez \(2\)".
Teraz do drugiego wiersza dodajemy pierwszy wiersz pomnożony przez \(2\): 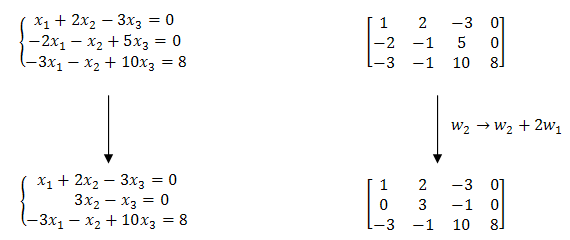W wyniku powyższej operacji pozbyliśmy się jednej niewiadomej z drugiego równania.Teraz pozbędziemy się niewiadomej \(x_1\) z trzeciego równania. W tym celu do trzeciego równania dodajemy pierwsze równanie pomnożone przez \(3\):
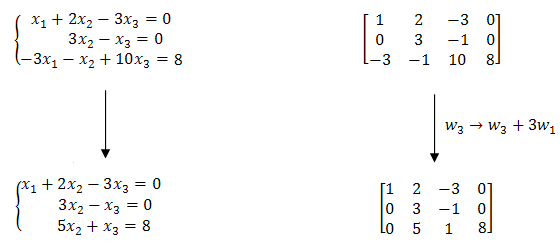Teraz będziemy pozbywać się kolejnych niewiadomych maksymalnie upraszczając układ równań (oraz macierz). Wykonywane operacje elementarne będą zapisywane przy strzałkach. Wykonanie wszystkich powyższych operacji elementarnych doprowadziło nas do rozwiązania układu równań: 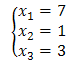Ciągłe przepisywanie całego układu równań jest dość czasochłonne. Dlatego warto wykonywać działania jedynie na macierzy odpowiadającej danemu układowi, aby na końcu tylko odczytać z niej rozwiązanie.Przy takim podejściu całe zadanie sprowadza się do przekształcenia macierzy na postać schodkową zredukowaną. Z takiej postaci od razu widać rozwiązania układu równań.
Tematy nadrzędne i sąsiednie