Sprowadzanie macierzy do postaci schodkowej zredukowanej
Poziom studiów
Mówimy, że macierz \(A\in M_{m\times n}(\mathbb{R} )\) jest w postaci schodkowej, jeżeli \(A\) spełnia warunki:
- każdy wiersz zerowy (składający się z samych zer) znajduje się poniżej każdego wiersza niezerowego,
- w każdym wierszu pierwszy (licząc od lewej) niezerowy wyraz znajduje się w kolumnie stojącej na prawo od pierwszego niezerowego wyrazu wiersza poprzedniego.
Mówiąc intuicyjnie - macierz jest w postaci schodkowej, jeżeli w kolejnych wierszach występuje na początku coraz więcej zer (kolejne wiersze macierzy przypominają schodki).
W tym nagraniu pokazuje na kilku przykładach jak wygląda macierz w postaci schodkowej zredukowanej.
Czas lekcji: 8 min.
Przykładowy macierzy zapisanych w postaci schodkowej: 

Przykłady macierzy które nie są zapisane w postaci schodkowej: 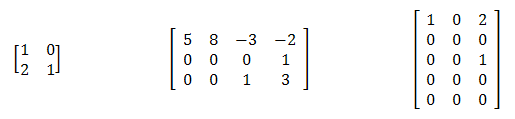
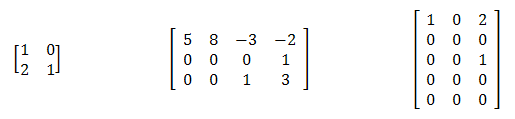
Definicja
Mówimy, że macierz jest w zredukowanej postaci schodkowej, jeżeli spełnia warunki:- jest w postaci schodkowej,
- w każdym wierszu pierwszy niezerowy wyraz jest równy \(1\), a ponadto inne wyrazy w jego kolumnie są zerami.
Przykładowy macierzy zapisanych w zredukowanej postaci schodkowej: 

Fakt
Każdą macierz można za pomocą operacji elementarnych sprowadzić do postaci schodkowej zredukowanej. Powyższy fakt jest niezwykle ważny, ponieważ dzięki niemu możemy rozwiązywać dowolnie skomplikowane układy równań liniowych. Wystarczy sprowadzić do postaci schodkowej zredukowanej macierz odpowiadającą takiemu układowi, a następnie odczytać z niej rozwiązanie.
Już w poprzednim rozdziale, podczas wykonywania operacji elementarnych, sprowadziliśmy macierz do postaci schodkowej zredukowanej. Wszystkie rachunki są przedstawione w tym przykładzie.
Poniżej podam kolejne przykłady na sprowadzanie macierzy do postaci schodkowej zredukowanej. Operacje elementarne na wierszach będziemy oznaczali tak jak we wspomnianym przykładzie.
Sprowadź podaną macierz do postaci schodkowej zredukowanej. 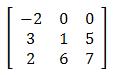
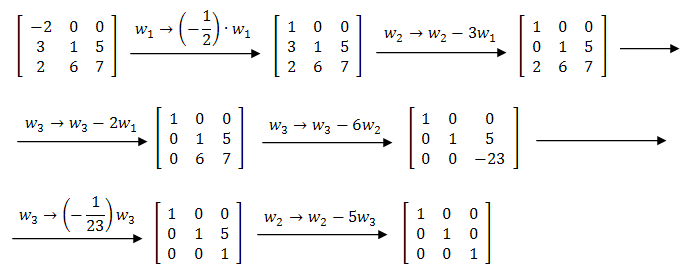
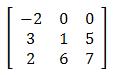
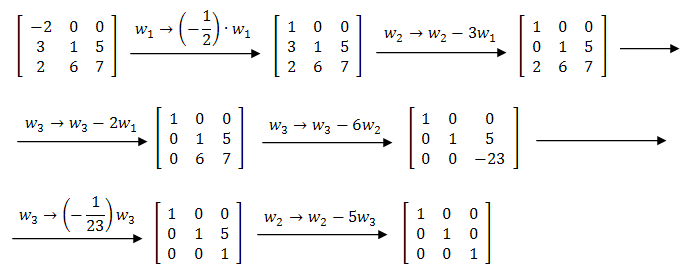
Sprowadź podaną macierz do postaci schodkowej zredukowanej.
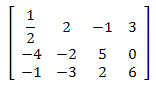
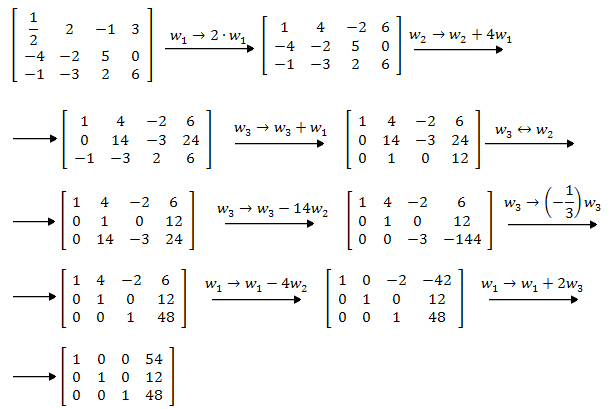
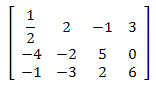
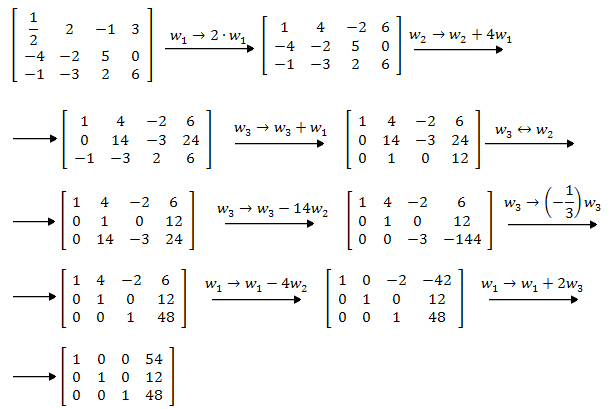
Tematy nadrzędne i sąsiednie