Liczby zespolone

Wprowadzenie do liczb zespolonych

Drukuj

Poziom studiów

Zbiór liczb zespolonych oznaczamy symbolem \(\mathbb{C} \) (ang. complex number).

W zbiorze liczb zespolonych można wyciągać pierwiastki z liczb ujemnych (co nie jest dozwolone w zbiorze liczb rzeczywistych \(\mathbb{R} \)).

Pierwiastek (parzystego stopnia) z liczby ujemnej jest tzw. liczbą urojoną i zapisujemy go za pomocą jednostki urojonej \(i\).

Definicja

Jednostka urojona \(i\) podniesiona do kwadratu daje \(-1\), czyli: \[i^2=-1\]

Jeżeli \(x\in \mathbb{R}\), to równanie \(x^2=-1\) nie ma rozwiązań.
Jeżeli \(x\in \mathbb{C}\), to równanie \(x^2=-1\) ma dwa rozwiązania: \[ x^2=-1\\[6pt] x=i\quad \lor \quad x=-i \]

W zbiorze liczb zespolonych rozwiąż równanie \(x^2=-9\)

\[ x^2=-9\\[6pt] x=3i\quad \lor \quad x=-3i \] ponieważ: \[(3i)^2=9\cdot i^2=9\cdot (-1)=-9\] oraz \[(-3i)^2=9\cdot i^2=9\cdot (-1)=-9\]

Definicja

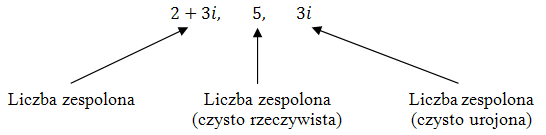
Liczbę zespoloną można zapisać tak: \[a+bi\] gdzie: \(a,b\in \mathbb{R} \).
Nazewnictwo:

\(a\) - część rzeczywista
\(b\) - część urojona
\(i\) - jednostka urojona

Liczba zespolona może składać się tylko z części rzeczywistej lub tylko z części urojonej. W szczególności każda liczba rzeczywista jest liczbą zespoloną.

W tym nagraniu wideo omawiam najważniejsze wiadomości dotyczące liczb zespolonych.
Na filmiku są omówione:

definicja liczby zespolonej,
interpretacja geometryczna i algebraiczna,
sprzężenie, moduł i argument liczby zespolonej,
zasady wykonywania działań na liczbach zespolonych,
wzór de Moivre'a.

Czas filmu: 53 minuty.