Jesteś tutaj: Szkoła → Elementy analizy matematycznej
Elementy analizy matematycznej
1.
WprowadzenieWprowadzenie
Analiza matematyczna zajmuje się analizowaniem funkcji.
Metody analizy pozwalają badać funkcje bardziej skomplikowane niż funkcja liniowa czy kwadratowa.
Jeżeli musimy zbadać funkcję wielomianową albo wymierną, to metody analizy matematycznej nadają się do tego doskonale.
Metody analizy pozwalają badać funkcje bardziej skomplikowane niż funkcja liniowa czy kwadratowa.
Jeżeli musimy zbadać funkcję wielomianową albo wymierną, to metody analizy matematycznej nadają się do tego doskonale.
Na czym polega analizowanie funkcji?
Na przykład na:- znalezieniu argument \(x\) dla którego funkcja przyjmuje wartość największą,
- wyznaczeniu zbioru wartości funkcji,
- zbadaniu monotoniczności funkcji,
- wyznaczeniu dziedziny, miejsc zerowych
- znalezieniu ekstremów lokalnych funkcji,
- zbadaniu granic funkcji.
Weźmy przykładową funkcję wymierną: \[\require{color}\color{maroon}{f(x)=\frac{6x^3+4x^2+12}{(x-3)(1-3x^2-x)}}\] Metody analizy matematycznej umożliwiają nam wyznaczenie własności charakterystycznych takiej funkcji, a w konsekwencji narysowanie wykresu: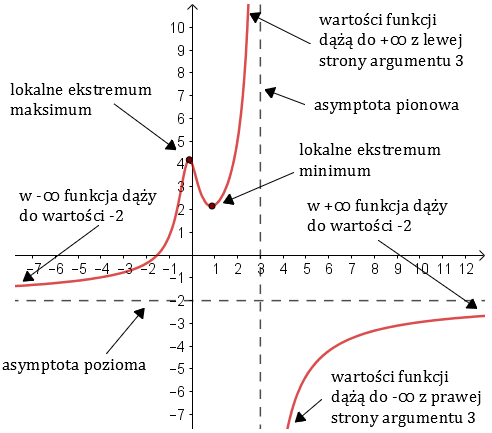 
Wszystkie elementy podpisane na powyższym wykresie można wyznaczyć metodami analizy. Mając wyznaczone te elementy możemy narysować wykres i odczytać z niego zbiór wartości funkcji.
Wszystkie elementy podpisane na powyższym wykresie można wyznaczyć metodami analizy. Mając wyznaczone te elementy możemy narysować wykres i odczytać z niego zbiór wartości funkcji.