Badanie monotoniczności funkcji za pomocą pochodnej

Drukuj

Poziom rozszerzony

Monotoniczność funkcji już omawiałem na tej stronie.
Przypomnijmy, że funkcja jest monotoniczna, jeżeli jest rosnąca, malejąca, niemalejąca, nierosnąca albo stała.

Twierdzenie

Niech funkcja \(f\) ma pochodną w przedziale \((a,b)\).
Jeżeli dla każdego \(x\in (a,b)\):

\(f'(x)\gt 0\), to \(f\) jest rosnąca w \((a,b)\),
\(f'(x)\lt 0\), to \(f\) jest malejąca w \((a,b)\),
\(f'(x)= 0\), to \(f\) jest stała w \((a,b)\).

Powyższe twierdzenie będzie zachodzić (dla przypadku funkcji rosnącej i malejącej) również w sytuacji, gdy dla skończonej liczby argumentów pochodna będzie przyjmowała wartość \(0\).

Zbadaj monotoniczność funkcji \(f(x)=(x-1)(x-3)\).

Wyznaczamy postać ogólną funkcji: \[f(x)=(x-1)(x-3)=x^2-4x+3\] Liczymy pochodną: \[f'(x)=2x-4\] Szukamy miejsc zerowych pochodnej: \[2x-4=0\\[6pt] x=2\] Rysujemy wykres pochodnej (dodatkowo na tym samym rysunku przedstawiłem wykres funkcji \(f(x)\), aby było łatwo zobaczyć, że dla argumentu w którym pochodna zmienia znak, jednocześnie funkcja zmienia monotoniczność):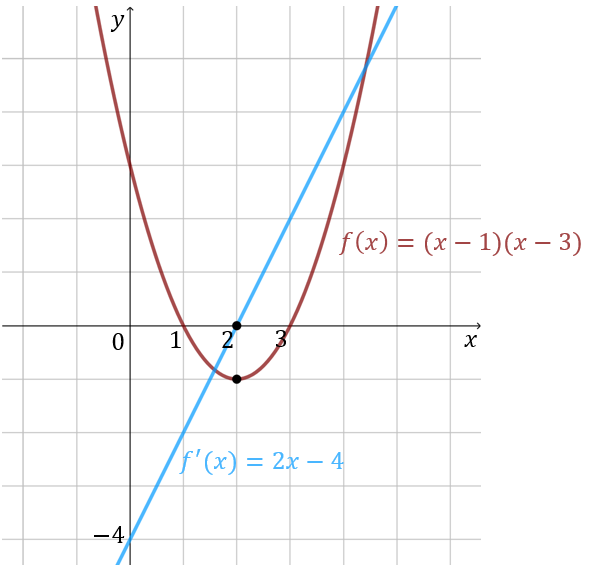

Badamy znak pochodnej:

\(f'(x)\gt 0\) dla \(x\gt2\). Zatem \(f(x)\) jest rosnąca dla \(x\in \langle 2; +\infty ) \).
\(f'(x)\lt 0\) dla \(x\lt 2\), zatem \(f(x)\) jest malejąca dla \(x\in(-\infty ;2\rangle \).

Dla argumentu \(x=2\) zmienia się znak pochodnej \(f'(x)\), zatem zmienia się też monotoniczność funkcji \(f(x)\).
Przy określaniu przedziałów monotoniczności argument \(x=2\) można zaliczać zarówno do przedziału w którym funkcja rośnie, jak i do przedziału w którym funkcja maleje.

Zbadaj monotoniczność funkcji \(f(x)=2x^3-x^4\).

Liczymy pochodną: \[f'(x)=6x^2-4x^3\] Szukamy miejsc zerowych pochodnej: \[6x^2-4x^3=0\\[6pt] 2x^2(3-2x)=0\\[6pt] x=0\quad \lor \quad x=\frac{3}{2}\] Rysujemy wykres pochodnej (dodatkowo na tym samym rysunku przedstawiłem wykres funkcji \(f(x)\), którego w tej chwili nie musimy jeszcze umieć rysować):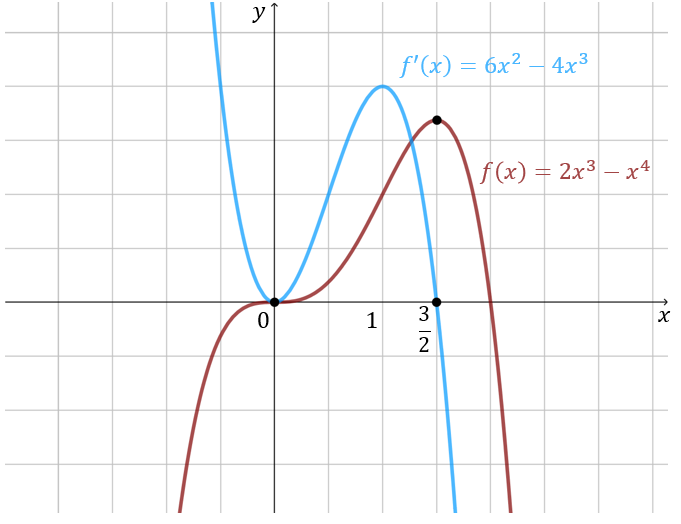

Z wykresu pochodnej widzimy, że:

\(f'(x)\gt 0\) dla \(x\in (-\infty ;0)\cup \left(0; \frac{3}{2}\right)\) oraz \(f'(0)=0\). Zatem \(f(x)\) jest rosnąca dla \(x\in \left(-\infty ; \frac{3}{2}\right\rangle \).
\(f'(x)\lt 0\) dla \(x\gt \frac{3}{2}\), zatem \(f(x)\) jest malejąca dla \(x\in \left\langle \frac{3}{2}; +\infty \right)\).

Zauważmy, że wyzerowanie pochodnej dla \(x=0\) nie popsuło monotoniczności na przedziale \(\left(-\infty ; \frac{3}{2}\right\rangle\).

Zależność między znakiem pochodnej a monotonicznością zachodzi również w drugą stronę, o czym mówi poniższe twierdzenie.

Twierdzenie

Niech funkcja \(f\) ma pochodną w przedziale \((a,b)\).

Jeżeli funkcja \(f\) jest rosnąca w \((a,b)\), to \(f'(x)\ge 0\) dla każdego \(x\in (a,b)\),
Jeżeli funkcja \(f\) jest malejąca w \((a,b)\), to \(f'(x)\le 0\) dla każdego \(x\in (a,b)\),

Funkcja \(f\), której dziedziną jest zbiór wszystkich liczb rzeczywistych, jest określona wzorem \(f(x)=-2x^3+3x^2\). Funkcja \(f\) jest rosnąca w przedziale

A.\( (-\infty ;0\rangle \)

B.\( \langle 0;1\rangle \)

C.\( \left\langle 1;\frac{3}{2} \right\rangle \)

D.\( \left\langle \frac{3}{2};+\infty \right) \)

Wykaż, że równanie \(2x^3-3x^2-5=0\) ma w przedziale \((2,3)\) dokładnie jedno rozwiązanie.

Wielomian \(f\) jest dany wzorem \(f(x)=3x^4-4kx^3+6x^2-12kx\) z parametrem rzeczywistym \(k\). Wyznacz wszystkie wartości \(k\), dla których funkcja \(f\) jest rosnąca w przedziale \(\langle 2;+\infty )\) i nie jest rosnąca w żadnym przedziale postaci \(\langle a;+\infty )\) dla \(a\lt 2\).

\(k=2\)

Funkcja \(f(x)=12x-x^3\) jest określona dla wszystkich liczb rzeczywistych. W przedziale \(\langle -1,1\rangle \) funkcja \(f\)

A.jest rosnąca.

B.jest malejąca.

C.ma dokładnie jedno ekstremum lokalne.

D.ma dokładnie dwa ekstrema lokalne.

Funkcja \(f(x)=2x^3-\frac{1}{2}x+1\) jest malejąca w przedziale

A.\( \left(-\infty ; -\frac{\sqrt{3}}{6}\right\rangle \)

B.\( (-\infty ; 0\rangle \)

C.\( \left\langle -\frac{\sqrt{3}}{6}; \frac{\sqrt{3}}{6}\right\rangle \)

D.\( \left\langle \frac{\sqrt{3}}{6}; +\infty \right ) \)