Zadania optymalizacyjne
Poziom rozszerzony
W zadaniach optymalizacyjnych zazwyczaj musimy: Wyznaczyć wzór funkcji \(f(x)\) opisującej sytuację z zadania oraz dziedzinę na której będziemy ją rozważali.
Obliczyć pochodną \(f'(x)\).
Wyznaczyć ekstrema lokalne funkcji \(f(x)\).
Wskazać ekstremum dla którego funkcja \(f(x)\) osiąga wartość największą lub najmniejszą i ewentualnie obliczyć tę wartość.
Zadania optymalizacyjne polegające na analizowaniu funkcji kwadratowej znajdziesz na stronie: Zadania optymalizacyjne z funkcji kwadratowej.
Okno na poddaszu ma kształt trapezu równoramiennego, którego krótsza podstawa i ramiona mają długość po \(4\) dm. Oblicz, jaką długość powinna mieć dłuższa podstawa tego trapezu, aby do pomieszczenia wpadało przez to okno jak najwięcej światła, czyli aby pole powierzchni okna było największe. Oblicz to pole.
Rozpatrujemy wszystkie trapezy równoramienne, w które można wpisać okrąg, spełniające warunek: suma długości dłuższej podstawy \(a\) i wysokości trapezu jest równa \(2\).
Wyznacz wszystkie wartości \(a\), dla których istnieje trapez o podanych własnościach.
Wykaż, że obwód \(L\) takiego trapezu, jako funkcja długości \(a\) dłuższej podstawy trapezu, wyraża się wzorem \(L(a) = \frac{4a^2 - 8a + 8}{a}\).
Oblicz tangens kąta ostrego tego spośród rozpatrywanych trapezów, którego obwód jest najmniejszy.
Funkcja \(f\) jest określona wzorem \(f(x) = 81^{\log_3x}+\frac{2\cdot \log_2\sqrt{27}\cdot \log_32}{3}\cdot x^2-6x\) dla każdej liczby dodatniej \(x\).
Wykaż, że dla każdej liczby dodatniej \(x\) wyrażenie \[81^{\log_3x}+\frac{2\cdot \log_2\sqrt{27}\cdot \log_32}{3}\cdot x^2-6x\] można równoważnie przekształcić do postaci \(x^4+x^2-6x\).
Oblicz najmniejszą wartość funkcji \(f\) określonej dla każdej liczby dodatniej \(x\). Zapisz obliczenia.
Wskazówka: przyjmij, że wzór funkcji \(f\) można przedstawić w postaci \(f(x) = x^4 + x^2 - 6x\).
W okrąg o promieniu \(R\) wpisano prostokąt \(ABCD\). Wyznacz możliwie największe pole tego prostokąta.
Rozpatrujemy wszystkie stożki, których przekrojem osiowym jest trójkąt o obwodzie \(20\). Oblicz wysokość i promień podstawy tego stożka, którego objętość jest największa. Oblicz objętość tego stożka.
Odcinek łączący środki dwóch skośnych krawędzi podstaw graniastosłupa prawidłowego czworokątnego ma długość \(10\). Jaką wysokość powinien mieć ten graniastosłup, aby pole jego powierzchni bocznej było maksymalne?
Wśród wszystkich graniastosłupów prawidłowych trójkątnych, w których suma długości wszystkich krawędzi jest równa \(12\), jest taki, który ma największą objętość. Oblicz długości krawędzi tego graniastosłupa i jego objętość.
W graniastosłupie prawidłowym trójkątnym suma długości trzech różnych krawędzi wychodzących z jednego wierzchołka wynosi \(S\). Wyznacz objętość tego graniastosłupa jako funkcję długości jednej z jego krawędzi i podaj dziedzinę tej funkcji. Oblicz wymiary graniastosłupa, którego objętość jest największa. Oblicz tę objętość.
Rozważmy wszystkie graniastosłupy prawidłowe trójkątne o objętości \(V = 2\). Wyznacz długości krawędzi tego z rozważanych graniastosłupów, którego pole powierzchni całkowitej jest najmniejsze. Oblicz to najmniejsze pole.
Rozważmy wszystkie ostrosłupy prawidłowe sześciokątne, w których suma długości krótszej przekątnej podstawy i wysokości ostrosłupa jest równa \(9\). Wyznacz długość krawędzi podstawy tego z rozważanych ostrosłupów, którego objętość jest największa. Oblicz tę największą objętość.
Rozpatrujemy wszystkie walce o danym polu powierzchni całkowitej \(P\). Oblicz wysokość i promień podstawy tego walca, którego objętość jest największa. Oblicz tę największą objętość.
Wyznacz promień podstawy stożka o tworzącej długości \(5\), którego objętość jest największa.
Parabola o równaniu \(y=2-\frac{1}{2}x^2\) przecina oś \(Ox\) układu współrzędnych w punktach \(A=(-2,0)\) i \(B=(2,0)\). Rozpatrujemy wszystkie trapezy równoramienne \(ABCD\), których dłuższą podstawą jest odcinek \(AB\), a końce \(C\) i \(D\) krótszej podstawy leżą na paraboli (zobacz rysunek). Wyznacz pole trapezu \(ABCD\) w zależności od pierwszej współrzędnej wierzchołka \(C\). Oblicz współrzędne wierzchołka \(C\) tego z rozpatrywanych trapezów, którego pole jest największe. 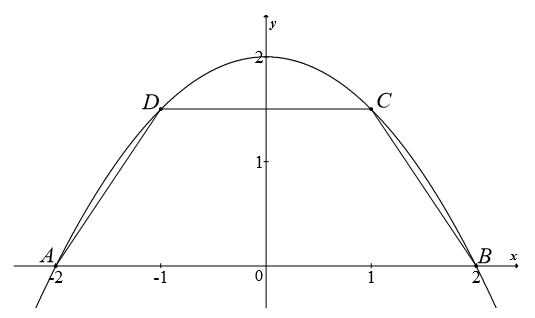

Tematy nadrzędne i sąsiednie