Ciągłość funkcji
Intuicyjnie powiemy, że funkcja jest ciągła jeżeli dla każdego argumentu \(x\) ze swojej dziedziny jej wykres jest nieprzerwany. Analogicznie definiujemy ciągłość funkcji w przedziałach typu \(\langle a,b)\), \((a,b\rangle \), \(\langle a, +\infty )\) oraz \((-\infty , a\rangle \).
Poniżej wykresy trzech funkcji nieciągłych w jednym punkcie oraz jednej funkcji ciągłej.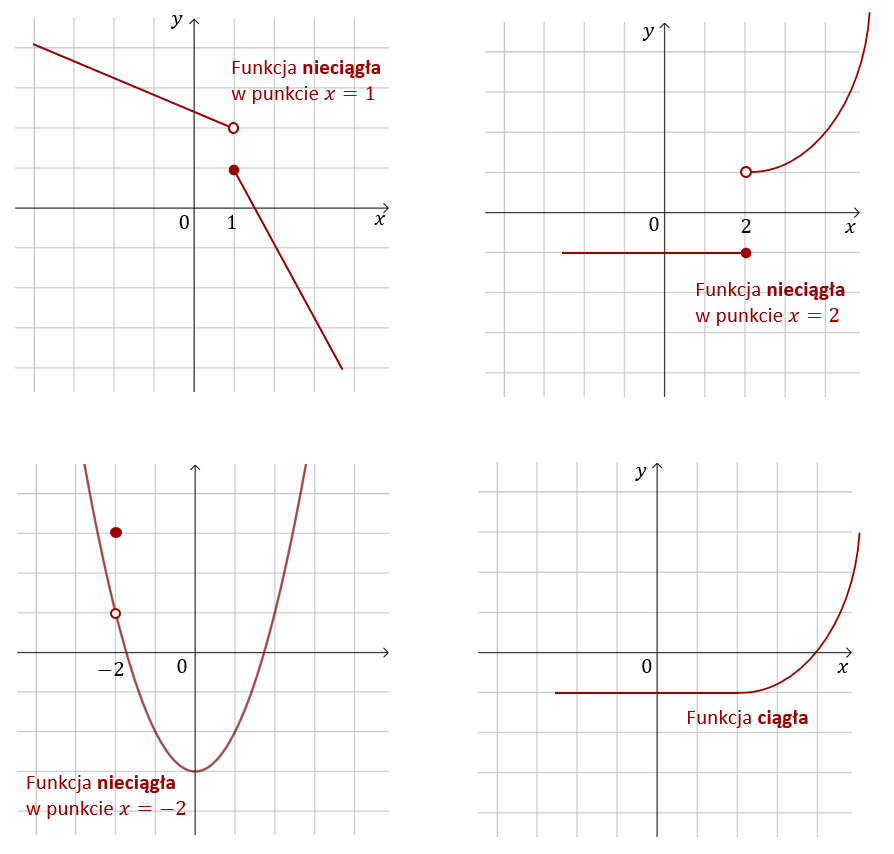 
Ważna uwaga! Ciągłość funkcji rozpatrujemy tylko w punktach należących do dziedziny tej funkcji! Zauważmy, że w powyższych przykładach funkcje zawsze były określone w punktach nieciągłości.
A teraz formalna definicja: Definicja ciągłości funkcji w punkcie
Funkcja \(f(x)\) określona w przedziale \((a, b)\) jest ciągła w punkcie \(x_0\in (a,b)\) wtedy i tylko wtedy, gdy istnieje granica \(\lim_{x \to x_0}f(x)\) oraz \(f(x_0)=\lim_{x \to x_0}f(x) \).
Funkcja \(f(x)=x^2-4\) jest ciągła w każdym punkcie swojej dziedziny. Na przykład w punkcie \(x_0=5\) funkcja \(f(x)\) jest ciągła, ponieważ: \[f(x_0)=f(5)=5^2-4=21\] oraz \[\lim_{x \to x_0}f(x)=\lim_{x \to 5}(x^2-4)=5^2-4=21\]
Wykaż, że funkcja \(f(x)=\begin{cases} x^2-3\ \text{dla } x\le1 \\ \frac{1}{3}x - \frac{7}{3}\ \text{dla } x\gt 1 \end{cases} \) jest ciągła w punkcie \(x_0=1\).
Obliczamy granice jednostronne funkcji w punkcie \(x_0=1\): \[\lim_{x \to x_0^-}f(x) = \lim_{x \to 1^-}(x^2-3)=1^2-3=-2\] oraz \[\lim_{x \to x_0^+}f(x) = \lim_{x \to 1^+}\left(\frac{1}{3}x - \frac{7}{3}\right)=\frac{1}{3}-\frac{7}{3}=-2\] Granica lewostronna i prawostronna są równe, zatem istnieje granica: \[\lim_{x \to x_0}f(x) = -2\] Teraz obliczamy wartość funkcji w punkcie \(x_0=1\): \[f(x_0)=f(1)=1^2-3=-2\] Zatem: \[\lim_{x \to x_0}f(x) = f(x_0)\] czyli \(f(x)\) jest ciągła w punkcie \(x_0\).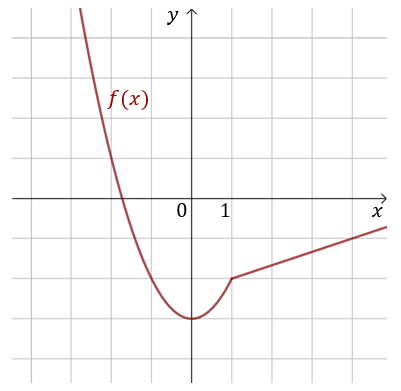 
Zbadaj ciągłość funkcji \(f(x)=\begin{cases} x^2-3\ \text{dla } x\le1 \\ \frac{1}{3}x +1\ \text{dla } x\gt 1 \end{cases} \) w punkcie \(x_0=1\).
Obliczamy granice jednostronne funkcji w punkcie \(x_0=1\): \[\lim_{x \to x_0^-}f(x) = \lim_{x \to 1^-}(x^2-3)=1^2-3=-2\] oraz \[\lim_{x \to x_0^+}f(x) = \lim_{x \to 1^+}\left(\frac{1}{3}x +1\right)=\frac{1}{3}+1=\frac{4}{3}\] Granica lewostronna i prawostronna są różne, zatem granica \(\lim_{x \to x_0}f(x)\) nie istnieje.
Zatem \(f(x)\) nie jest ciągła w punkcie \(x_0\).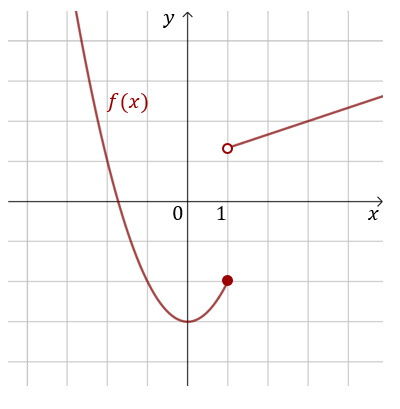
Zatem \(f(x)\) nie jest ciągła w punkcie \(x_0\).
Definicja funkcji ciągłej
Funkcję \(f(x)\) nazywamy funkcją ciągłą jeżeli jest ciągła w każdym punkcie swojej dziedzinie.
Jeżeli dziedziną funkcji jest zbiór będący sumą przedziałów, to powiemy, że funkcja jest ciągła, jeżeli jest ciągła w każdym z tych przedziałów.
Funkcja \(f(x)=\frac{1}{x}\) określona na zbiorze \((-\infty ; 0)\cup (0; +\infty )\) jest ciągła, ponieważ jest ciągła w każdym z przedziałów \((-\infty ; 0)\) oraz \((0; +\infty )\).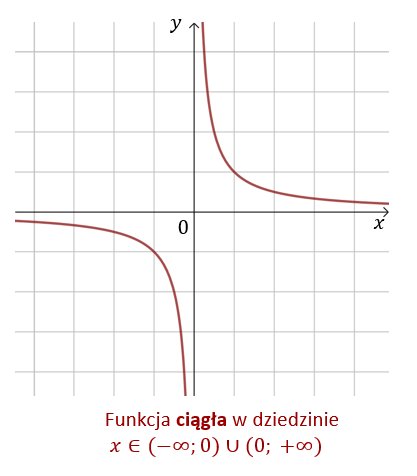 
W tego typu przykładach należy bardzo uważać przy określaniu ciągłości funkcji. Intuicyjnie można powiedzieć, że funkcja homograficzna \(f(x)=\frac{1}{x}\) jest nieciągła w punkcie \(x=0\), ale tak nie jest, ponieważ argument \(x=0\) nie należy do dziedziny tej funkcji.
Poniżej podam jeszcze kilka innych przykładów tego typu.
W tego typu przykładach należy bardzo uważać przy określaniu ciągłości funkcji. Intuicyjnie można powiedzieć, że funkcja homograficzna \(f(x)=\frac{1}{x}\) jest nieciągła w punkcie \(x=0\), ale tak nie jest, ponieważ argument \(x=0\) nie należy do dziedziny tej funkcji.Poniżej podam jeszcze kilka innych przykładów tego typu.
W tym przykładzie wykorzystałem wykresy funkcji z przykładu 1. i zmieniłem ich dziedziny w taki sposób, aby otrzymać funkcje ciągłe.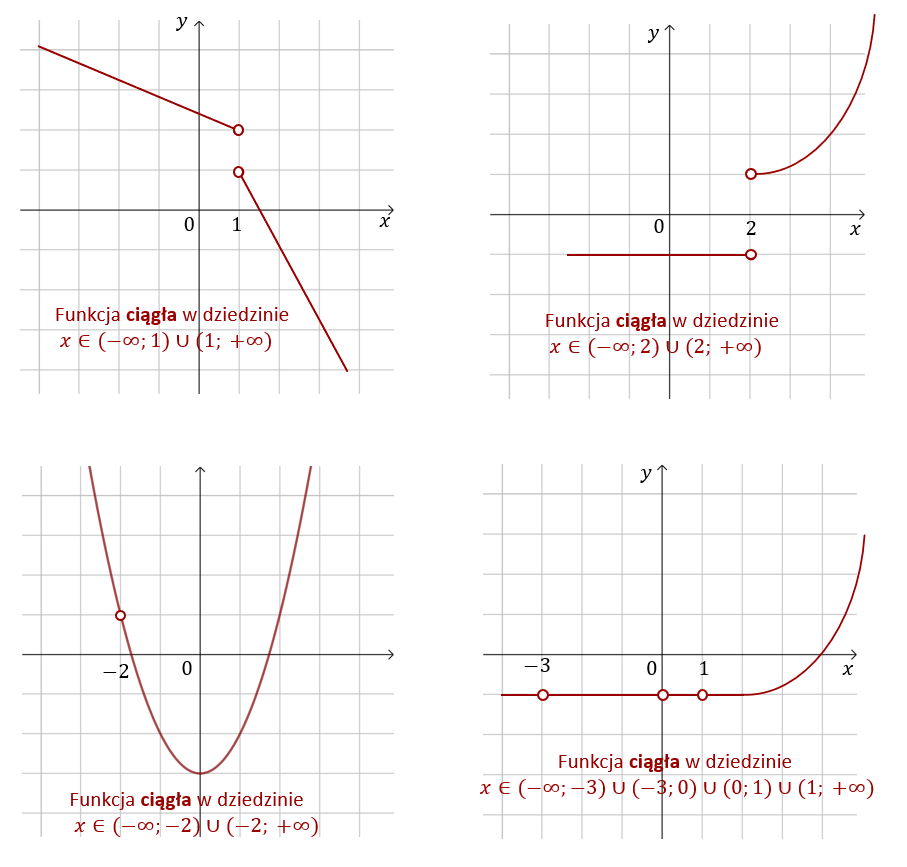 
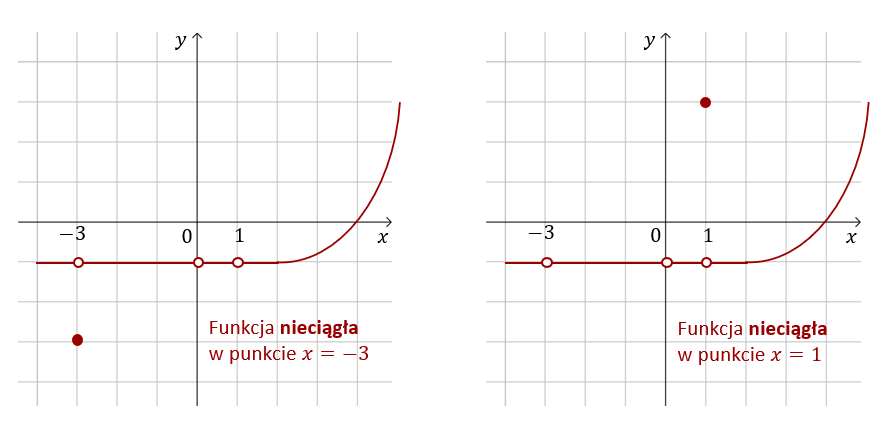
Z ostatniej funkcji można łatwo zrobić funkcję nieciągłą. Wystarczy dodać do dziedziny przynajmniej jeden z argumentów: \(-3\), \(0\) lub \(1\). 
Z ostatniej funkcji można łatwo zrobić funkcję nieciągłą. Wystarczy dodać do dziedziny przynajmniej jeden z argumentów: \(-3\), \(0\) lub \(1\). Definicja funkcji ciągłej w przedziale domkniętym
Funkcję \(f(x)\) jest ciągła w przedziale \(\langle a, b \rangle \) jeżeli jest ciągła w \((a,b)\) oraz \[\lim_{x \to a^+} f(x)=f(a) \ \ \text{i} \ \ \lim_{x \to b^-} f(x)=f(b)\]
Funkcja \(f(x)=\sqrt{x}\) jest określona dla \(x\in \langle 0; +\infty )\).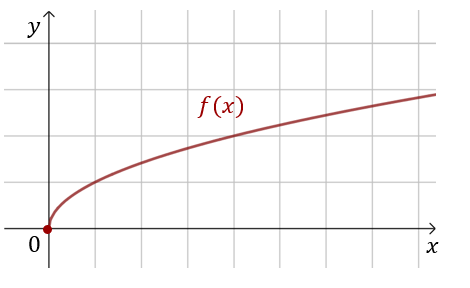 
Dla punktu \(x=0\) mamy równość: \[\lim_{x \to 0^+} f(x)=f(0)\] Zatem funkcja \(f(x)\) jest ciągła w całej dziedzinie.
Dla punktu \(x=0\) mamy równość: \[\lim_{x \to 0^+} f(x)=f(0)\] Zatem funkcja \(f(x)\) jest ciągła w całej dziedzinie. W filmie omawiam definicję ciągłości funkcji i pokazuję kilkanaście przykładów funkcji ciągłych i nieciągłych.
Czas nagrania: 27 min.