Styczna do wykresu funkcji
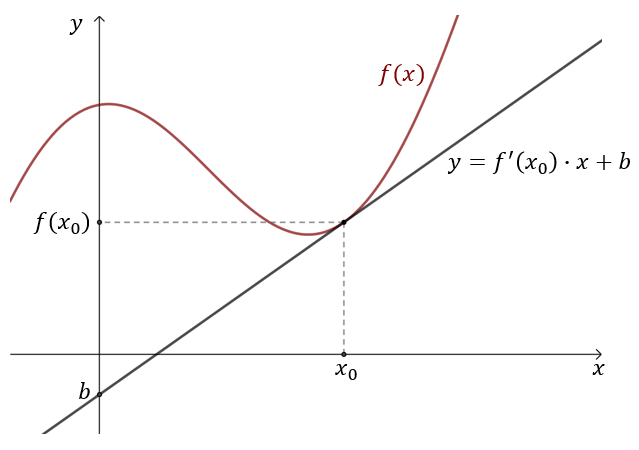
Prosta styczna do wykresu funkcji \(f(x)\) w punkcie \((x_0, f(x_0))\) wyraża się wzorem: \[y=f'(x_0)(x-x_0)+f(x_0)\] Współczynnik kierunkowy prostej stycznej, to \(f'(x_0)\). 
Równanie prostej stycznej zapisane w postaci kierunkowej, to: \[y=f'(x_0)\cdot x+b\] gdzie \(b=f(x_0)-f'(x_0)\cdot x_0\).
Wskazówka
Przy wyznaczaniu równania prostej stycznej kluczowe jest obliczenie \(f'(x_0)\). Wzoru na \(b\) nie ma sensu zapamiętywać, ponieważ \(b\) wyliczamy podstawiając współrzędne punktu \((x_0,f(x_0))\) do równania \(y=f'(x_0)\cdot x+b\) odpowiednio pod \(x\) oraz \(y\). W ten sposób można też wyprowadzić wzór na \(b=f(x_0)-f'(x_0)\cdot x_0\). Wyznacz równanie stycznej do wykresu funkcji \(f(x)=x^2-2x+1\) w punkcie \(x_0=3\).
Liczymy pochodną funkcji: \[f'(x)=2x-2\] Zatem: \[f'(x_0)=f'(3)=2\cdot 3-2=4\] Wyznaczamy równanie prostej stycznej: \[\begin{split} y&=f'(x_0)\cdot x+b\\[6pt] y&=4x+b \end{split}\] Żeby obliczyć współczynnik \(b\) podstawimy do równania prostej stycznej współrzędne punktu \((x_0,f(x_0))\), który należy do tej prostej.
Obliczamy: \[f(x_0)=f(3)=3^2-2\cdot 3+1=4\] Czyli punkt \((x_0,f(x_0)) = (3,4)\). Zatem podstawiamy: \[\begin{split} y&=4x+b\\[6pt] 4&=4\cdot 3+b\\[6pt] b&=-8 \end{split}\] Zatem równanie prostej stycznej do funkcji \(f(x)=x^2-2x+1\) w punkcie \(x_0=3\) jest postaci: \[y=4x-8\]
Obliczamy: \[f(x_0)=f(3)=3^2-2\cdot 3+1=4\] Czyli punkt \((x_0,f(x_0)) = (3,4)\). Zatem podstawiamy: \[\begin{split} y&=4x+b\\[6pt] 4&=4\cdot 3+b\\[6pt] b&=-8 \end{split}\] Zatem równanie prostej stycznej do funkcji \(f(x)=x^2-2x+1\) w punkcie \(x_0=3\) jest postaci: \[y=4x-8\]
Funkcja \(f\) jest określona wzorem \(f(x)=\frac{x-1}{x^2+1}\) dla każdej liczby rzeczywistej \(x\). Wyznacz równanie stycznej do wykresu tej funkcji w punkcie \(P=(1,0)\).
Wykaż, że nie istnieje styczna do hiperboli o równaniu \(y=\frac{4x}{x-3}\) prostopadła do prostej \(l\) o równaniu \(2x+4y-1=0\).
Funkcja \(f\) określona jest wzorem \(f(x)=x^3-2x^2+1\) dla każdej liczby rzeczywistej \(x\). Wyznacz równania tych stycznych do wykresu funkcji \(f\), które są równoległe do prostej o równaniu \(y=4x\).
Funkcja \(f\) określona jest wzorem \(f(x)=x^3-4x\). Prosta o równaniu \(x=1\) przecina wykres funkcji \(f\) w punkcie \(P\). Znajdź równanie stycznej do wykresu funkcji \(f\) w punkcie \(P\).