Największa i najmniejsza wartość funkcji w przedziale
Poziom rozszerzony
Ekstrema na przedziale domkniętym
Funkcja ciągła \(f\) na przedziale domkniętym \(\langle a,b\rangle \) osiąga w tym przedziale wartość największą oraz najmniejszą.Wartości ekstremalne mogą być przyjmowane:
- na krańcach przedziałów (wtedy wartość największa/najmniejsza jest równa\(f(a)\) albo \(f(b)\)),
- albo dla argumentu \(x\) dla którego pochodna \(f'(x)\) zmienia znak.
Wyznacz wartości ekstremalne funkcji \(f(x)=(x-1)(x-3)\) na przedziale \(\langle -1; 4 \rangle \).
Wartość największa funkcji to: \(f(-1)=8\), a wartość najmniejsza to: \(f(2)=-1\).
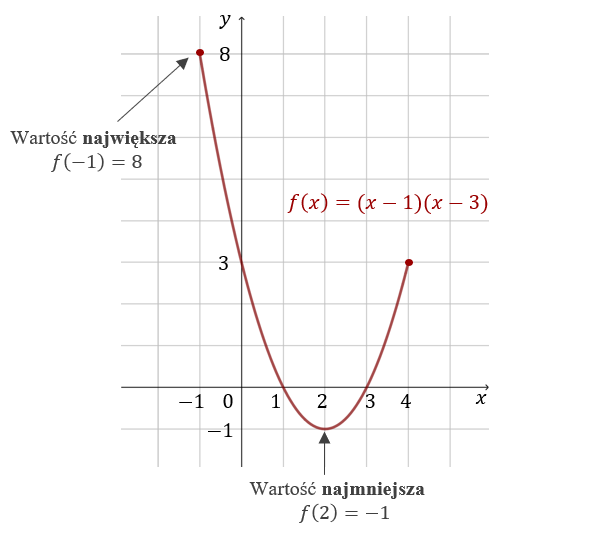
Wyznaczamy wierzchołek funkcji kwadratowej: \[W=(2,-1)\] i sprawdzamy, że należy do podanego przedziału \(\langle -1; 4 \rangle \).
Wyznaczamy wartości funkcji na krańcach przedziału: \[f(-1)=8\] \[f(4)=3\] Spośród otrzymanych trzech wartości (\(-1,\ 8\) oraz \(3\)) wybieramy największą i najmniejszą.Wartość największa funkcji to: \(f(-1)=8\), a wartość najmniejsza to: \(f(2)=-1\).
Wyznacz wartości ekstremalne funkcji \(f(x)=x^3-\frac{3}{2}x^2-6x+1\) na przedziale \(\langle -2; 4 \rangle \).
Liczymy pochodną funkcji: \[f'(x)=3x^2-3x-6\] Szukamy miejsc zerowych pochodnej: \[ 3x^2-3x-6=0\\[6pt] 3(x^2-x-2)=0\\[6pt] 3(x+1)(x-2)=0\\[6pt] x=-1\quad \lor \quad x=2 \] Badamy zmianę znaku pochodnej w miejscach zerowych: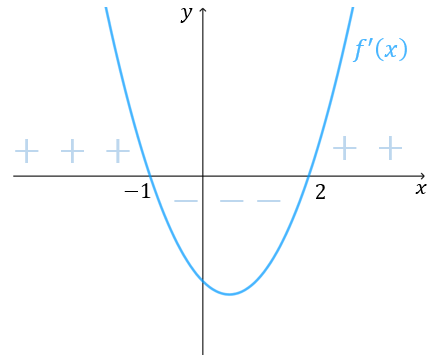 
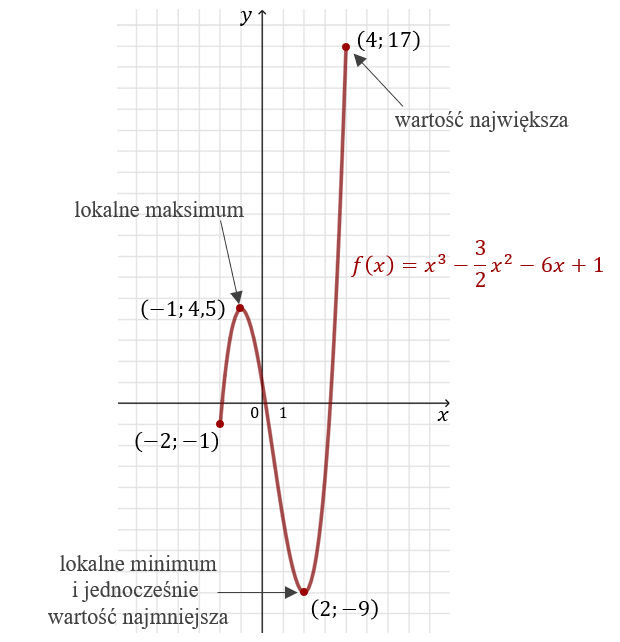
Zatem dla \(x=-1\) funkcja \(f(x)\) przyjmuje maksimum lokalne: \[f(-1)=-1-\frac{3}{2}+6+1=4{,}5\] A dla \(x=2\) funkcja \(f(x)\) przyjmuje minimum lokalne: \[f(2)=8-6-12+1=-9\] Sprawdzamy jeszcze wartości funkcji na krańcach przedziałów: \[f(-2)=-8-6+12+1=-1\] oraz: \[f(4)=64-24-24+1=17\] Zatem ostatecznie na przedziale domkniętym \(\langle -2; 4 \rangle \) funkcja \(f(x)\) przyjmuje wartość największą równą 17 dla \(x=4\) oraz wartość najmniejszą równą \(-9\) dla \(x=2\). 
Zatem dla \(x=-1\) funkcja \(f(x)\) przyjmuje maksimum lokalne: \[f(-1)=-1-\frac{3}{2}+6+1=4{,}5\] A dla \(x=2\) funkcja \(f(x)\) przyjmuje minimum lokalne: \[f(2)=8-6-12+1=-9\] Sprawdzamy jeszcze wartości funkcji na krańcach przedziałów: \[f(-2)=-8-6+12+1=-1\] oraz: \[f(4)=64-24-24+1=17\] Zatem ostatecznie na przedziale domkniętym \(\langle -2; 4 \rangle \) funkcja \(f(x)\) przyjmuje wartość największą równą 17 dla \(x=4\) oraz wartość najmniejszą równą \(-9\) dla \(x=2\). Wyznacz największą i najmniejszą wartość funkcji \(f\) na danym przedziale.
\(f(x)=\frac{x^3}{3}-4x\), \(x\in \langle -1; 3 \rangle \)
\(f(x)=x^2-\frac{4x}{1-x}\), \(x\in (1; 3 \rangle \)
\(f(x)=x^3+3x^2+3x-5\), \(x\in \langle -2; 1 \rangle \)
Funkcja \(f(x)=12x-x^3\) jest określona dla wszystkich liczb rzeczywistych. W przedziale \(\langle -1,1\rangle \) funkcja \(f\)
A.jest rosnąca.
B.jest malejąca.
C.ma dokładnie jedno ekstremum lokalne.
D.ma dokładnie dwa ekstrema lokalne.
Funkcja wymierna \(f\) jest dana wzorem \(f(x)=\frac{x+1}{x^2+2x+2}\). Wyznacz wartość najmniejszą i wartość największą, jakie ta funkcja przyjmuje dla argumentów z przedziału \(\langle -3,1 \rangle \)
Tematy nadrzędne i sąsiednie