Funkcja kwadratowa
1.
Zestawienie najważniejszych wzorów i własnościZestawienie najważniejszych wzorów i własności
Poziom podstawowy
W tym miejscu zebrałem wszystkie najważniejsze wzory dotyczące funkcji kwadratowej. - Postać ogólna funkcji kwadratowej to: \[f(x)=a x^2+b x+c\] gdzie \(a, b, c \in \mathbb{R}\) i \(a \neq 0\).
- Wyróżnik \(\Delta\) (delta) trójmianu kwadratowego \(ax^2+bx+c\), to liczba: \[\Delta=b^2-4ac\]
- Miejsca zerowe funkcji kwadratowej \(f(x)=a x^2+b x+c\), to rozwiązania rzeczywiste równania kwadratowego: \[a x^2+b x+c=0\] Jeżeli \(\Delta\gt 0\), to są dwa rozwiązania (miejsca zerowe): \[x_1=\frac{-b-\sqrt{\Delta}}{2 a} \quad \text{i} \quad x_2=\frac{-b+\sqrt{\Delta}}{2 a}\] Jeżeli \(\Delta= 0\), to jest dokładnie jedno rozwiązanie (miejsce zerowe): \[x_1=x_2=-\frac{b}{2 a}\] Jeżeli \(\Delta\lt 0\), to nie ma rozwiązań (miejsc zerowych).
- Wykresem funkcji kwadratowej jest parabola o wierzchołku w punkcie \(W=(p, q)\), gdzie: \[p=-\frac{b}{2a}\] \[q=-\frac{\Delta}{4a}\] Współrzędną \(q\) można też policzyć jako wartość funkcji od argumentu \(x=p\): \(q=f(p)\).
- Ramiona paraboli skierowane są do dołu jeżeli \(a\lt 0\). Ramiona paraboli skierowane są do góry dla \(a\gt 0\).
- Oś symetrii paraboli jest dana równaniem: \(x=p\).
- Punkt przecięcia paraboli z osią \(y\)-ów, który ma współrzędne \((0, c)\).
- Postać kanoniczna funkcji kwadratowej to: \[f(x)=a(x-p)^2+q\]
- Postać iloczynowa funkcji kwadratowej istnieje jeżeli \( \Delta \geqslant 0\) i ma wzór: \[f(x)=a\left(x-x_1\right)\left(x-x_2\right)\] gdzie \(x_1\) i \(x_2\) to miejsca zerowe funkcji kwadratowej.
- Wzory Viete'a
Jeżeli \(\Delta \geqslant 0\), to zachodzą wzory: \[x_1+x_2=-\frac{b}{a} \] \[x_1 \cdot x_2=\frac{c}{a}\]
Ilustracja powyższych zagadnień na przykładzie funkcji \(f(x)=x^2-4x-5\): 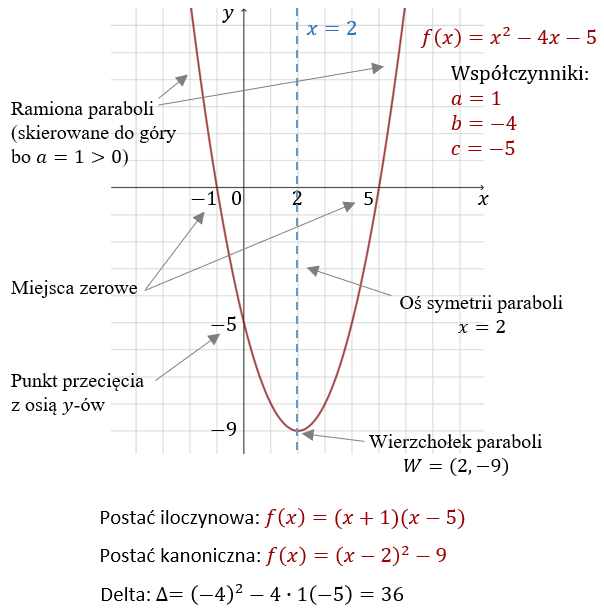

Kompleksowe omówienie funkcji kwadratowej:
- Podstawowe własności funkcji kwadratowej.
- Wyznaczanie wzoru funkcji kwadratowej.
- Postać kanoniczna, ogólna iloczynowa.
- Wierzchołek paraboli, miejsca zerowe i oś symetrii.
- Własności funkcji kwadratowej
- Równania i nierówności kwadratowe.
- Wyznaczanie największej i najmniejszej wartości funkcji kwadratowej w przedziale domkniętym.
- Zadania optymalizacyjne.
Czas lekcji: 100 min.
W tej lekcji wideo znajdziesz dokładne omówienie funkcji kwadratowej.
Czas lekcji: 45 min.
Tematy nadrzędne i sąsiednie