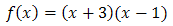Jesteś tutaj: Szkoła → Funkcja kwadratowa → Postać ogólna, kanoniczna i iloczynowa funkcji kwadratowej → Zamiana postaci kanonicznej na postać ogólną i iloczynową
Zamiana postaci kanonicznej na postać ogólną i iloczynową
Teraz pokażemy jak zamienić funkcję kwadratową zapisaną w postaci kanonicznej: \[f(x)=a(x-p)^2+q\] na postać ogólną oraz iloczynową.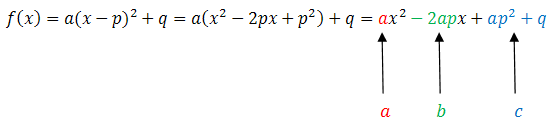 
Możemy zatem zapisać wzory na współczynniki liczbowe \(b\) i \(c\): \[\begin{split} &b=-2ap\\[6pt] &c=ap^2+q \end{split}\] Teraz gdy znamy współczynniki liczbowe \(a\), \(b\) i \(c\), to możemy zapisać wzór funkcji w postaci ogólnej: \[f(x)=ax^2+bx+c\]
Metoda zamiany postaci kanonicznej na ogólną
Żeby zamienić wzór funkcji kwadratowej na postać ogólną, to wystarczy podnieść nawias do kwadratu i uprościć wyrażenie: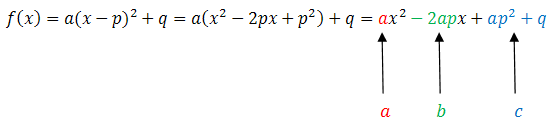 Możemy zatem zapisać wzory na współczynniki liczbowe \(b\) i \(c\): \[\begin{split} &b=-2ap\\[6pt] &c=ap^2+q \end{split}\] Teraz gdy znamy współczynniki liczbowe \(a\), \(b\) i \(c\), to możemy zapisać wzór funkcji w postaci ogólnej: \[f(x)=ax^2+bx+c\] W praktyce przekształcanie wzoru funkcji kwadratowej na postać ogólną jest bardzo proste i nie wymaga pamiętania żadnych wzorów. Przekonasz się o tym na poniższych przykładach. Wcześniej jednak omówimy metodę zamieniania postaci kanonicznej na iloczynową.
Metoda zamiany postaci kanonicznej na iloczynową
Aby zamienić wzór funkcji z postaci kanonicznej na postać iloczynową, to wystarczy obliczyć miejsca zerowe \(x_1\) i \(x_2\). Żeby to zrobić, to warto najpierw zamienić wzór funkcji na postać ogólną, a następnie obliczyć miejsca zerowe korzystając z delty i wzorów na \(x_1\) oraz \(x_2\).
Alternatywną metodą jest obliczenie miejsc zerowych wprost z postaci kanonicznej w następujący sposób: \[\begin{split} a(x-p)^2+q&=0\\[6pt] a(x-p)^2&=-q\\[6pt] (x-p)^2&=-\frac{q}{a}\\[6pt] x-p=\sqrt{-\frac{q}{a}}\quad &\lor \quad x-p=-\sqrt{-\frac{q}{a}}\\[6pt] x=p+\sqrt{-\frac{q}{a}}\quad &\lor \quad x=p-\sqrt{-\frac{q}{a}}\\[6pt] \end{split}\] Powyższy rachunek ma sens przy założeniu, że liczba \(-\frac{q}{a}\ge0\) (bo nie wolno wyciągać pierwiastka z liczby ujemnej). W przeciwnym przypadku miejsca zerowe nie istnieją.
Przekształć wzór funkcji \(f(x) = (x + 1)^2 - 4\) na postać ogólną i iloczynową.
Zaczynamy od wyznaczenia postaci ogólnej. W tym celu podnosimy nawias do kwadratu i upraszczamy wyrażenie:
Wypiszmy na początku współczynniki liczbowe \(a\), \(b\) i \(c\) wyznaczonej przed chwilą postaci ogólnej:
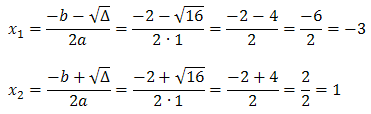Wyliczone wartości podstawiamy do wzoru na postać iloczynową: 
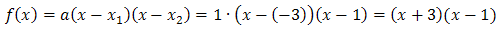Zatem ostatecznie postać iloczynowa funkcji kwadratowej jest następująca: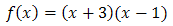 
\[f(x) = (x + 1)^2 - 4 = x^2 + 2x + 1 - 4 = x^2 + 2x - 3\]
Czyli postać ogólna jest następująca: \[f(x) = x^2 + 2x - 3\] Teraz wyznaczymy postać iloczynową. Musimy w tym celu wyliczyć miejsca zerowe \(x_1\) i \(x_2\).Wypiszmy na początku współczynniki liczbowe \(a\), \(b\) i \(c\) wyznaczonej przed chwilą postaci ogólnej:
\(a = 1\)
\(b = 2\)
\(c = -3\)
Obliczymy deltę: \(b = 2\)
\(c = -3\)
\[\Delta = b^2 - 4ac = 2^2 - 4\cdot 1\cdot (-3) = 4 + 12 = 16\]
Teraz obliczamy miejsca zerowe \(x_1\) i \(x_2\) korzystając z poznanych wzorów: 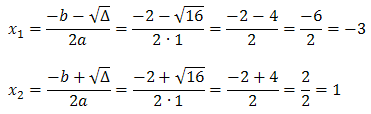Wyliczone wartości podstawiamy do wzoru na postać iloczynową: 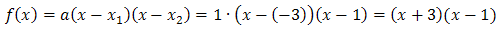Zatem ostatecznie postać iloczynowa funkcji kwadratowej jest następująca: