Wykres funkcji kwadratowej

Poziom podstawowy

W tym rozdziale podsumujemy i przypomnimy informacje z kilku poprzednich rozdziałów o funkcji kwadratowej.

Wykresem funkcji kwadratowej jest parabola.

Do narysowania paraboli warto ustalić:

Miejsca zerowe funkcji kwadratowej.
Dla funkcji danej w postaci ogólnej \(f(x)=ax^2+bx+c\) liczymy deltę \(\Delta=b^2-4ac\), a następnie:
Jeżeli \(\Delta\gt 0\), to są dwa miejsca zerowe: \[x_1=\frac{-b-\sqrt{\Delta}}{2 a} \quad \text{i} \quad x_2=\frac{-b+\sqrt{\Delta}}{2 a}\] Jeżeli \(\Delta= 0\), to jest dokładnie jedno miejsce zerowe: \[x_1=x_2=-\frac{b}{2 a}\] Jeżeli \(\Delta\lt 0\), to nie ma miejsc zerowych.
Parabola ma wierzchołek w punkcie \(W=(p, q)\), gdzie: \[p=-\frac{b}{2a}\qquad q=-\frac{\Delta}{4a}\] Współrzędną \(q\) można też policzyć jako wartość funkcji od argumentu \(x=p\): \(q=f(p)\).
Ramiona paraboli skierowane są do dołu jeżeli \(a\lt 0\). Ramiona paraboli skierowane są do góry jeżeli \(a\gt 0\).
Oś symetrii paraboli jest dana równaniem: \(x=p\).
Punkt przecięcia paraboli z osią \(y\)-ów ma współrzędne \((0, c)\).

Podsumowanie zagadnień na przykładzie funkcji \(f(x)=x^2-4x-5\):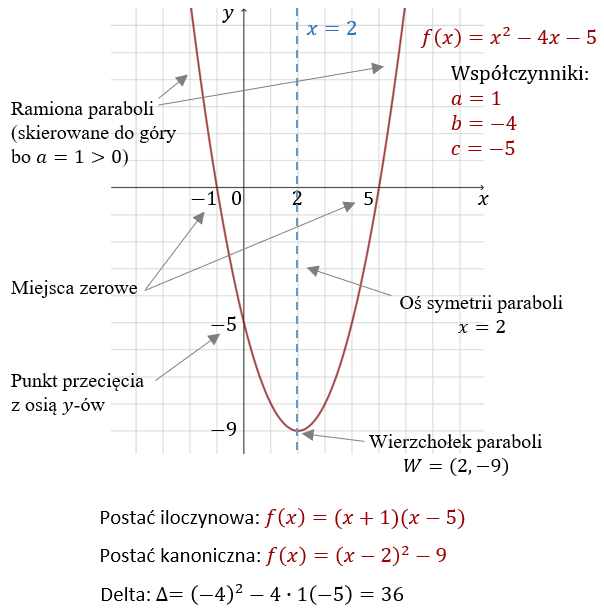

Narysuj wykres funkcji kwadratowej \(f(x) = x^2 - 2x - 8\) i omów jej własności.

Współczynniki liczbowe tej funkcji kwadratowej, to: \[a=1,\quad b=-2,\quad c=-8\]

Współczynnik \(a\) jest dodatni czyli ramiona paraboli są skierowane do góry.

Liczymy miejsca zerowe: \[\Delta =b^2-4ac=(-2)^2-4\cdot 1\cdot (-8)=4+32=36\] \[\begin{split} &x_1=\frac{-b-\sqrt{\Delta }}{2a}=\frac{2-6}{2}=-2\\[6pt] &x_2=\frac{-b+\sqrt{\Delta }}{2a}=\frac{2+6}{2}=4 \end{split}\]

Liczymy współrzędne wierzchołka: \[\begin{split} &p=\frac{-b}{2a}=\frac{2}{2}=1\\[6pt] &q=\frac{-\Delta }{4a}=\frac{-36}{4}=-9 \end{split}\] Czyli wierzchołek paraboli jest w punkcie \(W=(1,-9)\).

Liczymy punkt przecięcia paraboli z osią \(y\)-ów: \[f(0)=c=-8\] Czyli punkt przecięcia paraboli z osią \(y\)-ów ma współrzędne \((0,-8)\).

Zaznaczamy w układzie współrzędnych wyliczone punkty i rysujemy wykres: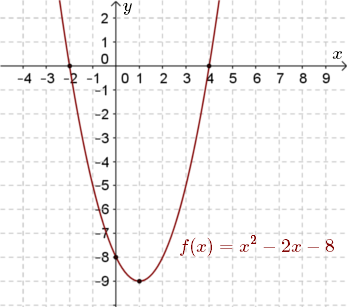

Teraz omówimy własności tej funkcji.

Dziedzina: \(\mathbb{R}\).
Zbiór wartości: \(\langle -9;+\infty )\).
Funkcja ma dwa miejsca zerowe: \(x_1 = -2\) oraz \(x_2 = 4\).
Funkcja ma wierzchołek w punkcie \(W=(1,-9)\).
Funkcja jest malejąca dla \(x\in (-\infty ,1\rangle \).
Funkcja jest rosnąca dla \(x\in \langle 1, +\infty )\).
Funkcja przecina oś y-ów w punkcie: \((0, -8)\).
Funkcja przyjmuje wartości dodatnie, gdy \(x\in (-\infty ; -2) \cup (4 +\infty )\).
Funkcja przyjmuje wartości ujemne, gdy \(x\in (-2; 4)\).
Oś symetrii paraboli to \(x=1\).

Wykres dowolnej funkcji, to możesz narysować za pomocą programu do rysowania wykresów.

Wskaż fragment wykresu funkcji kwadratowej, której zbiorem wartości jest \(\langle -2,+\infty )\).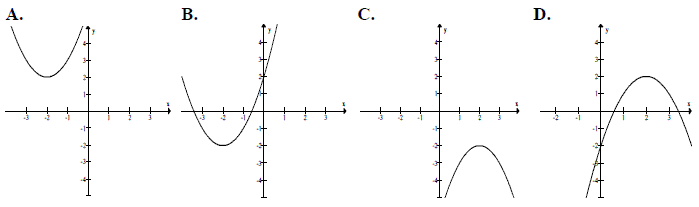

Na jednym z poniższych rysunków przedstawiono fragment wykresu funkcji \(y=x^2+2x-3\). Wskaż ten rysunek.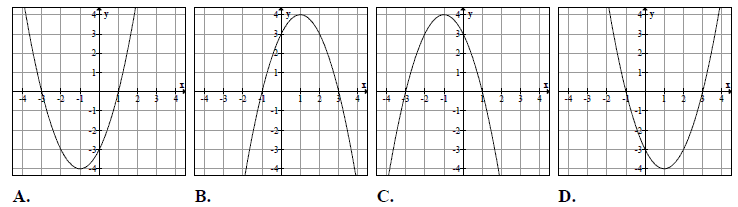

Na wykresie przedstawiony jest trójmian \(y = ax^2 + bx + c\).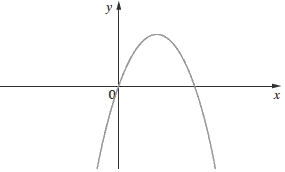

Wynika z tego, że:

A.\( b\lt 0 \)

B.\( b>0 \)

C.\( b\le 0 \)

D.\( b\ge 0 \)

Funkcja kwadratowa, której zbiorem wartości jest przedział \( ( -\infty, -3\rangle \) , może być określona wzorem

A.\(y=(x+2)^2-3 \)

B.\(y=-(x+3)^2 \)

C.\(y=-(x-2)^2-3 \)

D.\(y=-x^2+3 \)

W układzie współrzędnych narysowano część paraboli o wierzchołku w punkcie \( A=(2, 4) \), która jest wykresem funkcji kwadratowej \( f \).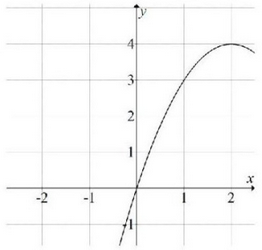

Funkcja \( f \) może być opisana wzorem

A.\(f(x)=(x-2)^2+4 \)

B.\(f(x)=(x+2)^2+4 \)

C.\(f(x)=-(x-2)^2+4 \)

D.\(f(x)=-(x+2)^2+4 \)

Dwie funkcje \(f(x)=2x-1\) oraz \(g(x)=-x^2\) określone są w zbiorze \(\mathbb{R}.\) Wówczas wykres funkcji \(h\) określonej wzorem \(h(x)=f(x)+g(x)\) jest przedstawiony na rysunku: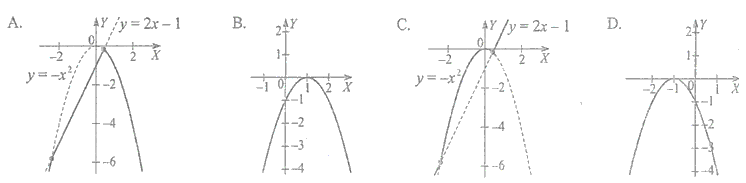

Wykres funkcji \(f(x)=x^2-2x-8,\) gdzie \(x \in \mathbb{R}\), przecina oś \(OX\) w punktach \(A\) i \(B\).

Wyznacz współrzędne punktów \(A\) i \(B\).
Oblicz pole trójkąta \(AWB\), jeśli \(W\) jest wierzchołkiem paraboli będącej wykresem funkcji \(f\).

\(A=(-2,0)\), \(B=(4,0)\), \(P_{\Delta AWB}=27\)

Wykres funkcji kwadratowej \(f\) określonej wzorem \(f(x)=ax^2+bx+c\) ma z prostą o równaniu \(y=6\) dokładnie jeden punkt wspólny. Punkty \(A=(-5,0)\) i \(B=(3,0)\) należą do wykresu funkcji \(f\). Oblicz wartości współczynników \(a\), \(b\) oraz \(c\).

\(a=-\frac{3}{8}\), \(b=-\frac{3}{4}\), \(c=\frac{45}{8}\)