Oś symetrii paraboli

Poziom podstawowy

Dla funkcji kwadratowej określonej wzorem: \[f(x)=ax^2+bx+c\] osi symetrii ma równanie: \[x=\frac{-b}{2a}\] Oś symetrii paraboli zawsze jest pionowa i przechodzi przez wierzchołek paraboli.

Wskaż równanie osi symetrii paraboli określonej równaniem \( y=-x^2+4x-11 \).

A.\(x=-4 \)

B.\(x=-2 \)

C.\(x=2 \)

D.\(x=4 \)

Osią symetrii wykresu funkcji kwadratowej \(f(x) = −2x^2 −8x + 6\) jest prosta o równaniu

A.\( y=2 \)

B.\( y=-2 \)

C.\( x=2 \)

D.\( x=-2 \)

Wskaż równanie prostej, która jest osią symetrii paraboli o równaniu \(\ y=x^2-4x+2010\).

A.\( x=4 \)

B.\( x=-4 \)

C.\( x=2 \)

D.\( x=-2 \)

Na rysunku przedstawiony jest fragment wykresu funkcji kwadratowej \(f\).

Osią symetrii paraboli jest prosta o równaniu \(x=-3\). Rozwiązaniem nierówności \(f(x)\le 0\) jest zbiór

A.\( \langle 0,-3\rangle \)

B.\( \langle -3,3\rangle \)

C.\( \langle -6,3\rangle \)

D.\( \langle -9,3\rangle \)

Wykresem funkcji kwadratowej \(f\) określonej wzorem \(f(x)=x^2+bx+c\) jest parabola, na której leży punkt \(A=(0,-5)\). Osią symetrii tej paraboli jest prosta o równaniu \(x=7\). Oblicz wartości współczynników \(b\) i \(c\).

\(b=-14\), \(c=-5\)

Dana jest funkcja \(f(x)=-3x^2+bx+c\) dla \(x\in \mathbb{R} \). Prosta o równaniu \(x=2\) jest osią symetrii paraboli będącej jej wykresem, a zbiorem wartości funkcji \(f\) jest przedział \((-\infty ;21\rangle \). Wyznacz współczynniki \(b\) i \(c\).

\(b=12, c=9\)

Osią symetrii wykresu funkcji kwadratowej \(f\) określonej wzorem \(f(x)= \frac{1}{3}x^2 + 4x + 7\) jest prosta o równaniu

A.\( x=-6 \)

B.\( y=-6 \)

C.\( x=-2 \)

D.\( y=-2 \)

Osią symetrii wykresu funkcji \(f\) jest prosta o równaniu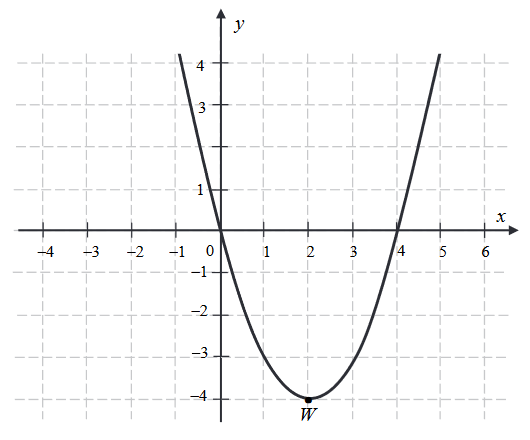

A.\( y = -4 \)

B.\( x = -4 \)

C.\( y = 2 \)

D.\( x = 2 \)

\(x = 2\)

Osią symetrii wykresu funkcji kwadratowej \(f(x)=\frac{1}{7}(x-5)(x+9)\) jest prosta o równaniu:

A.\( x=5 \)

B.\( x=-9 \)

C.\( x=-2 \)

D.\( x=-7 \)