Proste równoległe i prostopadłe
Poziom podstawowy
Dwie proste: \(y=a_1x+b_1\) oraz \(y=a_2x+b_2\) są:
- równoległe, jeżeli \(a_1=a_2\) (współczynniki kierunkowe są równe),
- prostopadłe, jeżeli \(a_1\cdot a_2=-1\) (lub równoważnie \(a_1=-\frac{1}{a_2}\)).
Współczynnik kierunkowy prostej równoległej do prostej o równaniu \(y = -3x + 5\) jest równy
A.\( -\frac{1}{3} \)
B.\( -3 \)
C.\( \frac{1}{3} \)
D.\( 3 \)
Prostą równoległą do prostej o równaniu \(y=\frac{2}{3}x-\frac{4}{3}\) jest prosta opisana równaniem
A.\( y=-\frac{2}{3}x+\frac{4}{3} \)
B.\( y=\frac{2}{3}x+\frac{4}{3} \)
C.\( y=\frac{3}{2}x-\frac{4}{3} \)
D.\( y=-\frac{3}{2}x-\frac{4}{3} \)
W kartezjańskim układzie współrzędnych \((x, y)\) dane są proste \(k\) oraz \(l\) o równaniach \[k: y=-\frac{1}{2}x-7\] \[l: y=(2m-1)x+13\]
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Proste \(k\) oraz \(l\) są równoległe, gdy A.\( m=-\frac{1}{2} \)
B.\( m=\frac{1}{4} \)
C.\( m=\frac{3}{2} \)
D.\( m=2 \)
Na płaszczyźnie, w kartezjańskim układzie współrzędnych \((x, y)\), dana jest prosta \(k\) o równaniu \(y = −3x + 1\). Jedną z prostych prostopadłych do prostej \(k\) jest prosta o równaniu
Dokończ zdania. Wybierz odpowiedź spośród A–D oraz odpowiedź spośród E–H.
1. Jedną z prostych równoległych do prostej \(k\) jest prosta o równaniu A.\( y = 3x + 2 \)
B.\( y = -3x + 2 \)
C.\( y = \frac{1}{3}x + 1 \)
D.\( y = -\frac{1}{3}x + 1 \)
E.\( y = \frac{1}{3}x + 2 \)
F.\( y = -\frac{1}{3}x + 2 \)
G.\( y = 3x + 1 \)
H.\( y = -3x + 1 \)
Prosta \(l\) ma równanie \(y=-\frac{1}{4}x+7\). Wskaż równanie prostej prostopadłej do prostej \(l\).
A.\( y=\frac{1}{4}x+1 \)
B.\( y=-\frac{1}{4}x-7 \)
C.\( y=4x-1 \)
D.\( y=-4x+7 \)
Prosta o równaniu \(y=\frac{2}{m}x+1\) jest prostopadła do prostej o równaniu \(y=-\frac{3}{2}x-1\). Stąd wynika, że
A.\( m=-3 \)
B.\( m=\frac{2}{3} \)
C.\( m=\frac{3}{2} \)
D.\( m=3 \)
Prostymi równoległymi są wykresy funkcji liniowych:
A.\( y=\frac{4}{3}x+5\ \) i \(\ y=-\frac{3}{4}x+5\)
B.\( y=\frac{4}{3}x+5\ \) i \(\ y=-\frac{4}{3}x+5\)
C.\( y=\frac{4}{3}x+5\ \) i \(\ y=\frac{3}{4}x-5\)
D.\( y=\frac{4}{3}x+5\ \) i \(\ y=\frac{4}{3}x-5\)
Proste \(y=-3x+4\) i \(y=\left ( \frac{1}{3}a^2-\frac{4}{3} \right )x\) są prostopadłe, jeżeli
A.\( a=-2\ \) lub \(\ a=2\)
B.\( a=2 \)
C.\( a=\sqrt{5} \)
D.\( a=-\sqrt{5}\ \) lub \(\ a=\sqrt{5}\)
Prostą przechodzącą przez punkt \(A = (1,1)\) i równoległą do prostej \(y=0{,}5x-1\) opisuje równanie
A.\( y=-2x-1 \)
B.\( y=\frac{1}{2}x+\frac{1}{2} \)
C.\( y=-\frac{1}{2}x+\frac{1}{2} \)
D.\( y=2x-1 \)
Proste \(l\) i \(k\) są prostopadłe i \(l{:}\ 2x-9y+6=0,\ k{:}\ y=ax+b\). Wówczas:
A.\( a=-\frac{2}{9} \)
B.\( a=\frac{2}{9} \)
C.\( a=-\frac{9}{2} \)
D.\( a=\frac{9}{2} \)
Wskaż równanie prostej, która jest równoległa do prostej o równanie \(12x+4y+3=0\)
A.\( y=12x \)
B.\( y=-12x \)
C.\( y=3x \)
D.\( y=-3x \)
Prosta prostopadła do prostej \(l\) o równaniu \(4x-5y+6=0\) ma wzór:
A.\( y=-\frac{1}{5}x+b \)
B.\( y=-\frac{1}{4}x+b \)
C.\( y=-\frac{4}{5}x+b \)
D.\( y=-\frac{5}{4}x+b \)
Wskaż równanie prostej prostopadłej do prostej o równaniu \(2x-4y=5\).
A.\( y=\frac{1}{2}x \)
B.\( y=-\frac{1}{2} \)
C.\( y=2x \)
D.\( y=-2x \)
Dane są równania czterech prostych: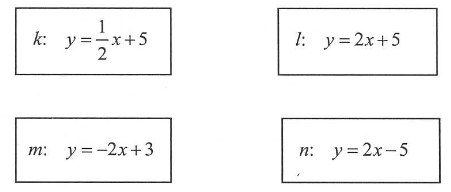 
Prostopadłe są proste:
Prostopadłe są proste: A.\(l\) i \( n \)
B.\(l\) i \( m \)
C.\(k\) i \( n \)
D.\(k\) i \( m \)
Wybierz i zaznacz równanie opisujące prostą prostopadłą do prostej o równaniu \(y=\frac{1}{2}x+1\).
A.\( y=-2x+1 \)
B.\( y=0{,}5x-1 \)
C.\( y=-\frac{1}{2}x+1 \)
D.\( y=2x-1 \)
Wskaż równanie prostej równoległej do prostej o równaniu \( y=2x-7 \).
A.\(y=-2x+7 \)
B.\(y=-\frac{1}{2}x+5 \)
C.\(y=\frac{1}{2}x+2 \)
D.\(y=2x-1 \)
Wskaż równanie prostej równoległej do prostej o równaniu \( 3x-6y+7=0 \)
A.\(y=\frac{1}{2}x \)
B.\(y=-\frac{1}{2}x \)
C.\(y=2x \)
D.\(y=-2x \)
Wyznacz wszystkie parametry \(m\) dla których prosta o równaniu \(y = (m - 1)x + 5\) jest
- rosnąca
- równoległa do prostej \(y = -6x + 3\)
Wyznacz wszystkie parametry \(m\) dla których prosta o równaniu \(y = (3 - 2m)x + 5\) jest
- malejąca
- prostopadła do prostej \(y = 2x-3\)
Proste o równaniach \(y=2x-5\) i \(y=(3-m)x+4\) są równoległe. Wynika stąd, że
A.\( m=1 \)
B.\( m=\frac{5}{2} \)
C.\( m=\frac{7}{2} \)
D.\( m=5 \)
Które z poniższych równań opisuje prostą prostopadłą do prostej o równaniu \( y=4x+5 \).
A.\(y=-4x+3 \)
B.\(y=-\frac{1}{4}x+3 \)
C.\(y=\frac{1}{4}x+3 \)
D.\(y=4x+3 \)
Proste o równaniach \(-3y - mx + 12 = 0\) oraz \(y = 6x - 12\) są prostopadłe dla \(m\) równego:
A.\( \frac{1}{2} \)
B.\( -18 \)
C.\( -\frac{1}{2} \)
D.\( 6 \)
Wykresy funkcji liniowych \( f(x)=\frac{\sqrt{5}}{3}x+6 \) oraz \( g(x)=\frac{5}{3\sqrt{5}}x-\frac{1}{6} \) :
A.są prostopadłe
B.przecinają się, ale nie są prostopadłe
C.pokrywają się
D.są równoległe, ale się nie pokrywają
Prosta \(l\) o równaniu \(y=m^2x+3\) jest równoległa do prostej \(k\) o równaniu \(y=(4m-4)x-3\). Zatem:
A.\( m=2 \)
B.\( m=-2 \)
C.\( m=-2-2\sqrt{2} \)
D.\( m=2+2\sqrt{2} \)
Proste o równaniach: \(y=2mx-m^2-1\) oraz \(y=4m^2x+m^2+1\) są prostopadłe dla
A.\( m=-\frac{1}{2} \)
B.\( m=\frac{1}{2} \)
C.\( m=1 \)
D.\( m=2 \)
Proste o równaniach \(y = (m + 2)x + 3\) oraz \(y = (2m - 1)x - 3\) są równoległe, gdy
A.\( m = 2 \)
B.\( m = 3 \)
C.\( m = 0 \)
D.\( m = 1 \)
Proste o równaniach \(y = (3m - 4)x + 2\) oraz \(y = (12 - m)x + 3m\) są równoległe, gdy
A.\( m = 4 \)
B.\( m = 3 \)
C.\( m = -4 \)
D.\( m = -3 \)
Proste o równaniach \(y = (2m + 2)x - 2019\) oraz \(y = (3m - 3)x + 2019\) są równoległe, gdy
A.\( m = -1 \)
B.\( m = 0 \)
C.\( m = 1 \)
D.\( m = 5 \)
Proste o równaniach \(y=(4m+1)x-19\) oraz \(y=(5m-4)x+20\) są równoległe gdy
A.\( m=5 \)
B.\( m=-\frac{1}{4} \)
C.\( m=\frac{5}{4} \)
D.\( m=-5 \)
Proste o równaniach \(y=3x-5\) oraz \(y=\frac{m-3}{2}x+\frac{9}{2}\) są równoległe, gdy
A.\( m=1 \)
B.\( m=3 \)
C.\( m=6 \)
D.\( m=9 \)
Proste o równaniach \(y=(m-2)x\) oraz \(y=\frac{3}{4}x+7\) są równoległe. Wtedy
A.\( m=-\frac{5}{4} \)
B.\( m=\frac{2}{3} \)
C.\( m=\frac{11}{4} \)
D.\( m=\frac{10}{3} \)
Równania \( y=-\frac{3}{4}x+\frac{5}{4} \text{ oraz } y=-\frac{4}{3} \) opisują dwie proste
A.przecinające się pod kątem o mierze \( 90 ^\circ \).
B.pokrywające się.
C.przecinające się pod kątem różnym od \( 90 ^\circ \).
D.równoległe i różne.
Wyznacz wszystkie parametry \(m\) dla których proste \(y=(m^2+1)x-3\) oraz \(y=-\frac{1}{3}x+2m\) są prostopadłe.
Napisz równanie prostej równoległej do prostej o równaniu \(2x-y-11=0\) i przechodzącej przez punkt \(P=(1,2)\).
Prosta \(l\) jest równoległa do prostej \(y=-\frac{1}{2}x+2\). Na prostej \(l\) leży punkt \(P=(0,7)\). Zatem równanie prostej \(l\) ma postać
A.\( y=2x \)
B.\( y=2x+7 \)
C.\( y=-\frac{1}{2}x \)
D.\( y=-\frac{1}{2}x+7 \)
Funkcja liniowa \(f\) jest określona wzorem \(f(x) = -x + 1\). Funkcja \(g\) jest liniowa. W kartezjańskim układzie współrzędnych \((x, y)\) wykres funkcji \(g\) przechodzi przez punkt \(P = (0, -1)\) i jest prostopadły do wykresu funkcji \(f\).
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Wzorem funkcji \(g\) jest A.\( g(x)=x+1 \)
B.\( g(x)=-x-1 \)
C.\( g(x)=-x+1 \)
D.\( g(x)=x-1 \)
Dany jest trapez \(ABCD\), w którym boki \(AB\) i \(CD\) są równoległe oraz \(C=(3,5)\). Wierzchołki \(A\) i \(B\) tego trapezu leżą na prostej o równaniu \(y=5x+3\). Wtedy bok \(CD\) tego trapezu zawiera się w prostej o równaniu
A.\( y=3x+5 \)
B.\( y=-\frac{1}{5}x+3 \)
C.\( y=5x-10 \)
D.\( y=-\frac{1}{5}x+\frac{28}{5} \)
Na rysunku, w kartezjańskim układzie współrzędnych \((x, y)\), przedstawiono dwie proste równoległe, które są interpretacją geometryczną jednego \(z\) poniższych układów równań A-D.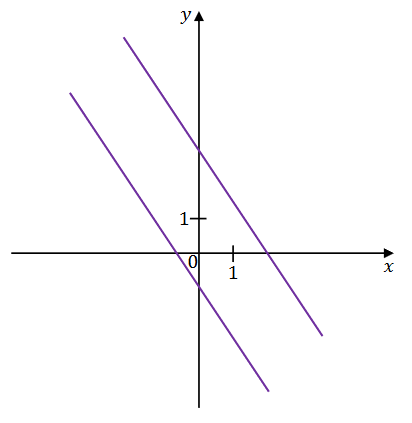 
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Układem równań, którego interpretację geometryczną przedstawiono na rysunku, jest A.\(\left\{\begin{array}{l}y=-\frac{3}{2} x+3 \\ y=-\frac{3}{2} x-1\end{array}\right.\)
B.\(\left\{\begin{array}{l}y=\frac{3}{2} x+3 \\ y=-\frac{2}{3} x-1\end{array}\right.\)
C.\(\left\{\begin{array}{l}y=\frac{3}{2} x+3 \\ y=\frac{3}{2} x-1\end{array}\right.\)
D.\(\left\{\begin{array}{l}y=-\frac{3}{2} x-3 \\ y=\frac{3}{2} x+1\end{array}\right.\)
Na rysunku przedstawione są dwie proste równoległe \(k\) i \(l\) o równaniach \(y=ax+b\) oraz \(y=mx+n\). Początek układu współrzędnych leży między tymi prostymi.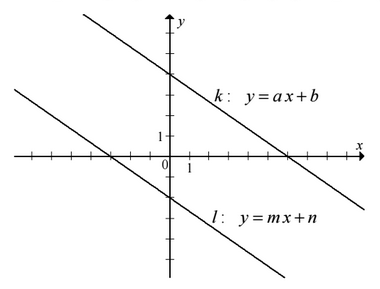 
Zatem
Zatem A.\( a\cdot m\gt 0 \) i \(b\cdot n\gt 0\)
B.\( a\cdot m\gt 0 \) i \(b\cdot n\lt 0\)
C.\( a\cdot m\lt 0 \) i \(b\cdot n\gt 0\)
D.\( a\cdot m\lt 0 \) i \(b\cdot n\lt 0\)
Punkty \(A = (-3, 4)\) i \(C = (1,3)\) są wierzchołkami kwadratu \(ABCD\). Wyznacz równanie prostej zawierającej przekątną \(BD\) tego kwadratu.