Równanie prostej przechodzącej przez dwa punkty
Poziom podstawowy
Jeżeli znamy współrzędne dwóch punktów należących do prostej, to możemy wyznaczyć jej równanie.Najczęściej będziemy wyznaczali równanie prostej zapisane w postaci kierunkowej.
Definicja
Równanie prostej \(y = ax + b\) nazywamy równaniem kierunkowym prostej. Równanie prostej przechodzącej przez punkty \(A = (x_A, y_A)\) i \(B = (x_B, y_B)\) można zapisać wzorem: \[(y-y_A)(x_B-x_A)-(y_B-y_A)(x-x_A)=0\]
W praktyce rzadko korzystamy z tego wzoru. Lepiej sprawdza się metoda opisana w poniższym przykładzie. Wyznacz równanie prostej przechodzącej przez punkty \(A=(5,6)\) oraz \(B=(7,11)\).
Zapisujemy równanie prostej w postaci kierunkowej: \[y=ax+b\] Skoro punkt \(A\) należy do prostej, to możemy podstawić jego współrzędne do równania tej prostej (pod \(x\) współrzędną \(x\)-ową punktu \(A\), a pod \(y\) współrzędną \(y\)-ową punktu \(A\)): \[6=a\cdot 5+b\] Tak samo możemy podstawić do równania współrzędne punktu \(B\): \[11=a\cdot 7+b\] W ten sposób otrzymujemy dwa równania z dwiema niewiadomymi \(a\) oraz \(b\): \begin{cases} 6=5a+b \\ 11=7a+b \end{cases} Rozwiązujemy powyższy układ równań, np. odejmując równania stronami: \[\begin{split} 6-11&=5a-7a\\[6pt] -5&=-2a\\[6pt] a&=\frac{5}{2} \end{split}\] Teraz możemy obliczyć \(b\) np. z pierwszego równania: \[b=6-5a=6-5\cdot \frac{5}{2}=\frac{12}{2}-\frac{25}{2}=-\frac{13}{2}\] Czyli ostatecznie szukane równanie prostej jest postaci: \[y=\frac{5}{2}x-\frac{13}{2}\]
Dane są punkty \(A = (0,2)\) oraz \(B = (2,1)\). Wyznacz równanie prostej \(AB\).
Dane są punkty \(A = (6, 1)\) i \(B = (3, 3)\). Współczynnik kierunkowy prostej \(AB\) jest równy
A.\( -\frac{2}{3} \)
B.\( -\frac{3}{2} \)
C.\( \frac{3}{2} \)
D.\( \frac{2}{3} \)
Do wykresu funkcji liniowej należą punkty \(A=(1,2)\) i \(B=(-2,5)\). Funkcja \(f\) ma wzór
A.\( f(x)=x+3 \)
B.\( f(x)=x-3 \)
C.\( f(x)=-x-3 \)
D.\( f(x)=-x+3 \)
O funkcji liniowej \( f \) wiadomo, że \( f(1)=2 \). Do wykresu tej funkcji należy punkt \( P=(-2,3) \). Wzór funkcji \( f \) to
A.\(f(x)=-\frac{1}{3}x+\frac{7}{3} \)
B.\(f(x)=-\frac{1}{2}x+2 \)
C.\(f(x)=-3x+7 \)
D.\(f(x)=-2x+4 \)
Wskaż równanie prostej, której fragment przedstawiony jest na poniższym wykresie 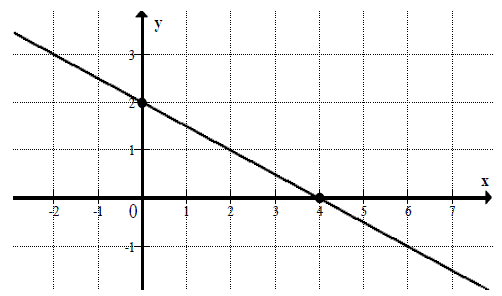
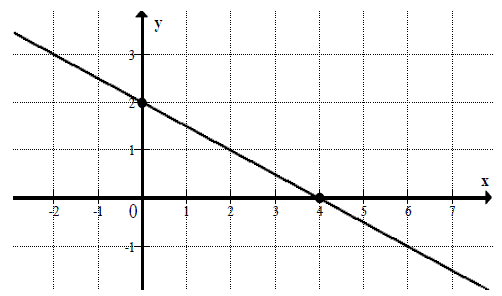
A.\( x-2y-4=0 \)
B.\( x+2y+4=0 \)
C.\( x-2y+4=0 \)
D.\( x+2y-4=0 \)
Dane są punkty \(M=(3,-5)\) oraz \(N=(-1,7)\). Prosta przechodząca przez te punkty ma równanie
A.\( y=-3x+4 \)
B.\( y=3x-4 \)
C.\( y=-\frac{1}{3}x+4 \)
D.\( y=3x+4 \)
Współczynnik kierunkowy prostej, na której leżą punkty \(A = (−4,3)\) oraz \(B = (8,7)\), jest równy
A.\( a=3 \)
B.\( a=-1 \)
C.\( a=\frac{5}{6} \)
D.\( a=\frac{1}{3} \)