Postać iloczynowa funkcji kwadratowej

Poziom podstawowy

Definicja

Postać iloczynowa funkcji kwadratowej to: \[ f(x)=a(x-x_1)(x-x_2) \] gdzie: \(a \ne 0\), \(x_1\) i \(x_2\) są miejscami zerowymi funkcji \(f(x)\).

Uwaga! Jeżeli funkcja kwadratowa nie ma miejsc zerowych, to postać iloczynowa nie istnieje.

Zaletą postaci iloczynowej jest to, że widać z niej od razu miejsca zerowe funkcji kwadratowej.

Współczynnik \(a\) pozwala określić, czy ramiona paraboli są skierowane do góry (gdy \(a > 0\)), czy do dołu (gdy \(a < 0\)).

Wzory na miejsca zerowe

Dla funkcji kwadratowej danej w postaci ogólnej \(f(x)=ax^2+bx+c\), gdzie \(a \ne 0\), mamy:

Jeżeli \(\Delta \gt 0\), to: \[x_1=\frac{-b-\sqrt{\Delta }}{2a}\quad \lor \quad x_2=\frac{-b+\sqrt{\Delta }}{2a}\]
Jeżeli \(\Delta = 0\), to: \[x_1=x_2=\frac{-b}{2a}\]

gdzie: \(\Delta = b^2-4ac\).

Miejscem zerowym funkcji kwadratowej \(y=-(-x-7)(1+x)\) jest

A.\( x=7 \)

B.\( x=1 \)

C.\( x=0 \)

D.\( x=-1 \)

Zbiorem wartości funkcji \(f(x) = -2(x + 3)(x - 4)\) jest przedział:

A.\( \left ( -\infty , 24\frac{1}{2} \right \rangle \)

B.\( \left \langle -24\frac{1}{2},+\infty \right ) \)

C.\( \left \langle 24\frac{1}{2},+\infty \right ) \)

D.\( \left \langle -25\frac{1}{2},+\infty \right ) \)

Na rysunku przedstawiono fragment wykresu funkcji kwadratowej \( f \).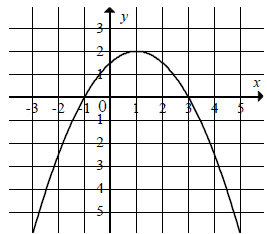

Funkcja \( f \) określona jest wzorem

A.\(f(x)=-\frac{1}{2}(x-3)(x+1) \)

B.\(f(x)=\frac{1}{2}(x-3)(x+1) \)

C.\(f(x)=-\frac{1}{2}(x+3)(x-1) \)

D.\(f(x)=\frac{1}{2}(x+3)(x-1) \)

Wskaż rysunek, na którym przedstawiony jest wykres funkcji kwadratowej, określonej wzorem \( f(x)=(x-2)(x+4) \) .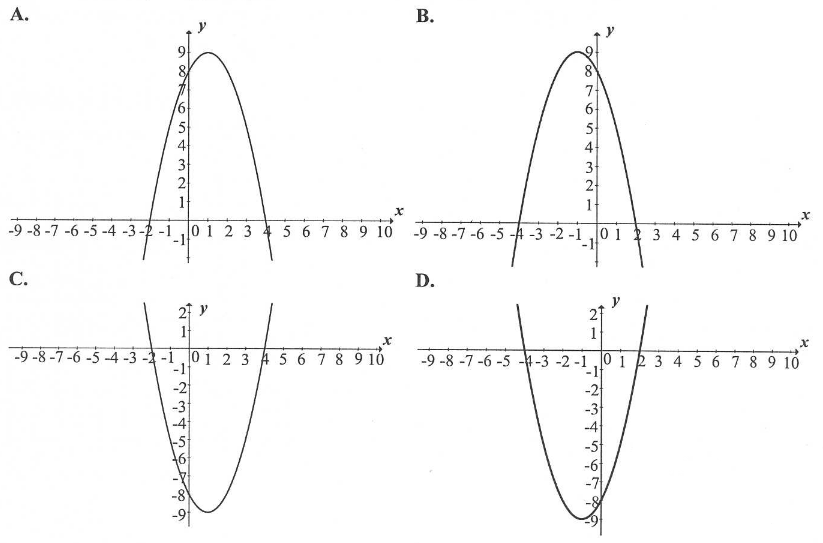

Funkcja kwadratowa \(f(x)=-2(x-5)(x+1)\) jest malejąca w zbiorze

A.\((-1,5)\)

B.\( ( -\infty ,2 \rangle \)

C.\(\langle 2,+\infty )\)

D.\((-\infty ,-1)\cup (5,+\infty )\)

Suma pierwiastków równania \(17(x-1)(2-x)=0\) jest miejscem zerowym funkcji \(f(x)=(m-1)x-6\). Wtedy

A.\( m=0 \)

B.\( m=1 \)

C.\( m=2 \)

D.\( m=3 \)

Liczby \(x_1, x_2\) są rozwiązaniami równania \(4(x + 2)(x - 6) = 0\) . Suma \({x_1}^2 + {x_2}^2\) jest równa

A.\( 16 \)

B.\( 32 \)

C.\( 40 \)

D.\( 48 \)

Liczby \(x_1\) oraz \(x_2\) są rozwiązaniami równania \((x + 1)(2 - x) = 0\). Oblicz \({x_1}^2+x_1x_2+{x_2}^2\).

\(3\)

Pierwiastki \( x_1, x_2 \) równania \( 2(x+2)(x-2)=0 \) spełniają warunek

A.\(\frac{1}{x_1}+\frac{1}{x_2}=\frac{1}{2} \)

B.\(\frac{1}{x_1}+\frac{1}{x_2}=\frac{1}{4} \)

C.\(\frac{1}{x_1}+\frac{1}{x_2}=-1 \)

D.\(\frac{1}{x_1}+\frac{1}{x_2}=0 \)