Matura podstawowa z matematyki - kurs - funkcja kwadratowa

Drukuj

Poziom podstawowy

Szybka nawigacja do zadania numer: 5 10 15 20 25 30 35 40 .

W tej lekcji wideo znajdziesz bardzo dokładne omówienie pojęcia funkcji kwadratowej.

Czas nagrania: 45 min.

Dana jest parabola o równaniu \(y=x^2+8x-14\). Pierwsza współrzędna wierzchołka tej paraboli jest równa

A.\( x=-8 \)

B.\( x=-4 \)

C.\( x=4 \)

D.\( x=8 \)

Wskaż fragment wykresu funkcji kwadratowej, której zbiorem wartości jest \(\langle -2,+\infty )\).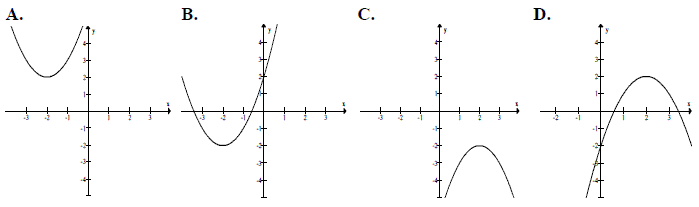

Na jednym z poniższych rysunków przedstawiono fragment wykresu funkcji \(y=x^2+2x-3\). Wskaż ten rysunek.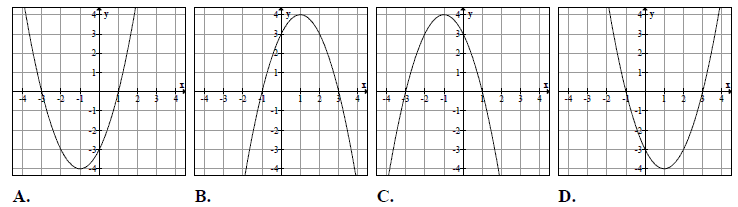

Wierzchołkiem paraboli będącej wykresem funkcji określonej wzorem \(f(x)=x^2-4x+4\) jest punkt o współrzędnych

A.\( (0,2) \)

B.\( (0,-2) \)

C.\( (-2,0) \)

D.\( (2,0) \)

Miejscem zerowym funkcji kwadratowej \(y=-(-x-7)(1+x)\) jest

A.\( x=7 \)

B.\( x=1 \)

C.\( x=0 \)

D.\( x=-1 \)

Wykresem funkcji kwadratowej \(f(x)=-3x^2+3\) jest parabola o wierzchołku w punkcie

A.\( (3,0) \)

B.\( (0,3) \)

C.\( (-3,0) \)

D.\( (0,-3) \)

Miejscami zerowymi funkcji kwadratowej \( y = -3(x-7)(x+2) \) są

A.\(x=7, x=-2 \)

B.\(x=-7, x=-2 \)

C.\(x=7, x=2 \)

D.\(x=-7, x=2 \)

Liczby \(x_1, x_2\) są rozwiązaniami równania \(4(x + 2)(x - 6) = 0\) . Suma \({x_1}^2 + {x_2}^2\) jest równa

A.\( 16 \)

B.\( 32 \)

C.\( 40 \)

D.\( 48 \)

Wskaż funkcję kwadratową, której zbiorem wartości jest przedział \( (-\infty ;3 \rangle \).

A.\(f(x)=-(x-2)^2+3 \)

B.\(f(x)=(2-x)^2+3 \)

C.\(f(x)=-(x+2)^2-3 \)

D.\(f(x)=(2-x)^2-3 \)

Wykres funkcji kwadratowej \( f(x)=3(x+1)^2-4 \) nie ma punktów wspólnych z prostą o równaniu

A.\(y=1 \)

B.\(y=-1 \)

C.\(y=-3 \)

D.\(y=-5 \)

Prosta o równaniu \( y=a \) ma dokładnie jeden punkt wspólny z wykresem funkcji kwadratowej \( f(x)=-x^2+6x-10 \). Wynika stąd, że

A.\(a=3 \)

B.\(a=0 \)

C.\(a=-1 \)

D.\(a=-3 \)

Jaka jest najmniejsza wartość funkcji kwadratowej \( f(x)=x^2+4x-3 \) w przedziale \( \langle 0, 3 \rangle \)?

A.\(-7 \)

B.\(-4 \)

C.\(-3 \)

D.\(-2 \)

Oblicz największą wartość funkcji \(f(x)=-2x^2+16x-15\) w przedziale \(\langle -2,3 \rangle\).

\(15\)

Oblicz najmniejszą wartość funkcji kwadratowej \(f(x)=x^2-6x+1\) w przedziale \(\langle 0,1 \rangle\).

\(-4\)

Funkcja kwadratowa \(f(x)=-2(x-5)(x+1)\) jest malejąca w zbiorze

A.\((-1,5)\)

B.\( ( -\infty ,2 \rangle \)

C.\(\langle 2,+\infty )\)

D.\((-\infty ,-1)\cup (5,+\infty )\)

Wierzchołkiem paraboli o równaniu \(y=-3(x-2)^2+4\) jest punkt o współrzędnych

A.\( (-2, -4) \)

B.\( (-2, 4) \)

C.\( (2, -4) \)

D.\( (2, 4) \)

Wierzchołek paraboli o równaniu \(y=(x+1)^2+2c\) leży na prostej o równaniu \(y=6\). Wtedy

A.\( c=-6 \)

B.\( c=-3 \)

C.\( c=3 \)

D.\( c=6 \)

Na wykresie przedstawiony jest trójmian \(y = ax^2 + bx + c\).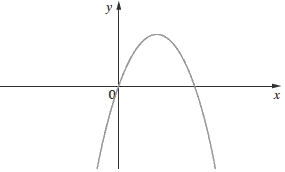

Wynika z tego, że:

A.\( b\lt 0 \)

B.\( b>0 \)

C.\( b\le 0 \)

D.\( b\ge 0 \)

Wierzchołek paraboli, która jest wykresem funkcji \( y=x^2 -2x-3 \) leży na prostej:

A.\(y=-4 \)

B.\(y=4 \)

C.\(y=1 \)

D.\(y=2 \)

Rysunek obok przedstawia wykres funkcji kwadratowej \( f \). Zapisz wzór funkcji \( f \) w postaci ogólnej i podaj jej zbiór wartości.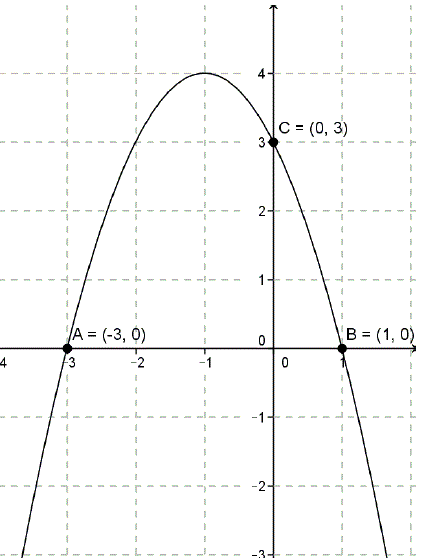

\(f(x)=-x^2-2x+3\)
\(ZW=(-\infty ;4\rangle \)

Na rysunku przedstawiono fragment wykresu funkcji kwadratowej \( f \).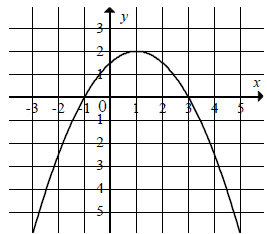

Funkcja \( f \) określona jest wzorem

A.\(f(x)=-\frac{1}{2}(x-3)(x+1) \)

B.\(f(x)=\frac{1}{2}(x-3)(x+1) \)

C.\(f(x)=-\frac{1}{2}(x+3)(x-1) \)

D.\(f(x)=\frac{1}{2}(x+3)(x-1) \)

Wykresem funkcji kwadratowej \( f(x)=2x^2+bx+c \) jest parabola, której wierzchołkiem jest punkt \( W=(4,0) \). Oblicz wartości współczynników \( b \) i \( c \).

\(b=-16\), \(c=32\)

Wskaż rysunek, na którym przedstawiony jest wykres funkcji kwadratowej, określonej wzorem \( f(x)=(x-2)(x+4) \) .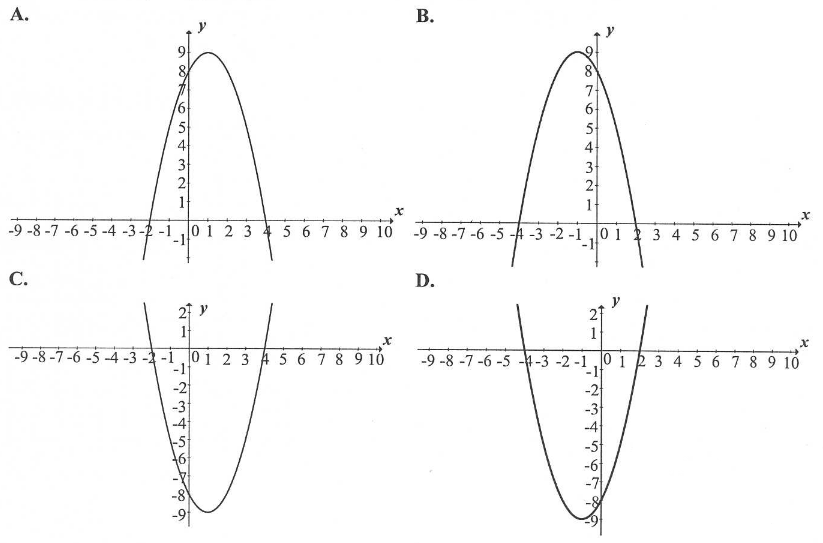

Funkcja kwadratowa, której zbiorem wartości jest przedział \( ( -\infty, -3\rangle \) , może być określona wzorem

A.\(y=(x+2)^2-3 \)

B.\(y=-(x+3)^2 \)

C.\(y=-(x-2)^2-3 \)

D.\(y=-x^2+3 \)

Wskaż równanie osi symetrii paraboli określonej równaniem \( y=-x^2+4x-11 \).

A.\(x=-4 \)

B.\(x=-2 \)

C.\(x=2 \)

D.\(x=4 \)

Funkcja kwadratowa \(y=x^2+bx+c\) jest malejąca dla \(x\in (-\infty ;2 \rangle\) a zbiorem jej wartości jest przedział \(\langle -4;\infty )\). Postać kanoniczna tej funkcji opisana jest wzorem

A.\( f(x)=(x-2)^2-4 \)

B.\( f(x)=(x+2)^2+4 \)

C.\( f(x)=(x+4)^2+2 \)

D.\( f(x)=(x-4)^2+2 \)

Dwie funkcje \(f(x)=2x-1\) oraz \(g(x)=-x^2\) określone są w zbiorze \(\mathbb{R}.\) Wówczas wykres funkcji \(h\) określonej wzorem \(h(x)=f(x)+g(x)\) jest przedstawiony na rysunku: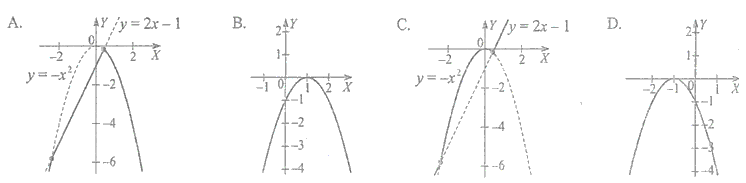

Liczby \(x_1, x_2\) są różnymi rozwiązaniami równania \(x^2-7=0\). Wtedy wyrażenie \(|x_1-x_2|\) jest równe

A.\( 0 \)

B.\( \sqrt{7} \)

C.\( -\sqrt{7} \)

D.\( 2\sqrt{7} \)

Wykres funkcji \(f(x)=x^2-2x-8,\) gdzie \(x \in \mathbb{R}\), przecina oś \(OX\) w punktach \(A\) i \(B\).

Wyznacz współrzędne punktów \(A\) i \(B\).
Oblicz pole trójkąta \(AWB\), jeśli \(W\) jest wierzchołkiem paraboli będącej wykresem funkcji \(f\).

\(A=(-2,0)\), \(B=(4,0)\), \(P_{\Delta AWB}=27\)

Wykaż, że jeżeli \(c\lt 0\), to trójmian kwadratowy \(y=x^2+bx+c\) ma dwa różne miejsca zerowe.

Liczby \(x_1\) oraz \(x_2\) są rozwiązaniami równania \(x^2 - 9 = 0\). Oblicz wartość liczbową wyrażenia \(\frac{x_1+x_2}{2}\).

\(0\)

\( x_1 \) jest mniejszym, zaś \( x_2 \)większym miejscem zerowym funkcji \( f(x)=2x^2+10x+12 \). Wyrażenie \( x_2-x_1 \) ma wartość:

A.\(-1 \)

B.\(1 \)

C.\(-2 \)

D.\(2 \)

Zbiorem wartości funkcji \(f(x) = -2(x + 3)(x - 4)\) jest przedział:

A.\( \left ( -\infty , 24\frac{1}{2} \right \rangle \)

B.\( \left \langle -24\frac{1}{2},+\infty \right ) \)

C.\( \left \langle 24\frac{1}{2},+\infty \right ) \)

D.\( \left \langle -25\frac{1}{2},+\infty \right ) \)

Liczby \(x_1\) oraz \(x_2\) są rozwiązaniami równania \((x + 1)(2 - x) = 0\). Oblicz \({x_1}^2+x_1x_2+{x_2}^2\).

\(3\)

W dwóch hotelach wybudowano prostokątne baseny. Basen w pierwszym hotelu ma powierzchnię \(240\) m². Basen w drugim hotelu ma powierzchnię \(350\) m² oraz jest o \(5\) m dłuższy i \(2\) m szerszy niż w pierwszym hotelu. Oblicz, jakie wymiary mogą mieć baseny w obu hotelach. Podaj wszystkie możliwe odpowiedzi.

\(8\times 30\) i \(10\times 35\) lub \(12\times 20\) i \(14\times 25\)

Kolarz pokonał trasę \(114\) km. Gdyby jechał ze średnią prędkością mniejszą o \(9{,}5\) km/h, to pokonałby tę trasę w czasie o \(2\) godziny dłuższym. Oblicz, z jaką średnią prędkością jechał ten kolarz.

\(v=28{,}5\) km/h

Miasto \(A\) i miasto \(B\) łączy linia kolejowa długości \(210\) km. Średnia prędkość pociągu pospiesznego na tej trasie jest o \(24\) km/h większa od średniej prędkości pociągu osobowego. Pociąg pospieszny pokonuje tę trasę o \(1\) godzinę krócej niż pociąg osobowy. Oblicz czas pokonania tej drogi przez pociąg pospieszny.

\(t=2{,}5\) h

Adam rozwiązywał codziennie taką sama liczbę zadań i w sumie rozwiązał \(60\) zadań. Jeśli rozwiązywałby codziennie o \(6\) zadań więcej, to rozwiązałby te zadania o \(5\) dni krócej. Oblicz, przez ile dni Adam rozwiązywał zadania przed maturą i ile zadań rozwiązywał każdego dnia.

Przez \(10\) dni rozwiązywał po \(6\) zadań.

W czasie wakacji Marcin przejechał rowerem ze stałą prędkością odległość z miasteczka \(A\) do \(B\) liczącą \(120\) km. Gdyby jechał ze średnią prędkością o \(5\) km/godz. większą, to przejechałby tę odległość w czasie o \(2\) godziny krótszym. Wyznacz średnią rzeczywistą prędkość Marcina i rzeczywisty czas przejazdu.

\(v=15\) km/h, \(t=8\) h

Z dwóch miast \(A\) i \(B\), odległych od siebie o \(18\) kilometrów, wyruszyli naprzeciw siebie dwaj turyści. Pierwszy turysta wyszedł z miasta \(A\) o jedną godzinę wcześniej niż drugi z miasta \(B\). Oblicz prędkość, z jaką szedł każdy turysta, jeżeli wiadomo, że po spotkaniu pierwszy turysta szedł do miasta \(B\) jeszcze \(1{,}5\) godziny, drugi zaś szedł jeszcze \(4\) godziny do miasta \(A\).

\(v_1=4\) km/h, \(v_2=3\) km/h