Matura podstawowa z matematyki - kurs - funkcja liniowa
Poziom podstawowy
Na filmie pokazuję praktyczną metodę na szybkie rysowanie dokładnych wykresów funkcji liniowych.
Czas lekcji: 13 min.
Na rysunku przedstawiony jest fragment wykresu pewnej funkcji liniowej \(y=ax+b\).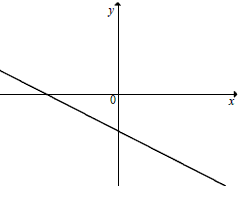 
Jakie znaki mają współczynniki \(a\) i \(b\)?
Jakie znaki mają współczynniki \(a\) i \(b\)? A.\(a\lt 0\) i \(b\lt 0\)
B.\(a\lt 0\) i \(b>0\)
C.\(a>0\) i \(b\lt 0\)
D.\(a>0\) i \(b>0\)
Jeden z rysunków przedstawia wykres funkcji liniowej \(f(x)=ax+b\), gdzie \(a>0\) i \(b\lt 0\). Wskaż ten wykres.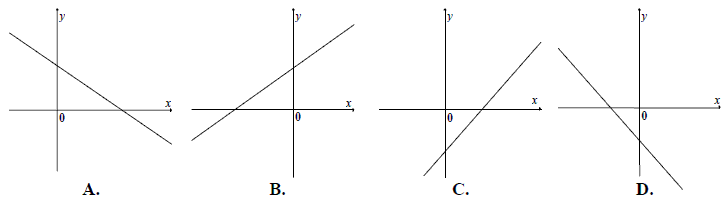 
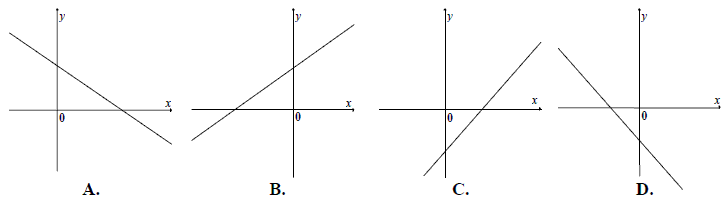
Funkcja \(f(x) = 0{,}5x - 6\)
A.jest malejąca i jej wykres przechodzi przez punkt \((0, 6)\)
B.jest rosnąca i jej wykres przechodzi przez punkt \((0, 6)\)
C.jest malejąca i jej wykres przechodzi przez punkt \((0, -6)\)
D.jest rosnąca i jej wykres przechodzi przez punkt \((0, -6)\)
Funkcja liniowa \( f(x)=(m^2-4)x+2 \) jest malejąca, gdy
A.\(m\in (-\infty,-2) \)
B.\(m\in (2,+\infty) \)
C.\(m\in \lbrace -2,2 \rbrace \)
D.\(m\in (-2,2) \)
Funkcja liniowa \( f(x)=ax+b\ \) jest rosnąca i ma dodatnie miejsce zerowe. Stąd wynika, że
A.\(a>0\) i \( b>0 \)
B.\(a\lt 0\) i \( b\lt 0 \)
C.\(a\lt 0\) i \( b>0 \)
D.\(a>0\) i \( b\lt 0 \)
Dane są punkty \(A = (0,2)\) oraz \(B = (2,1)\). Wyznacz równanie prostej \(AB\).
Dane są punkty \(A = (6, 1)\) i \(B = (3, 3)\). Współczynnik kierunkowy prostej \(AB\) jest równy
A.\( -\frac{2}{3} \)
B.\( -\frac{3}{2} \)
C.\( \frac{3}{2} \)
D.\( \frac{2}{3} \)
Do wykresu funkcji liniowej należą punkty \(A=(1,2)\) i \(B=(-2,5)\). Funkcja \(f\) ma wzór
A.\( f(x)=x+3 \)
B.\( f(x)=x-3 \)
C.\( f(x)=-x-3 \)
D.\( f(x)=-x+3 \)
O funkcji liniowej \( f \) wiadomo, że \( f(1)=2 \). Do wykresu tej funkcji należy punkt \( P=(-2,3) \). Wzór funkcji \( f \) to
A.\(f(x)=-\frac{1}{3}x+\frac{7}{3} \)
B.\(f(x)=-\frac{1}{2}x+2 \)
C.\(f(x)=-3x+7 \)
D.\(f(x)=-2x+4 \)
Prosta o równaniu \(y=\frac{2}{m}x+1\) jest prostopadła do prostej o równaniu \(y=-\frac{3}{2}x-1\). Stąd wynika, że
A.\( m=-3 \)
B.\( m=\frac{2}{3} \)
C.\( m=\frac{3}{2} \)
D.\( m=3 \)
Prosta \(l\) ma równanie \(y=-\frac{1}{4}x+7\). Wskaż równanie prostej prostopadłej do prostej \(l\).
A.\( y=\frac{1}{4}x+1 \)
B.\( y=-\frac{1}{4}x-7 \)
C.\( y=4x-1 \)
D.\( y=-4x+7 \)
Prostymi równoległymi są wykresy funkcji liniowych:
A.\( y=\frac{4}{3}x+5\ \) i \(\ y=-\frac{3}{4}x+5\)
B.\( y=\frac{4}{3}x+5\ \) i \(\ y=-\frac{4}{3}x+5\)
C.\( y=\frac{4}{3}x+5\ \) i \(\ y=\frac{3}{4}x-5\)
D.\( y=\frac{4}{3}x+5\ \) i \(\ y=\frac{4}{3}x-5\)
Proste \(y=-3x+4\) i \(y=\left ( \frac{1}{3}a^2-\frac{4}{3} \right )x\) są prostopadłe, jeżeli
A.\( a=-2\ \) lub \(\ a=2\)
B.\( a=2 \)
C.\( a=\sqrt{5} \)
D.\( a=-\sqrt{5}\ \) lub \(\ a=\sqrt{5}\)
Prostą przechodzącą przez punkt \(A = (1,1)\) i równoległą do prostej \(y=0{,}5x-1\) opisuje równanie
A.\( y=-2x-1 \)
B.\( y=\frac{1}{2}x+\frac{1}{2} \)
C.\( y=-\frac{1}{2}x+\frac{1}{2} \)
D.\( y=2x-1 \)
Proste \(l\) i \(k\) są prostopadłe i \(l{:}\ 2x-9y+6=0,\ k{:}\ y=ax+b\). Wówczas:
A.\( a=-\frac{2}{9} \)
B.\( a=\frac{2}{9} \)
C.\( a=-\frac{9}{2} \)
D.\( a=\frac{9}{2} \)
Prosta prostopadła do prostej \(l\) o równaniu \(4x-5y+6=0\) ma wzór:
A.\( y=-\frac{1}{5}x+b \)
B.\( y=-\frac{1}{4}x+b \)
C.\( y=-\frac{4}{5}x+b \)
D.\( y=-\frac{5}{4}x+b \)
Wskaż równanie prostej prostopadłej do prostej o równaniu \(2x-4y=5\).
A.\( y=\frac{1}{2}x \)
B.\( y=-\frac{1}{2} \)
C.\( y=2x \)
D.\( y=-2x \)
Współczynnik kierunkowy prostej równoległej do prostej o równaniu \(y = -3x + 5\) jest równy
A.\( -\frac{1}{3} \)
B.\( -3 \)
C.\( \frac{1}{3} \)
D.\( 3 \)
Wskaż równanie prostej równoległej do prostej o równaniu \( 3x-6y+7=0 \)
A.\(y=\frac{1}{2}x \)
B.\(y=-\frac{1}{2}x \)
C.\(y=2x \)
D.\(y=-2x \)
Wyznacz wszystkie parametry \(m\) dla których prosta o równaniu \(y = (m - 1)x + 5\) jest
- rosnąca
- równoległa do prostej \(y = -6x + 3\)
Wyznacz wszystkie parametry \(m\) dla których prosta o równaniu \(y = (3 - 2m)x + 5\) jest
- malejąca
- prostopadła do prostej \(y = 2x-3\)
Proste o równaniach \(y=2x-5\) i \(y=(3-m)x+4\) są równoległe. Wynika stąd, że
A.\( m=1 \)
B.\( m=\frac{5}{2} \)
C.\( m=\frac{7}{2} \)
D.\( m=5 \)
Wskaż równanie prostej równoległej do prostej o równaniu \( y=2x-7 \).
A.\(y=-2x+7 \)
B.\(y=-\frac{1}{2}x+5 \)
C.\(y=\frac{1}{2}x+2 \)
D.\(y=2x-1 \)
Które z poniższych równań opisuje prostą prostopadłą do prostej o równaniu \( y=4x+5 \).
A.\(y=-4x+3 \)
B.\(y=-\frac{1}{4}x+3 \)
C.\(y=\frac{1}{4}x+3 \)
D.\(y=4x+3 \)
Napisz równanie prostej równoległej do prostej o równaniu \(2x-y-11=0\) i przechodzącej przez punkt \(P=(1,2)\).
Wybierz i zaznacz równanie opisujące prostą prostopadłą do prostej o równaniu \(y=\frac{1}{2}x+1\).
A.\( y=-2x+1 \)
B.\( y=0{,}5x-1 \)
C.\( y=-\frac{1}{2}x+1 \)
D.\( y=2x-1 \)
Prostą równoległą do prostej o równaniu \(y=\frac{2}{3}x-\frac{4}{3}\) jest prosta opisana równaniem
A.\( y=-\frac{2}{3}x+\frac{4}{3} \)
B.\( y=\frac{2}{3}x+\frac{4}{3} \)
C.\( y=\frac{3}{2}x-\frac{4}{3} \)
D.\( y=-\frac{3}{2}x-\frac{4}{3} \)
Proste o równaniach \(-3y - mx + 12 = 0\) oraz \(y = 6x - 12\) są prostopadłe dla \(m\) równego:
A.\( \frac{1}{2} \)
B.\( -18 \)
C.\( -\frac{1}{2} \)
D.\( 6 \)
Wykresy funkcji liniowych \( f(x)=\frac{\sqrt{5}}{3}x+6 \) oraz \( g(x)=\frac{5}{3\sqrt{5}}x-\frac{1}{6} \) :
A.są prostopadłe
B.przecinają się, ale nie są prostopadłe
C.pokrywają się
D.są równoległe, ale się nie pokrywają
Dane są równania czterech prostych: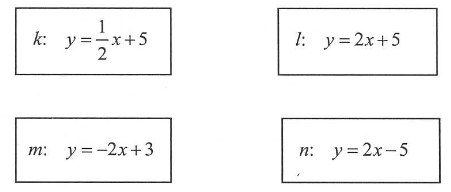 
Prostopadłe są proste:
Prostopadłe są proste: A.\(l\) i \( n \)
B.\(l\) i \( m \)
C.\(k\) i \( n \)
D.\(k\) i \( m \)
Wskaż równanie prostej przechodzącej przez początek układu współrzędnych i prostopadłej do prostej o równaniu \(y=-\frac{1}{3}x+2\).
A.\( y=3x \)
B.\( y=-3x \)
C.\( y=3x+2 \)
D.\( y=\frac{1}{3}x+2 \)
Prosta \(l\) ma równanie \(y = -7x + 2\). Równanie prostej prostopadłej do \(l\) i przechodzącej przez punkt \(P = (0, 1)\) ma postać
A.\( y=7x-1 \)
B.\( y=7x+1 \)
C.\( y=\frac{1}{7}x+1 \)
D.\( y=\frac{1}{7}x-1 \)
Punkt \(A=(0,5)\) leży na prostej \(k\) prostopadłej do prostej o równaniu \(y = x + 1\). Prosta \(k\) ma równanie
A.\( y=x+5 \)
B.\( y=-x+5 \)
C.\( y=x-5 \)
D.\( y=-x-5 \)
Napisz równanie prostej równoległej do prostej o równaniu \(-3x+y-4=0\) i przechodzącej przez punkt \(P=(-1,-4)\).
Prostą prostopadłą do prostej \( y=\frac{1}{2}x-1 \) i przechodzącą przez punkt \( A=(1,1) \) opisuje równanie
A.\(y=2x-1 \)
B.\(y=\frac{1}{2}x+\frac{1}{2} \)
C.\(y=-\frac{1}{2}x+\frac{1}{2} \)
D.\(y=-2x+3 \)