Matura podstawowa 2025 - maj
Poziom podstawowy
Pliki do pobrania: Arkusz można też wydrukować w prawym górnym rogu strony według własnych preferencji.
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Liczba \(\bigl(\sqrt{32}-\sqrt{2}\bigr)^{2}\) jest równa A.\(16\)
B.\(18\)
C.\(30\)
D.\(34\)
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Liczba \(\frac{5^{12}+5^{13}+5^{14}}{5^{12}}\) jest równa A.\(30\)
B.\(31\)
C.\(512\)
D.\(527\)
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Liczba \(\log_{3}108-2\log_{3}2\) jest równa A.\(3\)
B.\(9\)
C.\(\log_{3}104\)
D.\(2\log_{3}54\)
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Dla każdej liczby rzeczywistej \(x\) wartość wyrażenia \(\bigl(3x+2\bigr)^{2}-\bigl(2x-3\bigr)^{2}\) jest równa wartości wyrażenia A.\(5x^{2}-5\)
B.\(5x^{2}+13\)
C.\(5x^{2}+24x-5\)
D.\(5x^{2}+24x-13\)
Wykaż, że dla każdej nieparzystej liczby naturalnej \(n\) liczba \(3n^{2}+2n+7\) jest podzielna przez \(4\).
Dana jest nierówność \[ 3-2(1-2 x) \geq 2 x-17 \] 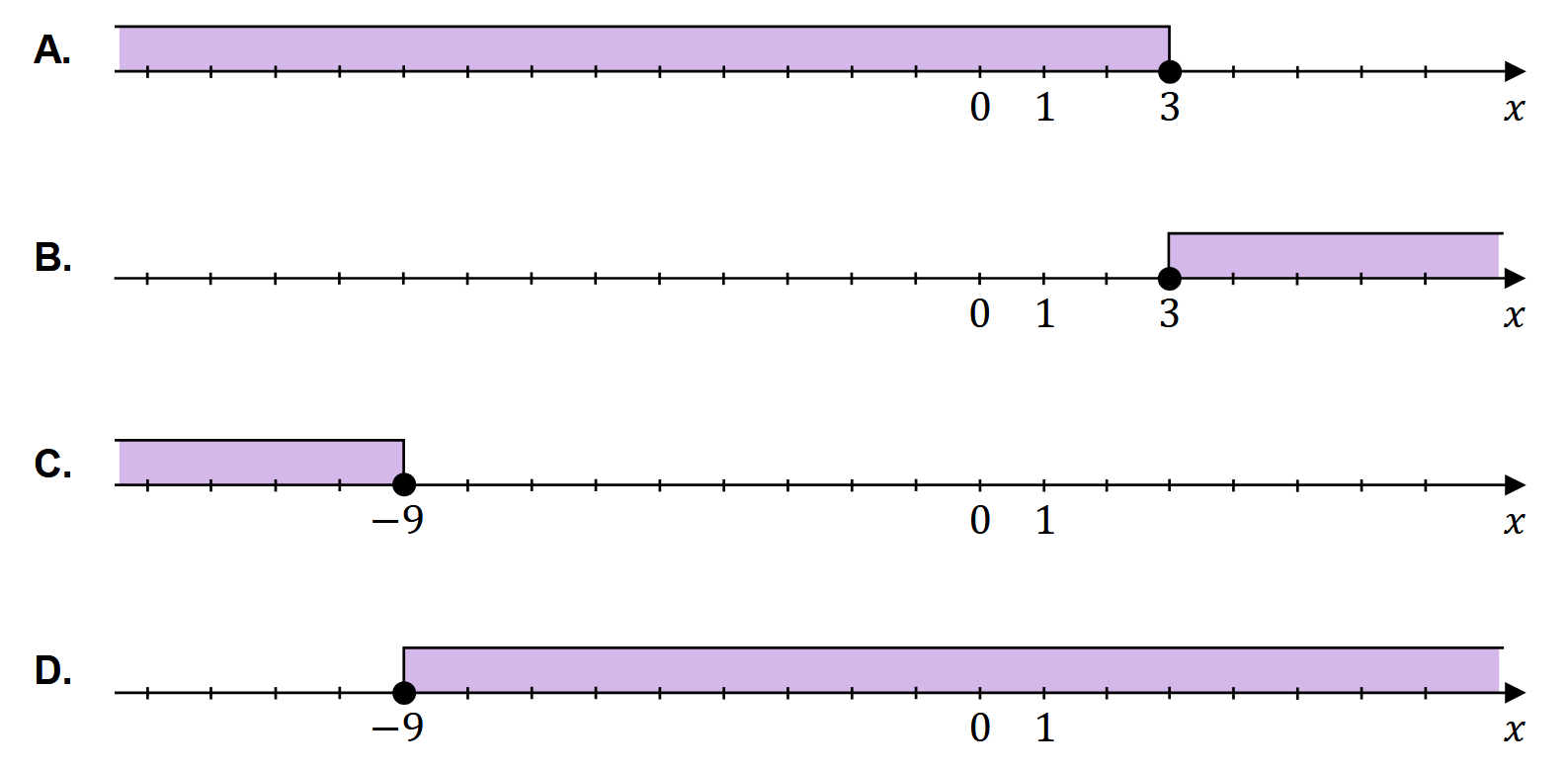
Na którym rysunku poprawnie zaznaczono na osi liczbowej zbiór wszystkich liczb rzeczywistych spełniających powyższą nierówność? Wybierz właściwą odpowiedź spośród podanych.

Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Równanie \(2x(x+3)\left(x^{2}+25\right)=0\) w zbiorze liczb rzeczywistych ma dokładnie A. dwa rozwiązania: \((-3)\) oraz \(0\)
B. dwa rozwiązania: \((-3)\) oraz \(2\)
C. trzy rozwiązania: \((-5),(-3)\) oraz \(0\)
D. cztery rozwiązania: \((-5),(-3), 0\) oraz \(5\)
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Dla każdej liczby rzeczywistej \(x\) różnej od \((-2)\) oraz różnej od \(0\) wartość wyrażenia \(\frac{x^{2}+x}{x^{2}+4x+4}\cdot\frac{x+2}{x}\) jest równa wartości wyrażenia A.\(\frac{x+2}{4x+4}\)
B.\(\frac{x+1}{4x+5}\)
C.\(\frac{x+1}{x+2}\)
D.\(\frac{2x}{x+2}\)
Zarząd firmy wydzielił z budżetu kwotę \(1200000\) złotych łącznie na projekty badawcze dla dwóch zespołów: A i B. W pierwszym półroczu realizacji tych projektów oba zespoły wykorzystały łącznie \(146700\) złotych - zespół A wykorzystał \(13\%\) przyznanych mu środków, a zespół B wykorzystał \(11\%\) przyznanych mu środków.
Oblicz kwotę przyznaną zespołowi A na realizację projektu badawczego. Zapisz obliczenia.
Rozwiąż nierówność \[ 3\left(2 x^{2}+1\right)\lt 11 x \] Zapisz obliczenia.
Funkcja \(f\) jest określona następująco: \[ f(x)= \begin{cases} x+5 & \text{dla } x\in[-4,-2]\\ 3 & \text{dla } x\in(-2,2]\\ -3x+9 & \text{dla } x\in(2,4) \end{cases} \] Wykres funkcji \(y=f(x)\) przedstawiono w kartezjańskim układzie współrzędnych \((x, y)\) na rysunku poniżej. 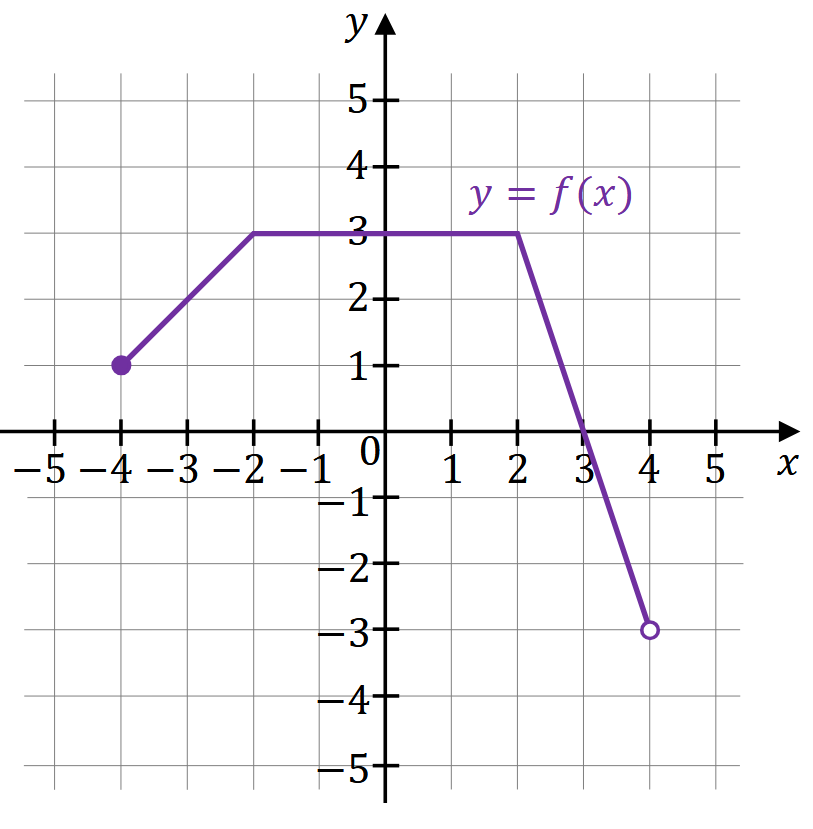

Uzupełnij zdania. Wpisz odpowiednie przedziały w wykropkowanych miejscach, aby zdania były prawdziwe.
- Dziedziną funkcji \(f\) jest przedział …………………… .
- Zbiorem wartości funkcji \(f\) jest przedział …………………… .
- Zbiorem wszystkich argumentów, dla których funkcja \(f\) przyjmuje wartości dodatnie, jest przedział …………………… .
- Zbiorem wszystkich rozwiązań równania \(f(x)=3\) jest przedział …………………… .
W kartezjańskim układzie współrzędnych \((x, y)\) przedstawiono fragment paraboli, która jest wykresem funkcji kwadratowej \(f\) (zobacz rysunek). Wierzchołek tej paraboli ma współrzędne \((3,6)\). Ta parabola przecina oś \(Oy\) w punkcie o współrzędnych \((0,3)\). 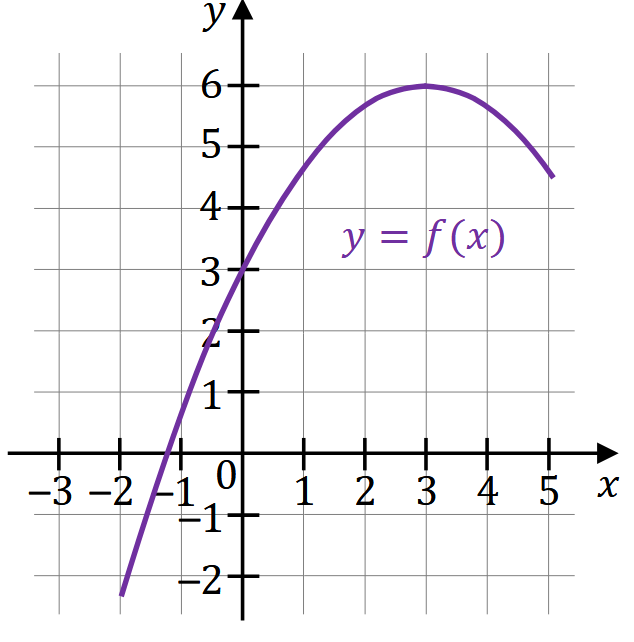

Wyznacz wzór funkcji \(f\) w postaci kanonicznej. Zapisz obliczenia.
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Osią symetrii wykresu funkcji \(f\) jest prosta o równaniu A.\(x = 3\)
B.\(x = -3\)
C.\(y = 6\)
D.\(y = -6\)
Funkcja \(g\) jest określona dla każdej liczby rzeczywistej \(x\) wzorem \(g(x)=f(x)-3\). Liczby \(x_{1}\) oraz \(x_{2}\) są różnymi miejscami zerowymi funkcji \(g\).
Uzupełnij zdanie. Wpisz odpowiednią liczbę w wykropkowanym miejscu, aby zdanie było prawdziwe.
Suma \(x_{1}+x_{2}\) jest równa …………… .Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Funkcja liniowa \(f\) jest określona wzorem \(f(x)=(3-m)\,x-4\). Funkcja \(f\) nie ma miejsca zerowego dla \(m\) równego A.\((-3)\)
B.\(0\)
C.\(3\)
D.\(4\)
Ciąg \(\left(a_{n}\right)\) jest określony następująco: \[ \left\{\begin{array}{l} a_{1}=2 \\ a_{n+1}=2 a_{n}+1 \end{array} \right. \] dla każdej liczby naturalnej \(n \geq 1\).
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Trzeci wyraz ciągu \((a_{n})\) jest równy A.\(4\)
B.\(5\)
C.\(7\)
D.\(11\)
Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, albo F – jeśli jest fałszywe.
| Ciąg \((a_{n})\) jest arytmetyczny. | P | F |
| Ciąg \((a_{n})\) jest geometryczny. | P | F |
Wyznacz wartość \(m\), dla której trzywyrazowy ciąg \[ \left(2 m+11, m^{2}+3,5-m\right) \] jest arytmetyczny i malejący. Zapisz obliczenia.
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Dany jest ciąg geometryczny \((a_{n})\) określony dla każdej liczby naturalnej \(n \ge 1\), w którym \(a_{1}=27\) oraz \(a_{2}=9\). Czwarty wyraz ciągu \((a_{n})\) jest równy A.\(\frac{1}{3}\)
B.\(1\)
C.\(3\)
D.\(729\)
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Kąt \(\alpha\) jest ostry i spełnia warunek \(\sqrt{3}\,\mathrm{tg}\,\alpha = 2\sin\alpha\). Cosinus kąta \(\alpha\) jest równy A.\(\dfrac{1}{2}\)
B.\(\dfrac{\sqrt{2}}{2}\)
C.\(\dfrac{\sqrt{3}}{2}\)
D.\(\dfrac{\sqrt{3}}{3}\)
Dany jest trójkąt prostokątny \(A B C\), w którym bok \(B C\) jest przeciwprostokątną, przyprostokątna \(A B\) ma długość \(6\), a środkowa \(C D\) ma długość \(5\). Oznaczmy kąt \(A D C\) przez \(\alpha\), natomiast kąt \(A B C\) przez \(\beta\) (zobacz rysunek). 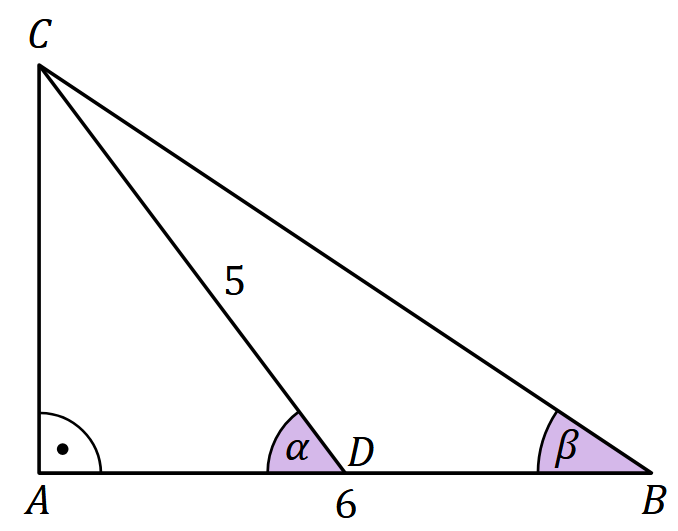

Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Tangens kąta \(\alpha\) jest równy A.\(\dfrac{2}{3}\)
B.\(\dfrac{3}{4}\)
C.\(\dfrac{4}{5}\)
D.\(\dfrac{4}{3}\)
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Sinus kąta \(\beta\) jest równy A.\(\frac{2}{\sqrt{13}}\)
B.\(\frac{3}{\sqrt{13}}\)
C.\(\frac{5}{2\sqrt{13}}\)
D.\(\frac{4}{5}\)
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Punkty \(A\), \(B\) oraz \(C\) leżą na okręgu o środku w punkcie \(O\). Miara kąta \( \sphericalangle BCA \) jest równa \(50^{\circ}\) (zobacz rysunek). 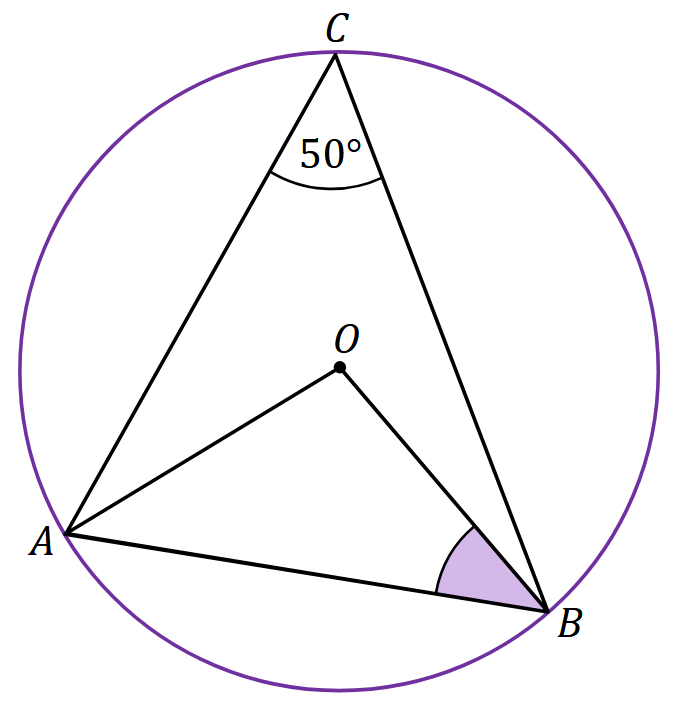 Miara kąta ostrego \( \sphericalangle ABO \) jest równa
Miara kąta ostrego \( \sphericalangle ABO \) jest równa A.\(20^{\circ}\)
B.\(35^{\circ}\)
C.\(40^{\circ}\)
D.\(50^{\circ}\)
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
W trójkącie równoramiennym \(ABC\) dane są: \(|AC| = |BC| = 4\) oraz \(|AB| = 3\). Na boku \(BC\), między punktami \(B\) i \(C\), wybrano taki punkt \(D\), że trójkąty \(ABC\) i \(BDA\) są podobne (zobacz rysunek). 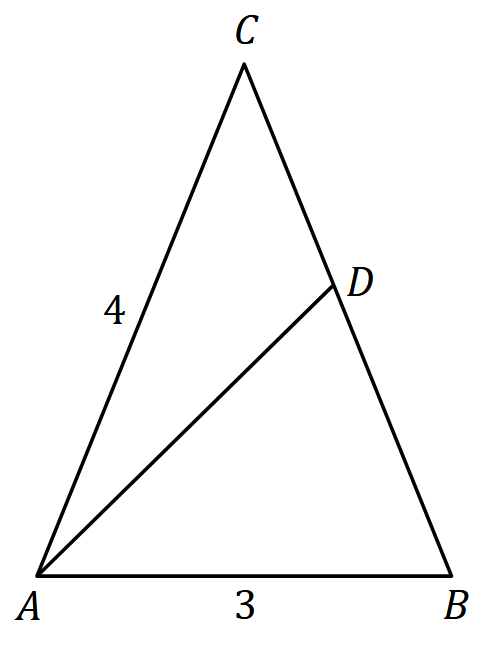 Odcinek \(BD\) ma długość
Odcinek \(BD\) ma długość A.\(2\)
B.\(2{,}25\)
C.\(2{,}5\)
D.\(3\)
Dany jest trójkąt \(ABC\), w którym \(|AB|=11,|BC|=12\) oraz \(|\sphericalangle ABC|=60^{\circ}\) (zobacz rysunek). 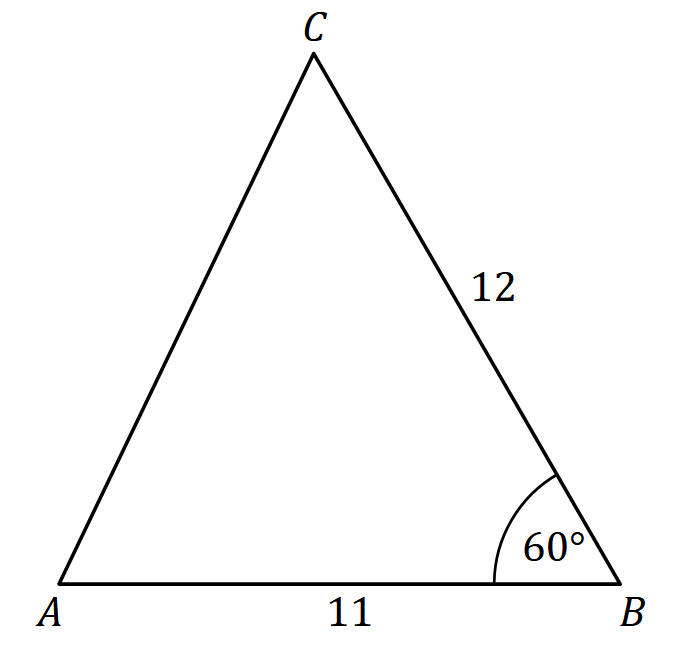

Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, albo F – jeśli jest fałszywe.
| Trójkąt \(ABC\) jest równoramienny. | P | F |
| Pole trójkąta \(ABC\) jest równe \(33\sqrt{3}\). | P | F |
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
W kartezjańskim układzie współrzędnych \((x, y)\) dany jest kwadrat \(ABCD\), w którym \(A=(4,-1)\). Przekątne tego kwadratu przecinają się w punkcie \(S=(1,3)\). Przekątna kwadratu \(ABCD\) ma długość A.\(5\)
B.\(7\)
C.\(10\)
D.\(14\)
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
W kartezjańskim układzie współrzędnych \((x, y)\) proste \(k\) oraz \(l\) są określone równaniami \[ \begin{aligned} k:&\; y=(m-2)\,x+5\\ l:&\; y=-4\,x+(m+3) \end{aligned} \] Proste \(k\) oraz \(l\) są równoległe, gdy liczba \(m\) jest równa A.\((-4)\)
B.\((-2)\)
C.\(2\)
D.\(5\)
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
W kartezjańskim układzie współrzędnych \((x, y)\) punkt \(P=(0,0)\) leży na okręgu \(\mathcal{O}\) o środku w punkcie \(S=(2,4)\). Okrąg \(\mathcal{O}\) jest określony równaniem A.\((x-2)^{2}+(y-4)^{2}=2\sqrt{5}\)
B.\((x-2)^{2}+(y-4)^{2}=20\)
C.\((x+2)^{2}+(y+4)^{2}=2\sqrt{5}\)
D.\((x+2)^{2}+(y+4)^{2}=20\)
Tworząca stożka ma długość \(8\). Kąt rozwarcia tego stożka ma miarę \(120^{\circ}\).
Oblicz objętość tego stożka. Zapisz obliczenia.
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Objętość sześcianu jest równa \(729\). Długość przekątnej tego sześcianu jest równa A.\(9\sqrt{3}\)
B.\(9\sqrt{2}\)
C.\(3\sqrt{3}\)
D.\(3\sqrt{2}\)
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Wszystkich liczb naturalnych trzycyfrowych nieparzystych, w których zapisie dziesiętnym występuje dokładnie jeden raz cyfra \(0\), jest A.\(45\)
B.\(50\)
C.\(54\)
D.\(81\)
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Doświadczenie losowe polega na dwukrotnym rzucie symetryczną sześcienną kostką do gry, która na każdej ściance ma inną liczbę oczek – od 1 do 6. Zdarzenie \(A\) polega na tym, że suma liczb wyrzuconych oczek będzie równa \(11\). Prawdopodobieństwo zdarzenia \(A\) jest równe A.\(\dfrac{1}{36}\)
B.\(\dfrac{6}{36}\)
C.\(\dfrac{11}{36}\)
D.\(\dfrac{2}{36}\)
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Średnia arytmetyczna siedmiu liczb: \(1,\,2,\,3,\,4,\,5,\,x,\,y\) jest równa \(3\). Suma \(x+y\) jest równa A.\(4\)
B.\(5\)
C.\(6\)
D.\(7\)
Na diagramie przedstawiono wyniki sprawdzianu z matematyki w pewnej klasie maturalnej liczącej \(24\) uczniów. Na osi poziomej podano oceny, które uzyskali uczniowie tej klasy, a na osi pionowej podano liczbę uczniów, którzy otrzymali daną ocenę. 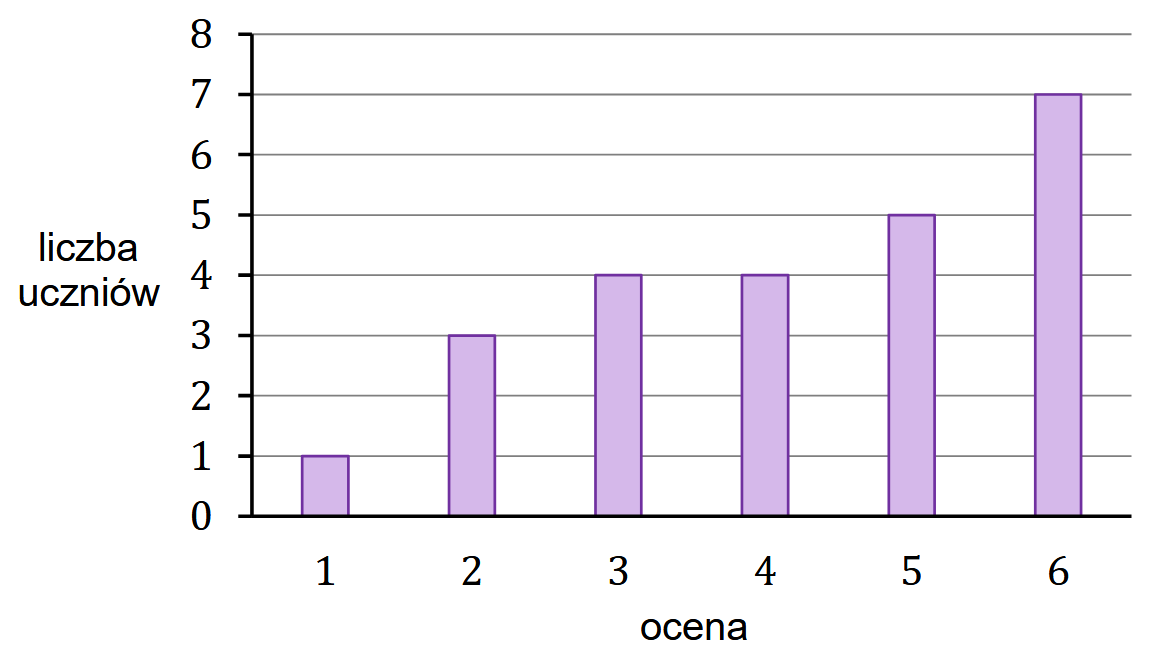

Uzupełnij zdania. Wpisz odpowiednie liczby w wykropkowanych miejscach, aby zdania były prawdziwe.
- Mediana ocen uzyskanych \(z\) tego sprawdzianu przez uczniów tej klasy jest równa ......... .
- Dominanta ocen uzyskanych \(z\) tego sprawdzianu przez uczniów tej klasy jest równa ......... .
Rozważamy wszystkie prostopadłościany \(A B C D E F G H\), w których krawędź \(BC\) ma długość \(4\) oraz suma długości wszystkich krawędzi wychodzących z wierzchołka \(B\) jest równa \(15\) (zobacz rysunek). 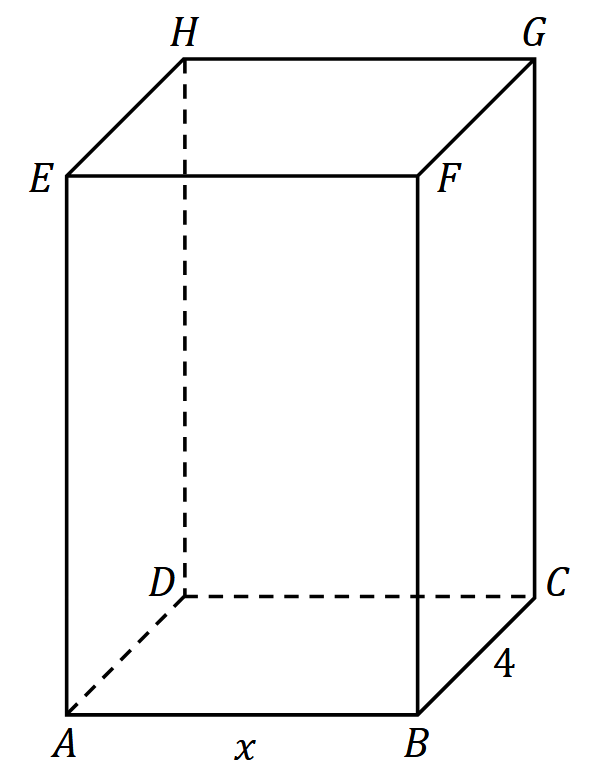 Niech \(P(x)\) oznacza funkcję pola powierzchni całkowitej takiego prostopadłościanu w zależności od długości \(x\) krawędzi \(AB\).
Niech \(P(x)\) oznacza funkcję pola powierzchni całkowitej takiego prostopadłościanu w zależności od długości \(x\) krawędzi \(AB\).
 Niech \(P(x)\) oznacza funkcję pola powierzchni całkowitej takiego prostopadłościanu w zależności od długości \(x\) krawędzi \(AB\).
Niech \(P(x)\) oznacza funkcję pola powierzchni całkowitej takiego prostopadłościanu w zależności od długości \(x\) krawędzi \(AB\). Wyznacz wzór i dziedzinę funkcji \(P\). Oblicz długość \(x\) krawędzi \(AB\) tego z rozważanych prostopadłościanów, którego pole powierzchni całkowitej jest największe. Zapisz obliczenia.