Matura podstawowa 2025 - czerwiec - termin dodatkowy
Poziom podstawowy
Pliki do pobrania: Arkusz można też wydrukować w prawym górnym rogu strony według własnych preferencji.
Liczby \(\,x_{1}\) i \(x_{2}\) są różnymi rozwiązaniami równania \(\lvert x-6\rvert = 4\).
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Iloczyn \(x_{1}\cdot x_{2}\) jest równy A.\(4\)
B.\(20\)
C.\(24\)
D.\(100\)
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Liczba \(256\cdot \sqrt[3]{8^2}\) jest równa A.\(2^8\)
B.\(2^{10}\)
C.\(2^{16}\)
D.\(2^{36}\)
Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, albo F – jeśli jest fałszywe.
| Iloczyn \(2\cdot\log_{3}5\) jest równy \(\log_{3}25\). | P | F |
| Suma \(2+\log_{3}5\) jest równa \(\log_{3}10\). | P | F |
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Liczba \(\bigl(\sqrt{3}+1\bigr)^{2}-\sqrt{12}\) jest równa A.\(4-4\sqrt{3}\)
B.\(4-2\sqrt{3}\)
C.\(2\)
D.\(4\)
Wykaż, że dla każdej liczby całkowitej \(a\), która przy dzieleniu przez \(5\) daje resztę \(1\), i dla każdej liczby całkowitej \(b\), która przy dzieleniu przez \(5\) daje resztę \(4\), liczba \(a^{2}-b^{2}\) jest podzielna przez \(5\).
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Dana jest nierówność \[ 8-\frac{1-2x}{2}\ge 3x. \] Największą liczbą całkowitą, która spełnia tę nierówność, jest A.\(1\)
B.\(2\)
C.\(3\)
D.\(4\)
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Równanie \(4\bigl(x-1\bigr)^{2}\bigl(x^{2}-25\bigr)=0\) w zbiorze liczb rzeczywistych ma dokładnie A. dwa rozwiązania.
B. trzy rozwiązania.
C. cztery rozwiązania.
D. pięć rozwiązań.
W maju \(2024\) roku założono dwa sady: posadzono w nich łącznie \(1410\) drzew.
Po roku stwierdzono, że uschło \(20\%\) drzew w pierwszym sadzie i \(15\%\) drzew w drugim sadzie. Uschnięte drzewa usunięto, a nowych nie dosadzano.
Liczba drzew, które pozostały w drugim sadzie, stanowiła \(70\%\) liczby drzew, które pozostały w pierwszym sadzie.
Po roku stwierdzono, że uschło \(20\%\) drzew w pierwszym sadzie i \(15\%\) drzew w drugim sadzie. Uschnięte drzewa usunięto, a nowych nie dosadzano.
Liczba drzew, które pozostały w drugim sadzie, stanowiła \(70\%\) liczby drzew, które pozostały w pierwszym sadzie.
Oblicz, ile drzew posadzono w pierwszym sadzie w maju \(2024\) roku. Zapisz obliczenia.
Rozwiąż nierówność \[ x(x+4)\lt x-2. \] Zapisz obliczenia.
Funkcja \(f\) jest określona następująco: \[ f(x)= \begin{cases} -x-2 & \text{dla } x\in(-5,-2],\\ 0 & \text{dla } x\in(-2,1],\\ x & \text{dla } x\in(1,3]. \end{cases} \] Wykres funkcji \(y=f(x)\) przedstawiono w kartezjańskim układzie współrzędnych \((x,y)\) na rysunku poniżej. 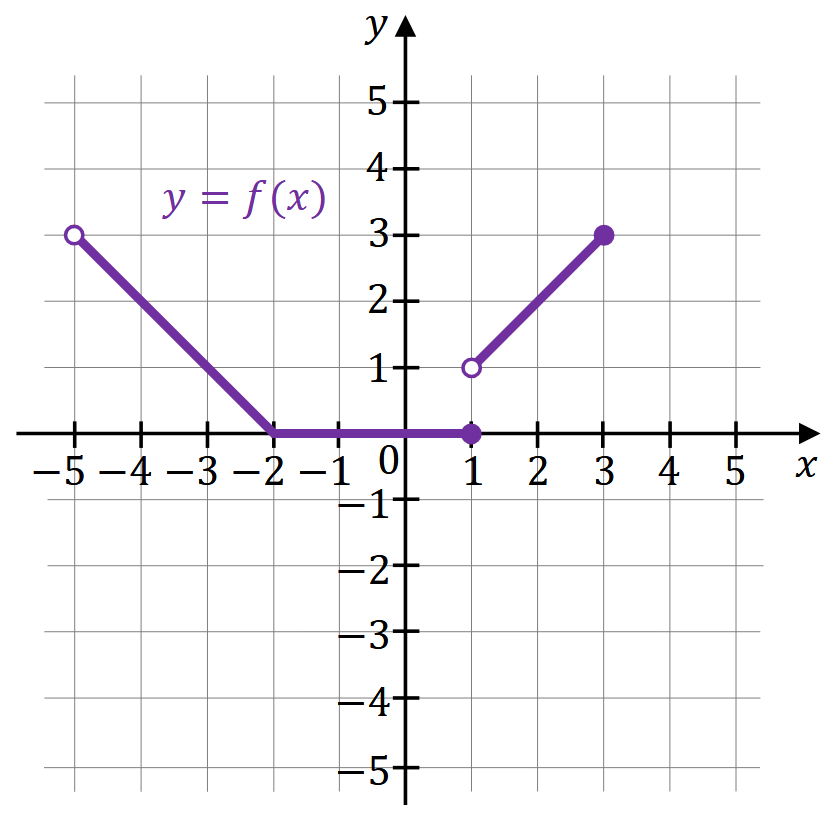

Uzupełnij zdania. Wpisz odpowiednie przedziały w wykropkowanych miejscach, aby zdania były prawdziwe.
- Dziedziną funkcji \(f\) jest przedział ……………… .
- Zbiorem wartości funkcji \(f\) jest przedział ……………… .
- Zbiorem wszystkich miejsc zerowych funkcji \(f\) jest przedział ……………… .
- Zbiorem wszystkich rozwiązań nierówności \(f(x)\lt f(-3)\) jest przedział ……………… .
Funkcja liniowa \(f\) jest określona wzorem \(f(x)=\frac12 x-k\), gdzie \(k\) jest liczbą rzeczywistą. Miejsce zerowe funkcji \(f\) jest liczbą większą od \(2\).
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Liczba \(k\) należy do przedziału A.\((-\infty,-1)\)
B.\((-1,0)\)
C.\((0,1)\)
D.\((1,+\infty)\)
Funkcja liniowa \(f\) jest określona wzorem \(f(x)=5 x\). W kartezjańskim układzie współrzędnych ( \(x, y\) ) wykres funkcji \(f\) przesunięto o jedną jednostkę w prawo wzdłuż osi \(O x\) i w wyniku tego przesunięcia otrzymano wykres funkcji liniowej \(g\).
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Funkcja \(g\) jest określona wzorem A.\(g(x)=5x-5\)
B.\(g(x)=5x-1\)
C.\(g(x)=5x+1\)
D.\(g(x)=5x+5\)
W kartezjańskim układzie współrzędnych \((x,y)\) wykres funkcji kwadratowej \(f\) przechodzi przez punkt \((2,15)\). Osią symetrii tego wykresu jest prosta \(x=-1\). Jednym z miejsc zerowych funkcji \(f\) jest liczba \(1\).
Wyznacz wzór funkcji \(f\) w postaci kanonicznej. Zapisz obliczenia.
Ciąg \(\left(a_{n}\right)\) jest określony wzorem \(a_{n}=3 n^{2}-3 n\) dla każdej liczby naturalnej \(n \geq 1\).
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Suma \(S_{3}\) trzech początkowych kolejnych wyrazów tego ciągu jest równa A.\(18\)
B.\(24\)
C.\(60\)
D.\(90\)
Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, albo F – jeśli jest fałszywe.
| Ciąg \((a_{n})\) jest arytmetyczny. | P | F |
| Wszystkie wyrazy ciągu \((a_{n})\) są liczbami parzystymi. | P | F |
W ciągu arytmetycznym \(\left(a_{n}\right)\), określonym dla każdej liczby naturalnej \(n \geq 1\), dane są wyrazy: \(a_{1}=52\) oraz \(a_{25}=2\).
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Różnica ciągu \((a_{n})\) jest równa A.\(\left(-\frac{25}{12}\right)\)
B.\((-2)\)
C.\(2\)
D.\(\displaystyle\frac{25}{12}\)
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Suma \(S_{25}\) dwudziestu pięciu początkowych kolejnych wyrazów ciągu \((a_{n})\) jest równa A.\(675\)
B.\(700\)
C.\(1300\)
D.\(1325\)
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Trzywyrazowy ciąg \((4,\,m,\,m-1)\) jest geometryczny, gdy liczba \(m\) jest równa A.\((-3)\)
B.\((-2)\)
C.\(2\)
D.\(3\)
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Liczba \(\dfrac{\sin^{3}25^{\circ}+\sin25^{\circ}\cos^{2}25^{\circ}}{\cos25^{\circ}}\) jest równa A.\(\sin25^{\circ}\)
B.\(\cos25^{\circ}\)
C.\(\tan25^{\circ}\)
D.\(1\)
Dany jest trójkąt prostokątny o kątach ostrych \(\alpha\) oraz \(\beta\) (zobacz rysunek). Sinus kąta \(\alpha\) jest równy \(\frac{4}{7}\). 

Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, albo F – jeśli jest fałszywe.
| Cosinus kąta \(\alpha\) jest równy \(\frac37\). | P | F |
| Cosinus kąta \(\beta\) jest równy \(\frac47\). | P | F |
Dany jest trójkąt prostokątny o bokach długości \(10,\,24,\,26\) (zobacz rysunek). 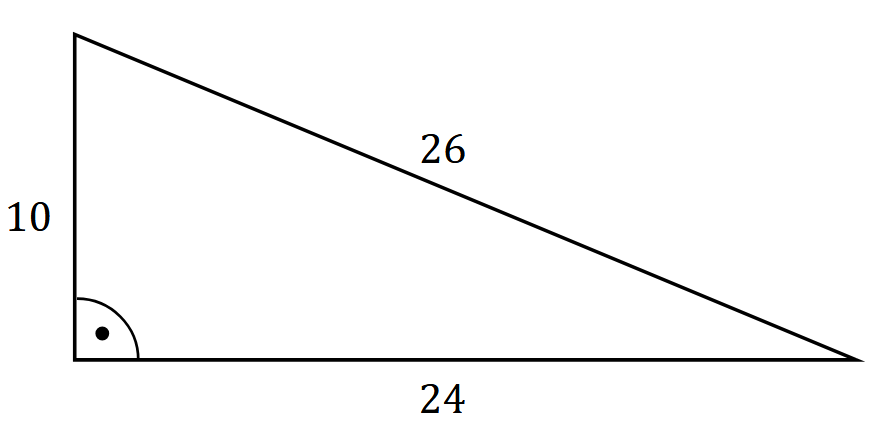

Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Długość promienia okręgu wpisanego w ten trójkąt jest równa A.\(\dfrac{10}{3}\)
B.\(4\)
C.\(5\)
D.\(\dfrac{80}{13}\)
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Długość promienia okręgu opisanego na tym trójkącie jest równa A.\(\dfrac{80}{13}\)
B.\(\dfrac{20}{3}\)
C.\(12\)
D.\(13\)
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Na dziesięciokącie foremnym \(ABCDEFGHIJ\) opisano okrąg o środku \(S\). 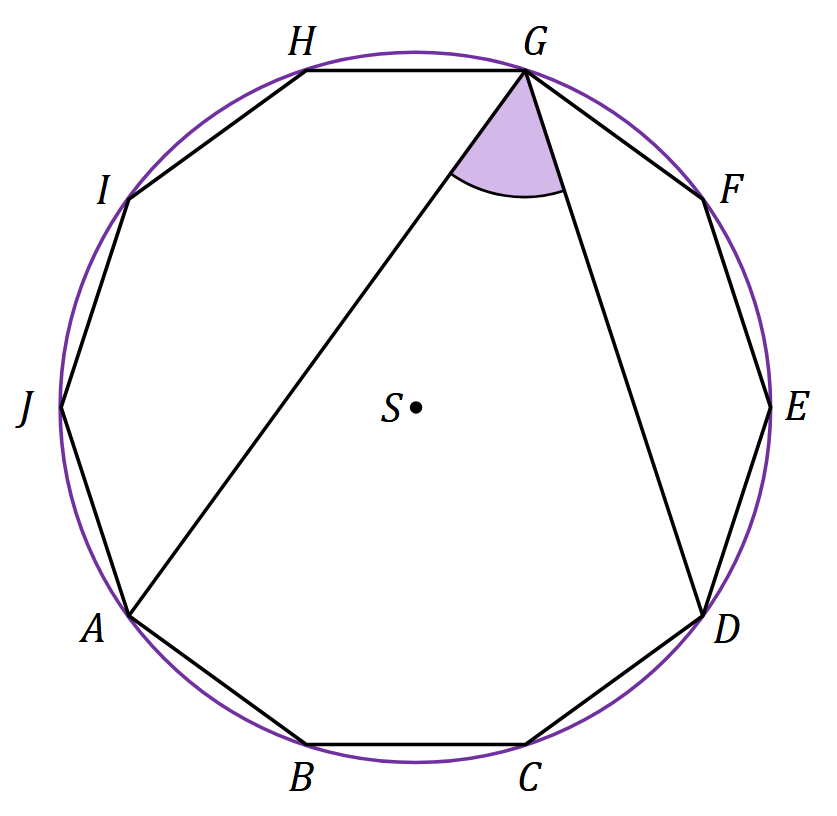 Miara kąta wpisanego \(AGD \) jest równa
Miara kąta wpisanego \(AGD \) jest równa A.\(18^{\circ}\)
B.\(36^{\circ}\)
C.\(54^{\circ}\)
D.\(60^{\circ}\)
Kwadrat \(\mathcal{K}_{2}\) jest podobny do kwadratu \(\mathcal{K}_{1}\) w skali \(5\) (zobacz rysunek). Suma pól tych kwadratów jest równa \(78\). 

Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Długość boku kwadratu \(\mathcal{K}_{1}\) jest równa A.\(\sqrt{3}\)
B.\(3\)
C.\(\sqrt{13}\)
D.\(13\)
W układzie współrzędnych \((x,y)\) dana jest prosta \(k\!: y=5x+7\). Prosta \(l\) jest równoległa do \(k\) i przecina oś \(Oy\) w punkcie \((0,-4)\).
Punkt o współrzędnych \((p,2)\) należy do prostej \(l\).
Punkt o współrzędnych \((p,2)\) należy do prostej \(l\).
Oblicz \(p\). Zapisz obliczenia.
W kartezjańskim układzie współrzędnych \((x, y)\) dany jest okrąg \(\mathcal{O}\) o równaniu \[ \mathcal{O}:(x+1)^{2}+(y-2)^{2}=9 \] Okrąg \(\mathcal{K}\) jest obrazem okręgu \(\mathcal{O}\) w symetrii osiowej względem osi \(O y\) układu współrzędnych.
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Okrąg \(\mathcal{K}\) jest określony równaniem A.\((x+1)^{2}+(y+2)^{2}=9\)
B.\((x+1)^{2}+(y-2)^{2}=9\)
C.\((x-1)^{2}+(y+2)^{2}=9\)
D.\((x-1)^{2}+(y-2)^{2}=9\)
Pole powierzchni całkowitej prostopadłościanu jest równe \(94{,}5\).
Długości trzech krawędzi wychodzących z tego samego wierzchołka tworzą ciąg geometryczny o ilorazie równym \(4\).
Długości trzech krawędzi wychodzących z tego samego wierzchołka tworzą ciąg geometryczny o ilorazie równym \(4\).
Oblicz objętość tego prostopadłościanu. Zapisz obliczenia.
Pole powierzchni całkowitej ostrosłupa prawidłowego czworokątnego jest równe \(20\). Pole powierzchni bocznej tego ostrosłupa jest cztery razy większe od pola jego podstawy.
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Długość krawędzi podstawy tego ostrosłupa jest równa A.\(2\)
B.\(\sqrt{5}\)
C.\(\sqrt{10}\)
D.\(4\)
Tworząca stożka ma długość \(6\). Kąt rozwarcia stożka ma miarę \(60^{\circ}\).
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Wysokość tego stożka jest równa A.\(3\)
B.\(2\sqrt{3}\)
C.\(3\sqrt{3}\)
D.\(3\sqrt{5}\)
Dane są dwa zbiory: \(X=\{-3,-2,-1,0,1,2\}\) oraz \(Y=\{-2,-1,0,1\}\). Losujemy jedną liczbę ze zbioru \(X\), a następnie losujemy jedną liczbę ze zbioru \(Y\) i tworzymy uporządkowaną parę liczb ( \(x, y\) ), gdzie \(x\) jest liczbą wylosowaną ze zbioru \(X\) oraz \(y\) jest liczbą wylosowaną ze zbioru \(Y\).
Oblicz prawdopodobieństwo zdarzenia \(A\) polegającego na tym, że wylosujemy parę liczb ( \(\boldsymbol{x}, \boldsymbol{y}\) ), która będzie spełniać warunek \(\boldsymbol{x} \cdot \boldsymbol{y} \geq \mathbf{0}\). Zapisz obliczenia.
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Wszystkich liczb naturalnych trzycyfrowych parzystych, w których zapisie dziesiętnym występuje dokładnie jeden raz cyfra \(0\), jest A.\(108\)
B.\(117\)
C.\(126\)
D.\(162\)
Średnia arytmetyczna trzech liczb: \(a, b, c\), jest równa 12 .
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Średnia arytmetyczna sześciu liczb: \(2 a, 3 a, 2 b, 3 b, 2 c, 3 c\), jest równa A.\(10\)
B.\(12\)
C.\(30\)
D.\(60\)
W tabeli zestawiono liczbę punktów uzyskanych przez \(32\) uczniów pewnej klasy za rozwiązanie jednego z zadań ze sprawdzianu z matematyki. 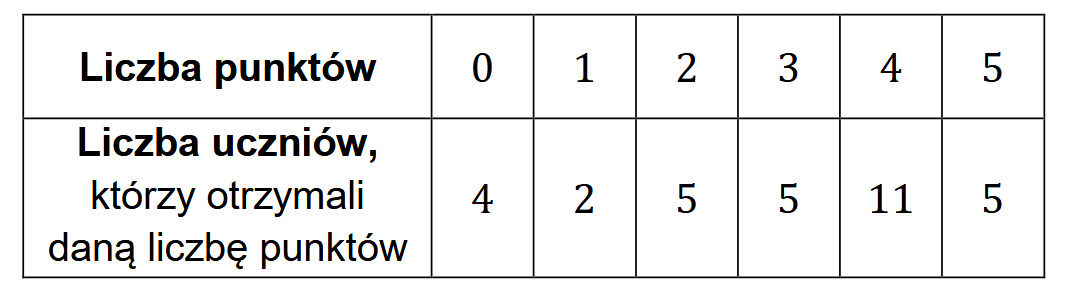

Uzupełnij zdania. Wpisz odpowiednie liczby w wykropkowanych miejscach, aby zdania były prawdziwe.
- Wynik niższy od średniej arytmetycznej liczby punktów otrzymanych przez tych uczniów za rozwiązanie tego zadania uzyskało dokładnie …………… uczniów tej klasy.
- Mediana liczby punktów otrzymanych przez tych uczniów za rozwiązanie tego zadania jest równa …………… .
- Dominanta liczby punktów otrzymanych przez tych uczniów za rozwiązanie tego zadania jest równa …………… .
Producent latarek przeanalizował wpływ zmiany ceny latarki L25 na liczbę kupujących ten produkt. Z analizy wynika, że roczny zysk \(Z\) ze sprzedaży latarek L25 wyraża się wzorem \[ Z(x)=(500+50 x)(16-x) \] gdzie:
\(x\) - kwota obniżki ceny latarki L25 (wyrażona w pełnych złotych), spełniająca warunki \(x \geq 1\) i \(x \leq 14\),
\(Z\) - roczny zysk ze sprzedaży latarek L25 (wyrażony w złotych), liczony od momentu obniżenia ceny.
\(x\) - kwota obniżki ceny latarki L25 (wyrażona w pełnych złotych), spełniająca warunki \(x \geq 1\) i \(x \leq 14\),
\(Z\) - roczny zysk ze sprzedaży latarek L25 (wyrażony w złotych), liczony od momentu obniżenia ceny.
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Roczny zysk \(Z\) ze sprzedaży latarek L25 będzie największy dla \(x\) równego A.\(3\)
B.\(4\)
C.\(7\)
D.\(14\)
Tematy nadrzędne i sąsiednie