Monotoniczność funkcji

Drukuj

Poziom podstawowy

Na potrzeby poniższych definicji zakładamy, że argumenty \(x_1\) oraz \(x_2\) należą do dziedziny funkcji \(f\).

Definicja

Funkcja \(f\) jest rosnąca jeżeli dla dowolnych dwóch argumentów \(x_1\) oraz \(x_2\) takich, że \(x_1 \lt x_2\), zachodzi warunek \(f(x_1) \lt f(x_2)\).

Przykłady funkcji rosnących: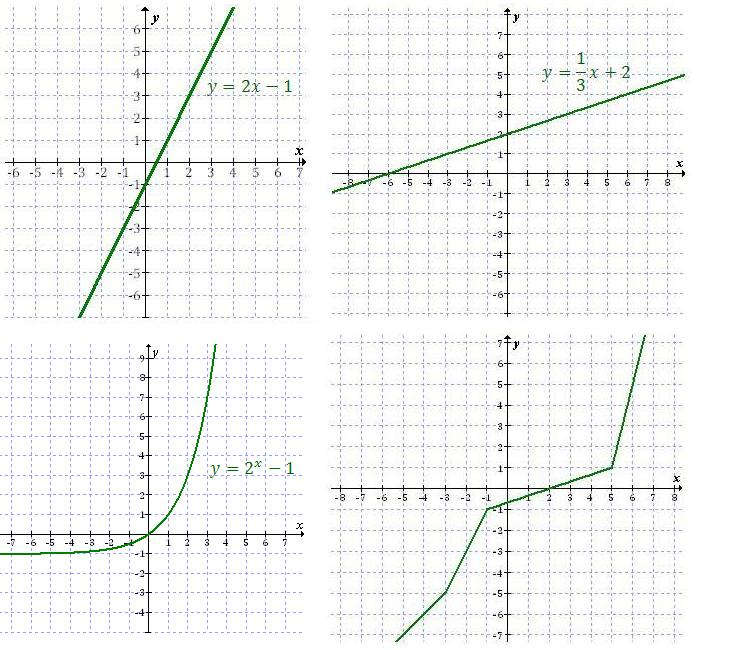

Wykaż, że funkcja \(f: \mathbb{R} \rightarrow \mathbb{R} \) dana wzorem \(f(x)=\frac{1}{3}x-5\) jest rosnąca.

Weźmy dwa argumenty \(x_1,x_2\in \mathbb{R} \), takie, że \(x_1\lt x_2\). Wystarczy pokazać, że \(f(x_1)\lt f(x_2)\). Przekształcamy nierówność do nierówności równoważnych: \[\begin{split} f(x_1)&\lt f(x_2)\\[6pt] \frac{1}{3}x_1-5 &\lt \frac{1}{3}x_2-5\quad /+5\\[6pt] \frac{1}{3}x_1 &\lt \frac{1}{3}x_2\quad /\cdot 3 \\[6pt] x_1 &\lt x_2 \end{split}\] Otrzymaliśmy nierówność prawdziwą, zetem wykazaliśmy, że funkcja \(f\) jest rosnąca.

Definicja

Funkcja \(f\) jest malejąca jeżeli dla dowolnych dwóch argumentów \(x_1\) oraz \(x_2\) takich, że \(x_1 \lt x_2\), zachodzi warunek \(f(x_1) \gt f(x_2)\).

Przykłady funkcji malejących: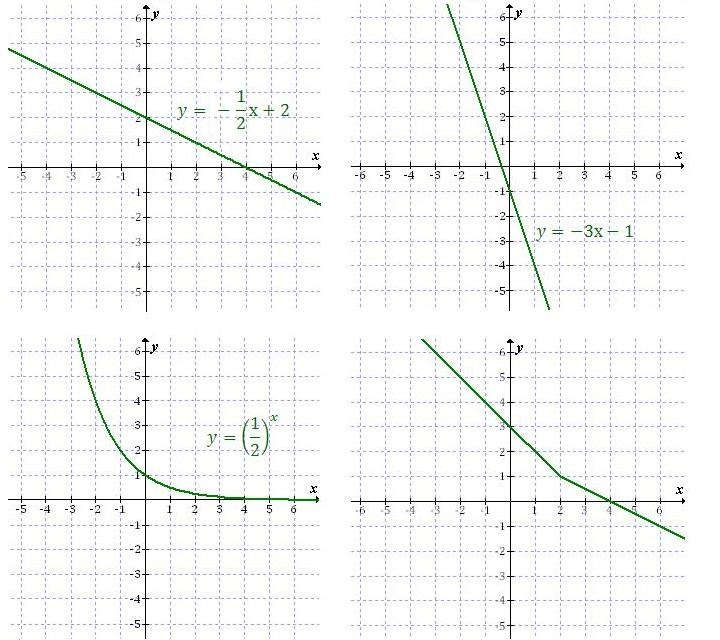

Wykaż, że funkcja \(f: (0, +\infty ) \rightarrow \mathbb{R} \) dana wzorem \(f(x)=\frac{2}{x}+5\) jest malejąca.

Weźmy dwa argumenty \(x_1,x_2\in \mathbb{R} \), takie, że \(x_1\lt x_2\). Wystarczy pokazać, że \(f(x_1)\gt f(x_2)\). Przekształcamy nierówność do nierówności równoważnych: \[\begin{split} f(x_1)&\gt f(x_2)\\[6pt] \frac{2}{x_1}+5 &\gt \frac{2}{x_2}+5\quad /-5\\[6pt] \frac{2}{x_1} &\gt \frac{2}{x_2}\quad /\cdot x_1x_2 \\[6pt] 2x_2 &\gt 2x_1\quad /: 2 \\[6pt] x_2 &\gt x_1\\[6pt] x_1 &\lt x_2 \end{split}\] Otrzymaliśmy nierówność prawdziwą, zetem wykazaliśmy, że funkcja \(f\) jest malejąca.

Definicja

Funkcja \(f\) jest stała, jeżeli dla każdego argumentu z dziedziny przyjmuje taką samą wartość.

Wykresem funkcji stałej jest linia prosta równoległa do osi \(x\)-ów.

Przykładowe wykresy funkcji stałych: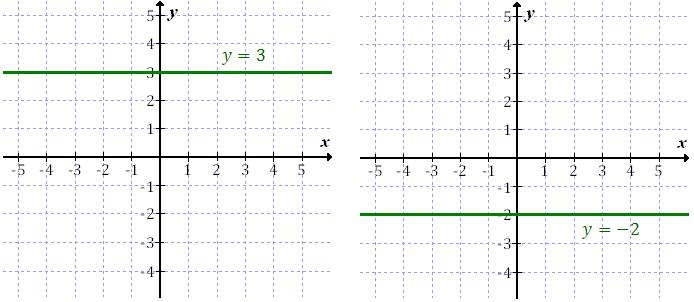

Definicja

Funkcja \(f\) jest nierosnącą jeżeli dla dowolnych dwóch argumentów \(x_1\) oraz \(x_2\) takich, że \(x_1 \lt x_2\), zachodzi warunek \(f(x_1) \ge f(x_2)\).
Czyli funkcja jest nierosnącą kiedy jest malejąca lub stała.

Przykład funkcji nierosnącej: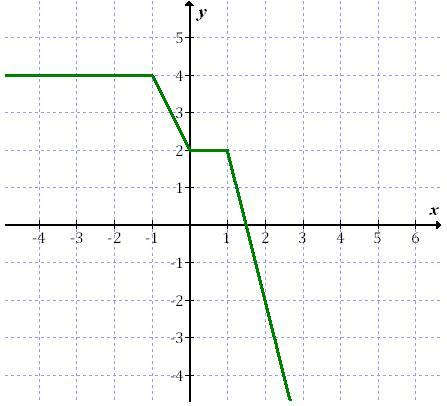

Definicja

Funkcja \(f\) jest niemalejąca jeżeli dla dowolnych dwóch argumentów \(x_1\) oraz \(x_2\) takich, że \(x_1 \lt x_2\), zachodzi warunek \(f(x_1) \le f(x_2)\).
Czyli funkcja jest niemalejąca kiedy jest rosnąca lub stała.

Przykładowy wykres funkcji niemalejącej: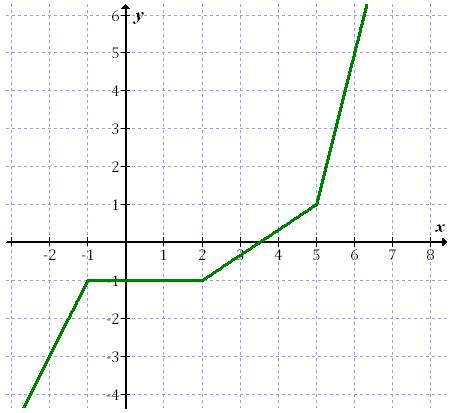

Definicja

Funkcja jest monotoniczna, jeżeli jest rosnąca, malejąca, niemalejąca, nierosnąca albo stała.

Definicja

Funkcję nazywamy niemonotoniczną, gdy na pewnych przedziałach jest rosnąca, a na pewnych malejąca.
W takim przypadku można ewentualnie mówić, że funkcja jest monotoniczna przedziałami.

Przykłady funkcji niemonotonicznych:

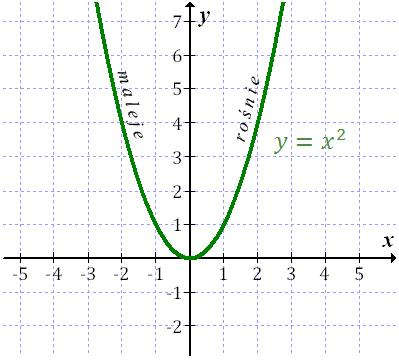
Funkcja \(f(x) = x^2\) nie jest monotoniczna. Jest malejąca w przedziale \((-\infty ;0\rangle \) a rosnąca w przedziale \(\langle 0;+\infty )\).
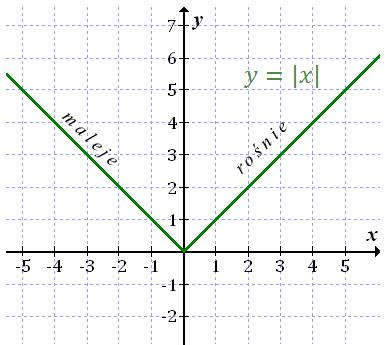
Funkcja \(f(x) = |x|\) nie jest monotoniczna. Jest malejąca w przedziale \((-\infty, 0\rangle\), a rosnąca w przedziale \(\langle 0, +\infty)\).
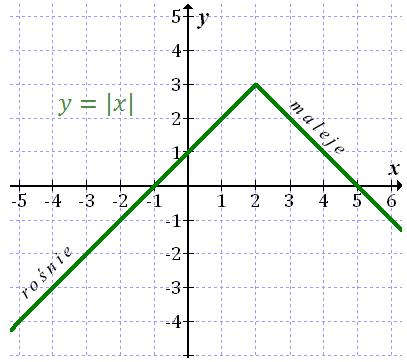
Funkcja \(f(x) = -|x - 2| + 3\) nie jest monotoniczna. Jest rosnąca w przedziale \((-\infty, 2\rangle\), a malejąca w przedziale \(\langle 2, +\infty )\).

W tym filmiku wyjaśniam co to jest monotoniczność funkcji oraz pokazuję jak badać monotoniczność funkcji danych wzorem.

Czas nagrania: 20 min.