Interpretacja geometryczna liczby zespolonej
Poziom studiów
W rozdziale Definicja powiedzieliśmy, że każdej liczbie zespolonej \(z=a+bi\) odpowiada uporządkowana para liczb \((a,b)\). Przykłady zapisania liczby zespolonej na dwa różne sposoby.
| Liczba zespolona zapisana w postaci ogólnej | Liczba zespolona zapisana jako punkt |
| \(a + bi\) | \((a, b)\) |
| \(2 + 5i\) | \((2, 5)\) |
| \(5 + 2i\) | \((5, 2)\) |
| \(7 - i\) | \((7, -1)\) |
| \(-8 - 2i\) | \((-8, -2)\) |
| \(i\) | \((0, 1)\) |
| \(1\) | \((1, 0)\) |
| \(0\) | \((0, 0)\) |
Możemy interpretować liczby zespolone jako punkty na płaszczyźnie.
Na osi \(x\)-ów będziemy zaznaczać część rzeczywistą liczby zespolonej, a na osi \(y\)-ów część urojoną.
Na osi \(x\)-ów będziemy zaznaczać część rzeczywistą liczby zespolonej, a na osi \(y\)-ów część urojoną.
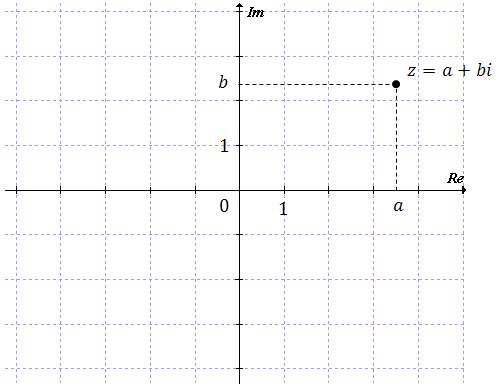 Oto przykłady kilku konkretnych liczb zespolonych zaznaczonych w układzie współrzędnych:
Oto przykłady kilku konkretnych liczb zespolonych zaznaczonych w układzie współrzędnych: 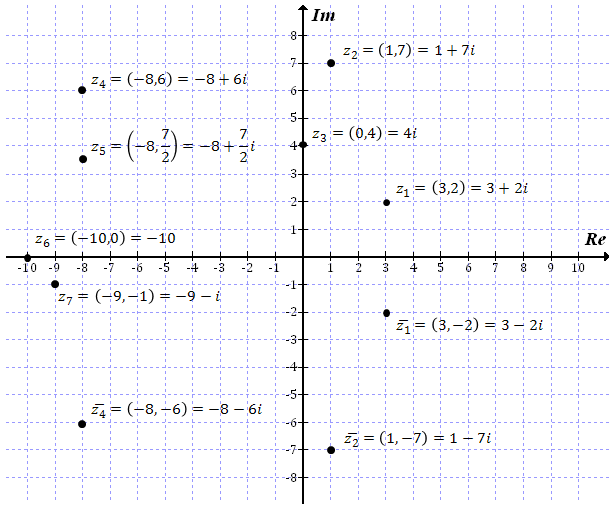
W powyższym układzie współrzędnych zaznaczyłem również liczby sprzężone do \(z_1\), \(z_2\) oraz \(z_4\). Zauważ, że są one po prostu odbiciami symetrycznymi względem osi \(x\)-ów.
Zaznaczymy teraz jeden ogólny punkt na płaszczyźnie zespolonej i określimy dla niego kilka własności.
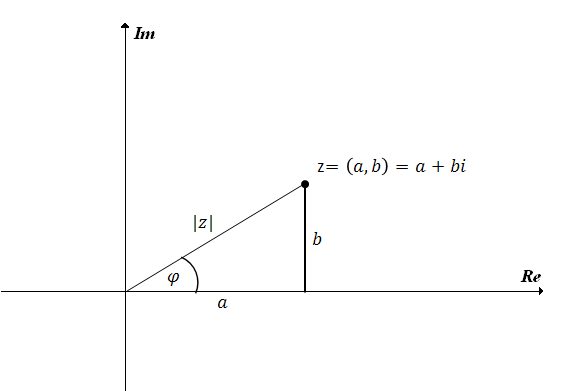

Odległość liczby zespolonej \(z=a+bi\) od początku układu współrzędnych, z twierdzenia Pitagorasa, wyraża się wzorem: 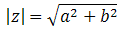 Czyli jest to po prostu moduł tej liczby \(z\).
Czyli jest to po prostu moduł tej liczby \(z\).
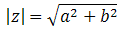 Czyli jest to po prostu moduł tej liczby \(z\).
Czyli jest to po prostu moduł tej liczby \(z\). Kąt między osią Re, a półprostą wychodzącą z początku układu współrzędnych i przechodzącą przez punkt \(z\) oznaczamy najczęściej literką \(\varphi\) (czytamy: fi).
Miarę zaznaczonego kąta \(\varphi\) będziemy zazwyczaj wyrażać w radianach (a nie w stopniach). Możemy zatem napisać, że \(\varphi\in \mathbb{R} \).
Liczbę \(\varphi\) nazywamy argumentem liczby \(z\) i oznaczamy \(\operatorname{arg} z\).Dla liczby \(z\) którą zaznaczyliśmy w powyższym układzie współrzędnych mamy: \[\operatorname{arg} z = \varphi \] Korzystając wprost z definicji funkcji trygonometrycznych dla trójkąta prostokątnego narysowanego w powyższym układzie współrzędnych, otrzymujemy:
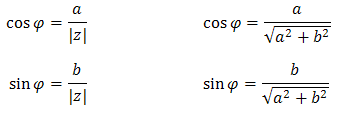 Wzory po prawej stronie otrzymaliśmy z tych po lewej, po prostu podstawiając do nich wzór na moduł. Dla wygody dalej będziemy posługiwali się głównie tymi wzorami po lewej (bo są krótsze w zapisie). Bezpośrednio z nich otrzymujemy, że:
Wzory po prawej stronie otrzymaliśmy z tych po lewej, po prostu podstawiając do nich wzór na moduł. Dla wygody dalej będziemy posługiwali się głównie tymi wzorami po lewej (bo są krótsze w zapisie). Bezpośrednio z nich otrzymujemy, że: 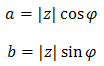
Możemy zatem zapisać, że: 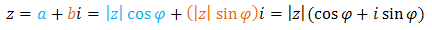
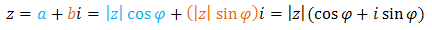
Wzór który otrzymaliśmy: 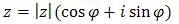 to postać trygonometryczna liczby zespolonej \(z=a+bi\).
to postać trygonometryczna liczby zespolonej \(z=a+bi\).
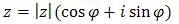 to postać trygonometryczna liczby zespolonej \(z=a+bi\).
to postać trygonometryczna liczby zespolonej \(z=a+bi\). Wiemy już, że możemy przedstawić jedną liczbę zespoloną na trzy różne sposoby:
- w postaci ogólnej \(z=a+bi\),
- jako punkt \((a,b)\) na płaszczyźnie,
- w postaci trygonometrycznej \(z=|z|(\cos \varphi + i\sin \varphi)\).
Każda z nich ma swoje plusy i minusy. Zaletą postaci trygonometrycznej jest to, że umożliwia w łatwy sposób podnoszenie liczb zespolonych do dużych potęg. Więcej na ten temat powiemy w rozdziale Wzór de Moivre'a - potęgowanie liczb zespolonych.
Dla liczby zespolonej\(z=\sqrt{3}+i\) wyznacz moduł, argument oraz postać trygonometryczną.
Zacznijmy od zaznaczenia liczby \(z\) w układzie współrzędnych: 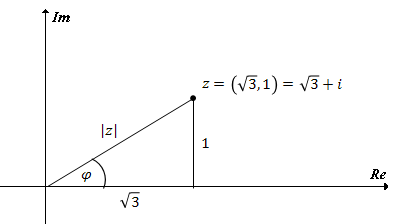 Obliczamy moduł z twierdzenia Pitagorasa:
Obliczamy moduł z twierdzenia Pitagorasa: 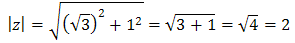 Teraz obliczamy argument, np. korzystając z definicji sinusa:
Teraz obliczamy argument, np. korzystając z definicji sinusa: 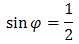 Zatem:
Zatem: 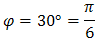 Możemy nawet zapisać, że:
Możemy nawet zapisać, że: 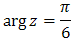 Teraz zapisujemy postać trygonometryczną, podstawiając do wzoru wyliczone przed chwilą wartości:
Teraz zapisujemy postać trygonometryczną, podstawiając do wzoru wyliczone przed chwilą wartości: 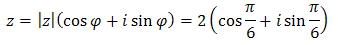 Możemy jeszcze sprawdzić, że obliczając wartości liczbowe funkcji trygonometrycznych w powyższym wzorze, otrzymamy wyjściową postać ogólną:
Możemy jeszcze sprawdzić, że obliczając wartości liczbowe funkcji trygonometrycznych w powyższym wzorze, otrzymamy wyjściową postać ogólną: 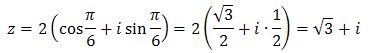
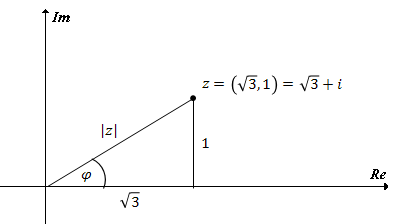 Obliczamy moduł z twierdzenia Pitagorasa:
Obliczamy moduł z twierdzenia Pitagorasa: 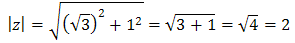 Teraz obliczamy argument, np. korzystając z definicji sinusa:
Teraz obliczamy argument, np. korzystając z definicji sinusa: 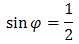 Zatem:
Zatem: 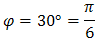 Możemy nawet zapisać, że:
Możemy nawet zapisać, że: 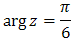 Teraz zapisujemy postać trygonometryczną, podstawiając do wzoru wyliczone przed chwilą wartości:
Teraz zapisujemy postać trygonometryczną, podstawiając do wzoru wyliczone przed chwilą wartości: 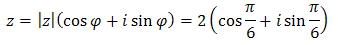 Możemy jeszcze sprawdzić, że obliczając wartości liczbowe funkcji trygonometrycznych w powyższym wzorze, otrzymamy wyjściową postać ogólną:
Możemy jeszcze sprawdzić, że obliczając wartości liczbowe funkcji trygonometrycznych w powyższym wzorze, otrzymamy wyjściową postać ogólną: 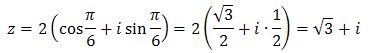
Tematy nadrzędne i sąsiednie