Zestaw treningowy 3

Drukuj

Poziom podstawowy

Dana jest funkcja \(f(x)=\frac{x^2+2}{1-b}\). Oblicz współczynnik \(b\) jeżeli wiadomo, że \(f(2) = -3\).

\(b=3\)

Dana jest funkcja \(f(x) = (1 + m^2)x - 5\). Oblicz współczynnik \(m\) jeżeli wiadomo, że \(x = 1\) jest miejscem zerowym funkcji \(f(x)\).

\(m=-2\) lub \(m=2\)

Wyznacz wszystkie parametry \(m\) dla których prosta o równaniu \(y = (m - 1)x + 5\) jest

rosnąca
równoległa do prostej \(y = -6x + 3\)

a) \(m\gt 1\)
b) \(m=-5\)

Wyznacz wszystkie parametry \(m\) dla których prosta o równaniu \(y = (3 - 2m)x + 5\) jest

malejąca
prostopadła do prostej \(y = 2x-3\)

a) \(m\gt \frac{3}{2}\)
b) \(m=\frac{7}{4}\)

Rozwiąż równanie \(\frac{4x^2-100}{5+x}=0\).

\(x=5\)

Liczby \(x_1\) oraz \(x_2\) są rozwiązaniami równania \(x^2 - 9 = 0\). Oblicz wartość liczbową wyrażenia \(\frac{x_1+x_2}{2}\).

\(0\)

Liczby \(x_1\) oraz \(x_2\) są rozwiązaniami równania \((x + 1)(2 - x) = 0\). Oblicz \({x_1}^2+x_1x_2+{x_2}^2\).

\(3\)

Dane są punkty \(A = (0,2)\) oraz \(B = (2,1)\). Wyznacz równanie prostej \(AB\).

\(y=-\frac{1}{2}x+2\)

Oblicz medianę oraz średnią arytmetyczną danych: \(1, 2, 4, 7, 1\).

mediana: \(2\), średnia arytmetyczna: \(3\)

Kąt \(\alpha \) jest ostry i \(\cos \alpha =\frac{4}{5}\). Oblicz \(\sin \alpha \) i \(\operatorname{tg} \alpha \).

\(\sin \alpha =\frac{3}{5}\), \(\operatorname{tg} \alpha =\frac{3}{4}\)

Liczby \(x + 1, 2x + 2, 8\) są trzema kolejnymi wyrazami ciągu arytmetycznego. Oblicz \(x\).

\(x=\frac{5}{3}\)

Liczby \(2x, 16, x\) są trzema kolejnymi wyrazami ciągu geometrycznego. Oblicz \(x\).

\(x=8\sqrt{2}\) lub \(x=-8\sqrt{2}\)

Ciąg dany jest wzorem \(a_n=(-1)^n+\frac{n^2+n}{2n-1}\). Oblicz \(a_1\) i \(a_6\).

\(a_1=1\), \(a_6=\frac{53}{11}\)

Podstawy trapezu równoramiennego mają długości \(5\) i \(13\) oraz tangens kąta ostrego jest równy \(2\). Oblicz pole tego trapezu.

\(P=72\)

Adam rozwiązywał codziennie taką sama liczbę zadań i w sumie rozwiązał \(60\) zadań. Jeśli rozwiązywałby codziennie o \(6\) zadań więcej, to rozwiązałby te zadania o \(5\) dni krócej. Oblicz, przez ile dni Adam rozwiązywał zadania przed maturą i ile zadań rozwiązywał każdego dnia.

Przez \(10\) dni rozwiązywał po \(6\) zadań.

W czasie wakacji Marcin przejechał rowerem ze stałą prędkością odległość z miasteczka \(A\) do \(B\) liczącą \(120\) km. Gdyby jechał ze średnią prędkością o \(5\) km/godz. większą, to przejechałby tę odległość w czasie o \(2\) godziny krótszym. Wyznacz średnią rzeczywistą prędkość Marcina i rzeczywisty czas przejazdu.

\(v=15\) km/h, \(t=8\) h

W pojemniku umieszczono \(50\) drewnianych klocków, przy czym każdy klocek ma kształt sześcianu lub kuli, oraz każdy klocek jest czerwony lub niebieski. Wiadomo, że w pojemniku znajduje się dokładnie \(15\) czerwonych sześcianów, \(18\) klocków niebieskich i \(31\) klocków mających kształt kuli. Z pojemnika losowo wybieramy jeden klocek. Oblicz prawdopodobieństwo, że wylosowany klocek jest niebieską kulą?

\(\frac{7}{25}\)

Oblicz kąt \(\alpha \) między cięciwą \(PQ\), a styczną do okręgu w punkcie \(P\).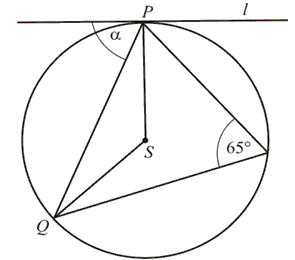

\(\alpha =65^\circ \)

Suma \(n\) początkowych wyrazów pewnego ciągu liczbowego \((a_n)\) wyraża się wzorem \(S_n = 3n^2 + 8n\). Wyznacz dwa początkowe wyrazy ciągu \((a_n)\).

\(a_1=11\), \(a_2=17\)

W urnie jest \(6\) kul oznaczonych kolejnymi cyframi od \(1\) do \(6\). Doświadczenie losowe polega na dwukrotnym losowaniu jednej kuli, przy czym po pierwszym losowaniu kula nie wraca do urny. Cyfra, jaką jest oznaczona pierwsza wylosowana kula, jest cyfrą jedności, a cyfra na drugiej kuli jest cyfrą dziesiątek liczby dwucyfrowej. Oblicz prawdopodobieństwo zdarzenia \(A\) polegającego na tym, że otrzymana liczba jest taką liczbą podzielną przez \(3\), której cyfra jedności jest nie większa niż \(4\).

\(P(A)=\frac{7}{30}\)