W hurtowni owoców wyselekcjonowane jabłko spełnia normę jakości, gdy jego masa (po zaokrągleniu do pełnych dekagramów) mieści się w przedziale [\(19\) dag, \(21\) dag]. Pobrano próbę kontrolną liczącą \(50\) jabłek i następnie zważono każde z nich. Na poniższym wykresie słupkowym przedstawiono rozkład masy jabłek w badanej próbie. Na osi poziomej podano - wyrażoną w dekagramach - masę jabłka (w zaokrągleniu do pełnych dekagramów), a na osi pionowej przedstawiono liczbę jabłek o określonej masie. 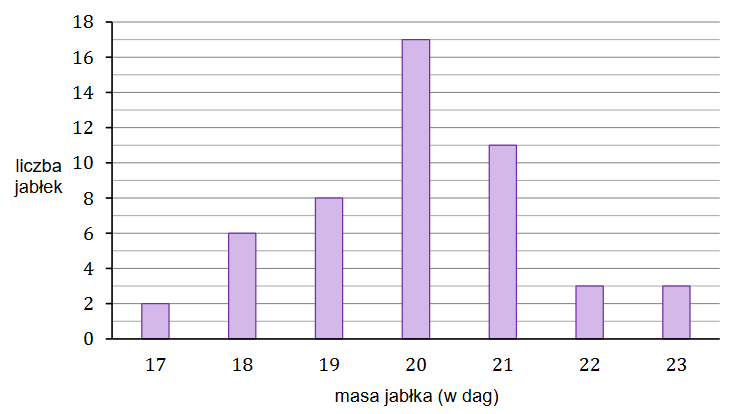

Spośród \(50\) zważonych jabłek z pobranej próby kontrolnej losujemy jedno jabłko.
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Prawdopodobieństwo zdarzenia polegającego na tym, że wylosowane jabłko spełnia normę jakości, jest równe A.\( \frac{3}{7} \)
B.\( \frac{5}{7} \)
C.\( \frac{18}{25} \)
D.\( \frac{9}{10} \)
Dokończ zdanie tak, aby było prawdziwe. Wybierz odpowiedź A albo B oraz jej uzasadnienie 1., 2. albo 3.
Dominanta masy \(50\) zważonych jabłek (w zaokrągleniu do pełnych dekagramów) z pobranej próby kontrolnej jest równa | A. | 20 dag | ponieważ | 1. | ta masa jest największa w tej próbie. |
| 2. | iloczyn tej masy i liczby jabłek o takiej masie jest największy w tej próbie. | |||
| B. | 23 dag | |||
| 3. | ta masa występuje najliczniej w tej próbie. | |||
Strony z tym zadaniem
Matura 2023 grudzieńPewniaki maturalne - formuła 2023Sąsiednie zadania
Zadanie 4066Zadanie 4067Zadanie 4068 (tu jesteś)
Zadanie 4069Zadanie 4070