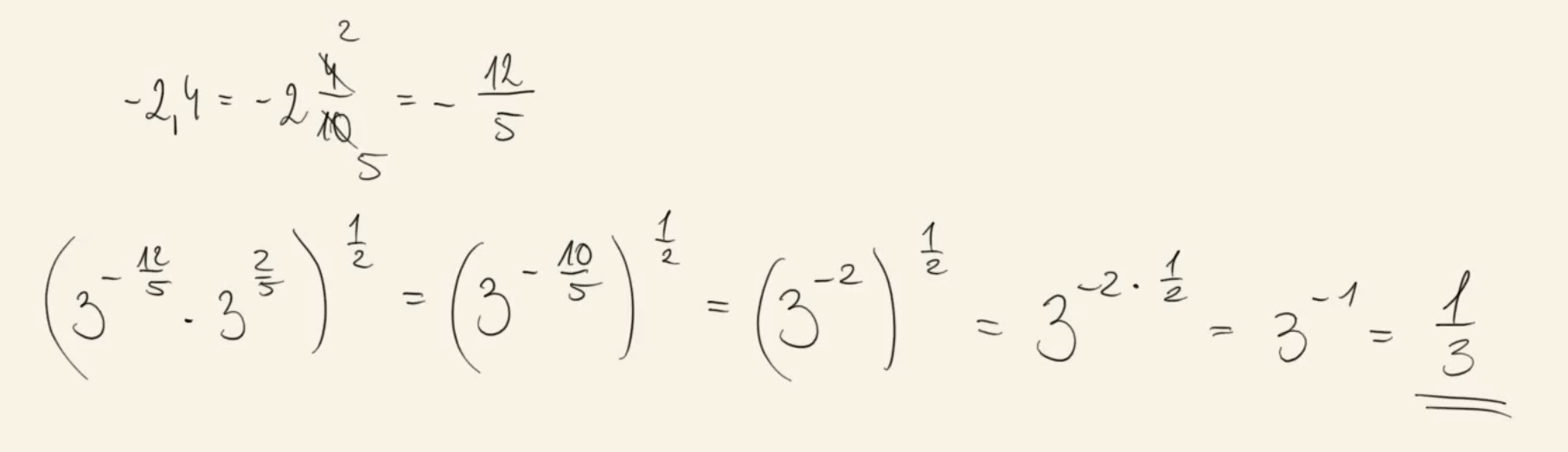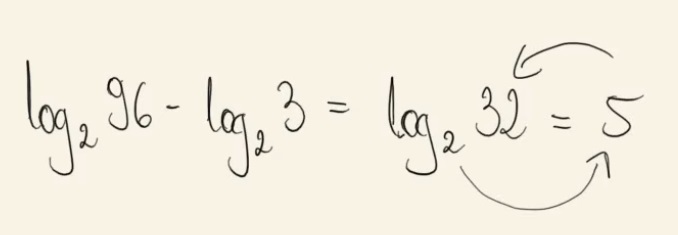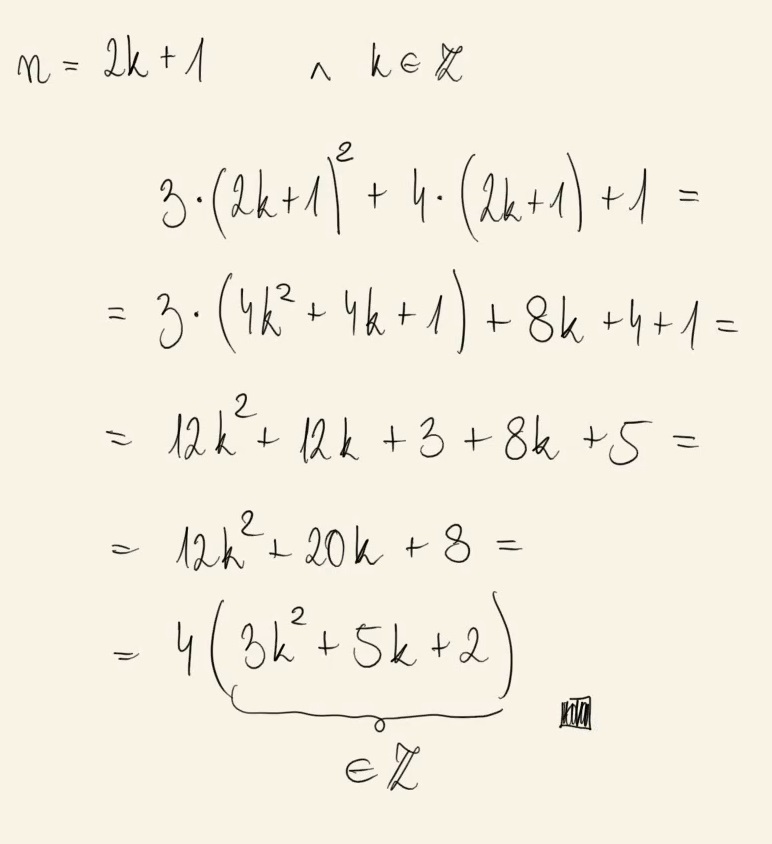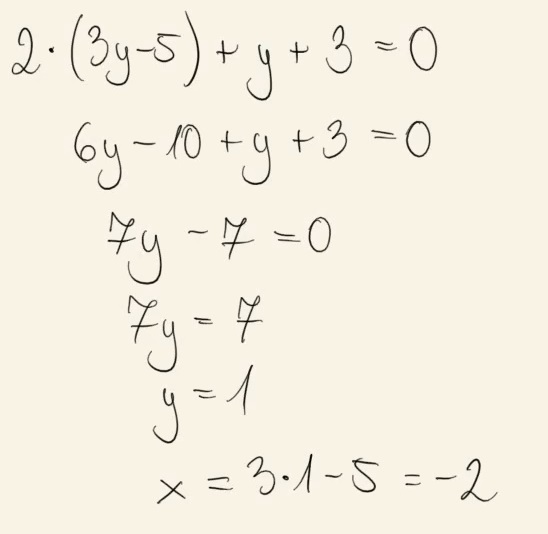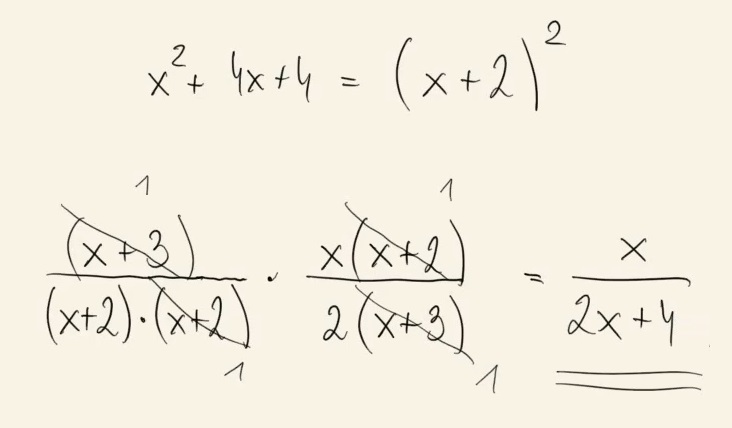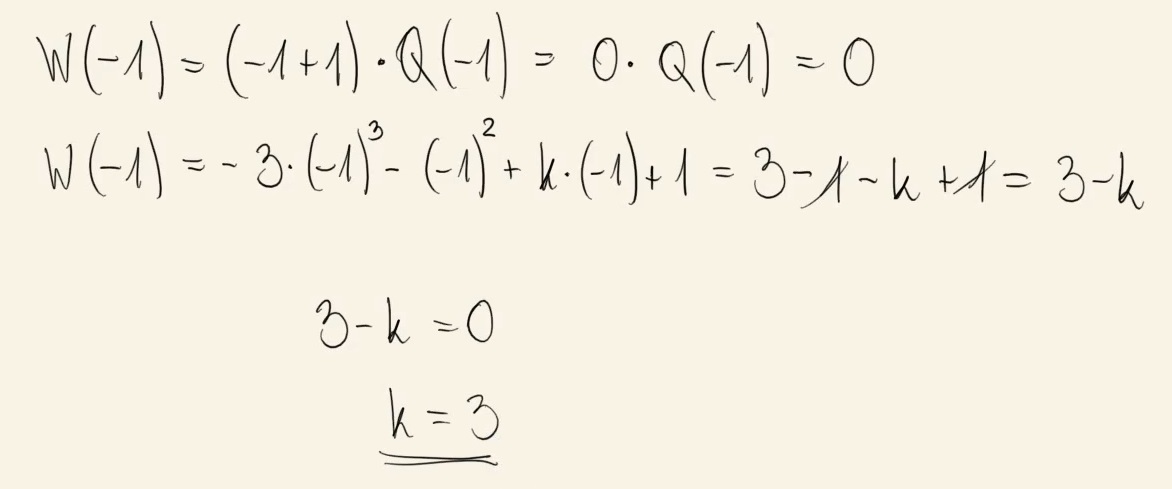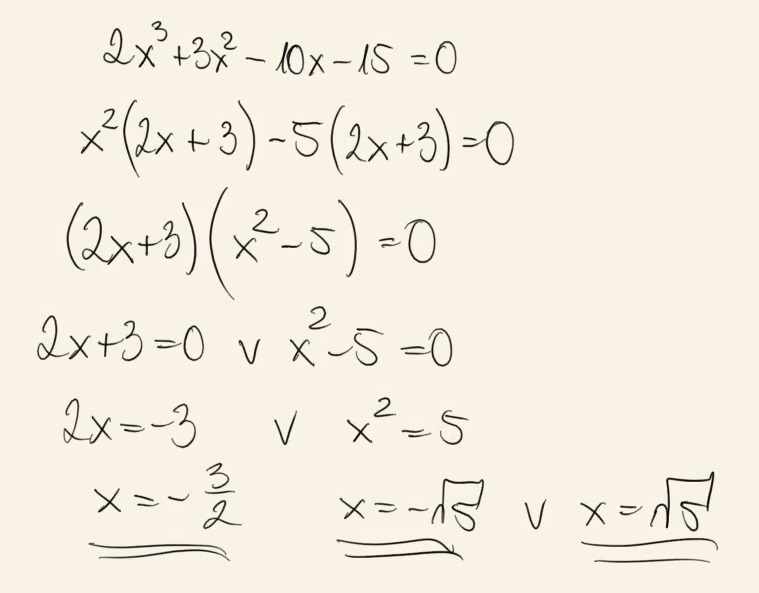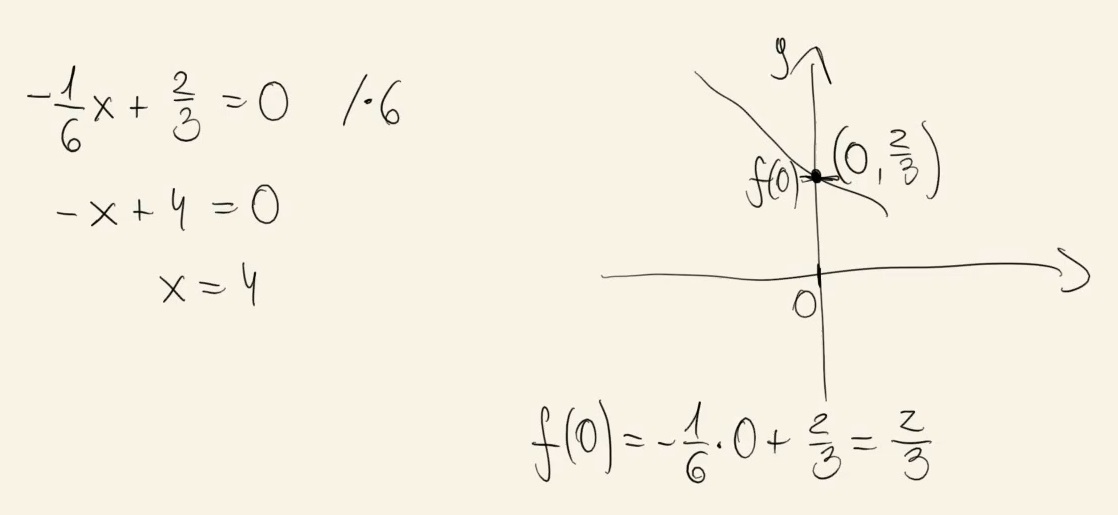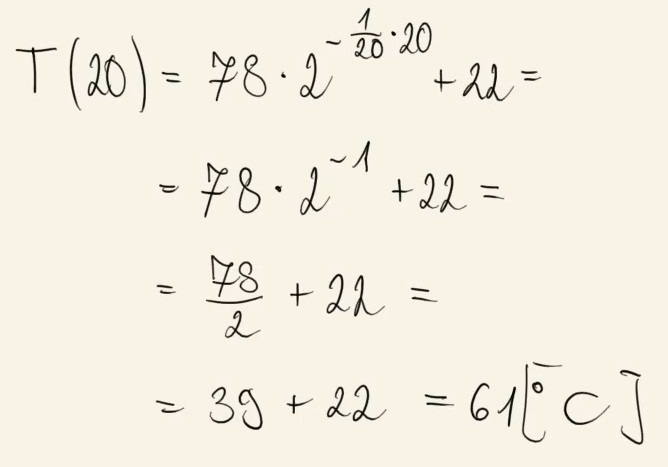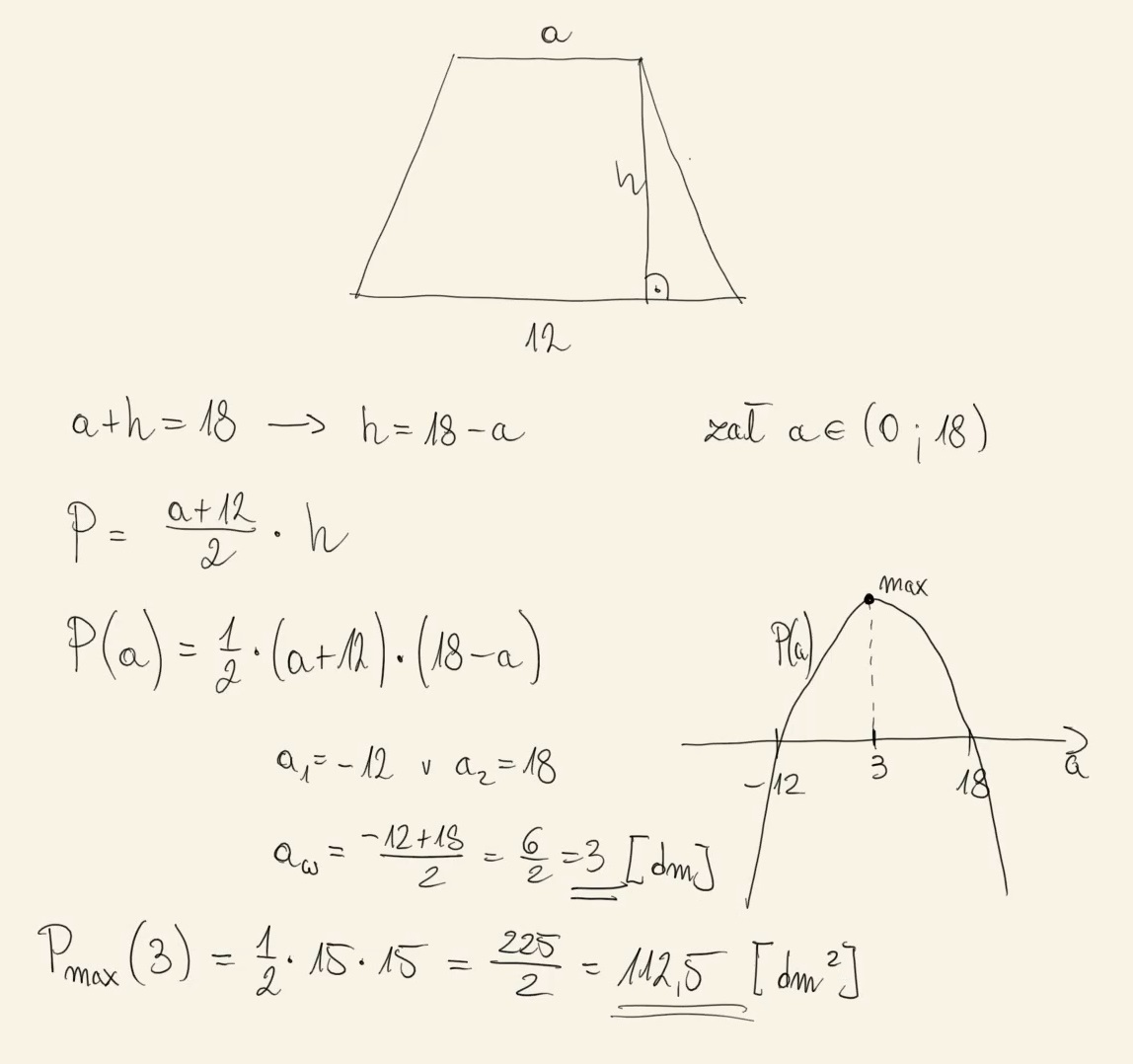Matura podstawowa 2023 - grudzień - próbna CKE
Poziom podstawowy
Pliki do pobrania: Arkusz można też wydrukować w prawym górnym rogu strony według własnych preferencji.
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Liczba \(\left(3^{-2,4}\cdot 3^{\Large{\frac{2}{5}}}\right)^{\Large{\frac{1}{2}}}\) jest równa A.\( \sqrt{3} \)
B.\( \frac{\sqrt{3}}{3} \)
C.\( \frac{1}{3} \)
D.\( 0{,}3 \)
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Liczba \(\log_296-\log_23\) jest równa A.\( \log_293 \)
B.\( \log_230 \)
C.\( 4 \)
D.\( 5 \)
Pan Grzegorz wpłacił do banku pewną kwotę na lokatę dwuletnią.
Po każdym rocznym okresie oszczędzania bank doliczał odsetki w wysokości \(5\%\) od kwoty bieżącego kapitału znajdującego się na lokacie.
Po dwóch latach oszczędzania pan Grzegorz odebrał z tego banku wraz z odsetkami kwotę \(4851\) zł (bez uwzględnienia podatków).
Po każdym rocznym okresie oszczędzania bank doliczał odsetki w wysokości \(5\%\) od kwoty bieżącego kapitału znajdującego się na lokacie.
Po dwóch latach oszczędzania pan Grzegorz odebrał z tego banku wraz z odsetkami kwotę \(4851\) zł (bez uwzględnienia podatków).
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Kwota wpłacona przez pana Grzegorza na tę lokatę była równa A.\( 4300 \) zł
B.\( 4400 \) zł
C.\( 4500 \) zł
D.\( 4600 \) zł
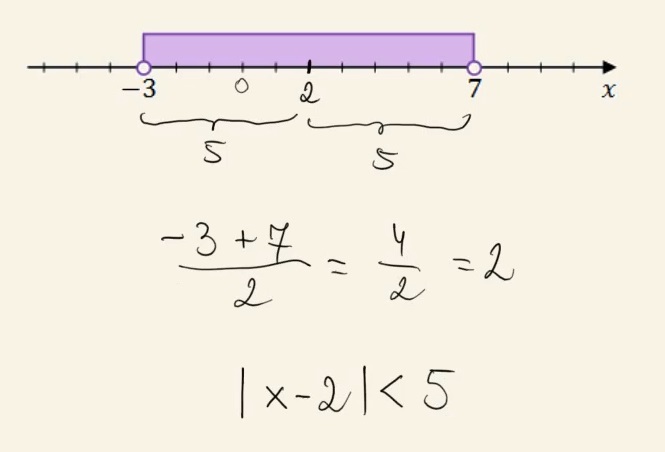
Na osi liczbowej zaznaczono przedział. 

Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Zbiór zaznaczony na osi jest zbiorem wszystkich rozwiązań nierówności A.\( |x-2|\lt 5 \)
B.\( |x-5|\lt 2 \)
C.\( |x-2|\gt 5 \)
D.\( |x-5|\gt 2 \)
Wykaż, że dla każdej liczby całkowitej nieparzystej \(n\) liczba \(3n^2+4n+1\) jest podzielna przez \(4\).
Dany jest układ równań \(\begin{cases} x - 3y + 5 = 0 \\ 2x + y + 3 = 0 \end{cases} \)
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Rozwiązaniem tego układu równań jest para liczb A.\( x=1 \) i \(y=2\)
B.\( x=0 \) i \(y=-3 \)
C.\( x=-2 \) i \(y=1 \)
D.\( x=-1 \) i \(y=-1 \)
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Dla każdej liczby rzeczywistej \(x\) różnej od \((-3)\) i \((-2)\) wartość wyrażenia \(\frac{x+3}{x^2+4x+4}\cdot \frac{x^2+2x}{2x+6}\) jest równa wartości wyrażenia A.\( \frac{x}{2} \)
B.\( \frac{x}{4} \)
C.\( \frac{x}{2x+4} \)
D.\( \frac{x^3+3x^2}{6x^2+24x+24} \)
Dany jest wielomian \(W(x) = -3x^3 - x^2 + kx + 1\), gdzie \(k\) jest pewną liczbą rzeczywistą. Wiadomo, że wielomian \(W\) można zapisać w postaci \(W(x) = (x + 1)\cdot Q(x)\) dla pewnego wielomianu \(Q\).
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Liczba \(k\) jest równa A.\( 29 \)
B.\( (-3) \)
C.\( 0 \)
D.\( 3 \)
Rozwiąż równanie \[2x^3+3x^2=10x+15\] Zapisz obliczenia.
Funkcja liniowa \(f\) jest określona wzorem \(f(x) = -\frac{1}{6}x+\frac{2}{3}\) .
Oceń prawdziwość poniższych stwierdzeń. Wybierz P, jeśli stwierdzenie jest prawdziwe, albo F - jeśli jest fałszywe.
| Miejscem zerowym funkcji \(f\) jest liczba \(4\). | P | F |
| Punkt przecięcia wykresu funkcji \(f\) z osią \(Oy\) ma współrzędne \(\left(0, -\frac{1}{6}\right)\) | P | F |
W kartezjańskim układzie współrzędnych \((x, y)\) przedstawiono fragment wykresu funkcji kwadratowej \(f\) (zobacz rysunek). Wierzchołek paraboli, która jest wykresem funkcji \(f\), oraz punkty przecięcia paraboli z osiami układu współrzędnych mają współrzędne całkowite. 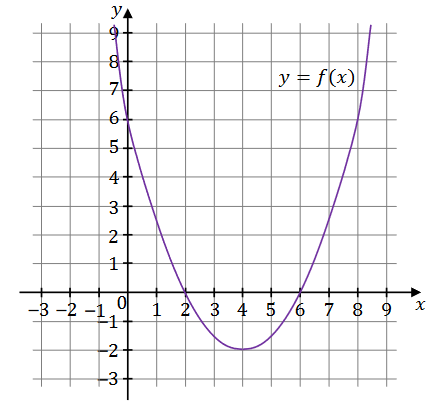

Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Zbiorem wartości funkcji \(f\) jest przedział A.\( (-\infty,-2\rangle \)
B.\( (-\infty,4\rangle \)
C.\( \langle -2,+\infty) \)
D.\( \langle 4,+\infty) \)
Zapisz poniżej w postaci przedziału zbiór wszystkich argumentów, dla których funkcja \(f\) przyjmuje wartości ujemne.
Uzupełnij zdanie. Wybierz dwie właściwe odpowiedzi spośród oznaczonych literami A-F i wpisz te litery w wykropkowanych miejscach.
Wzór funkcji \(f\) można przedstawić w postaci: ………. oraz ………. . A.\( f(x)=\frac{1}{2}(x-2)(x-6) \)
B.\( f(x)=\frac{1}{2}(x-4)^2-2 \)
C.\( f(x)=2(x-2)(x-6) \)
D.\( f(x)=\frac{1}{2}(x+4)^2-2 \)
E.\( f(x)=2(x+2)(x+6) \)
F.\( f(x)=2(x+4)^2-2 \)
Funkcja kwadratowa \(g\) jest określona za pomocą funkcji \(f\) następująco: \(g(x) = f(x + 1)\). Na jednym z rysunków A-D przedstawiono, w kartezjańskim układzie współrzędnych \((x, y)\), fragment wykresu funkcji \(y = g(x)\). 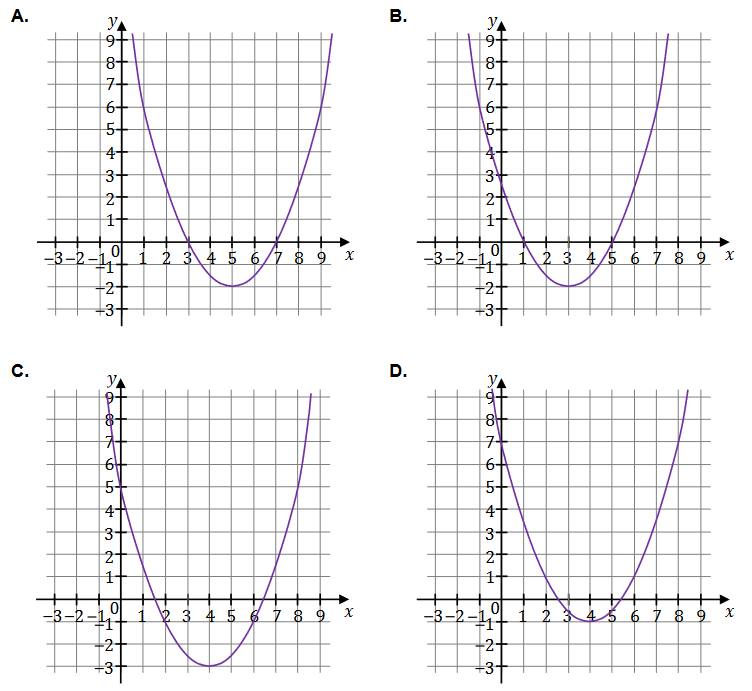
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Fragment wykresu funkcji \(y = g(x)\) przedstawiono na rysunku 
Proces stygnięcia naparu z ziół w otoczeniu o stałej temperaturze \(22^\circ\)C opisuje funkcja wykładnicza \(T(x) = 78\cdot 2^{-0{,}05x}+22\), gdzie \(T(x)\) to temperatura naparu wyrażona w stopniach Celsjusza (\(^\circ\)C) po \(x\) minutach liczonych od momentu \(x = 0\), w którym zioła zalano wrzątkiem.
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Temperatura naparu po \(20\) minutach od momentu zalania ziół wrzątkiem jest równa A.\( 22^\circ\)C
B.\( 39^\circ\)C
C.\( 78^\circ\)C
D.\( 61^\circ\)C
Ciąg arytmetyczny \((a_n)\) jest określony dla każdej liczby naturalnej \(n \ge 1\). W tym ciągu \(a_2 = 4\) oraz \(a_3 = 9\).
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Szósty wyraz ciągu \((a_n)\) jest równy A.\( 24 \)
B.\( 29 \)
C.\( 36 \)
D.\( 69 \)
Ciąg \((a_n)\) jest określony dla każdej liczby naturalnej \(n \ge 1\). Suma \(n\) początkowych wyrazów tego ciągu jest określona wzorem \(S_n = 4\cdot (2^n - 1)\) dla każdej liczby naturalnej \(n \ge 1\).
Oceń prawdziwość poniższych stwierdzeń. Wybierz P, jeśli stwierdzenie jest prawdziwe, albo F - jeśli jest fałszywe.
| Pierwszy wyraz ciągu \((a_n)\) jest równy \(4\). | P | F |
| Drugi wyraz ciągu \((a_n)\) jest równy \(12\). | P | F |
Trzywyrazowy ciąg \((1 - 2a, 12, 48)\) jest geometryczny.
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Liczba \(a\) jest równa A.\( (-1) \)
B.\( 3 \)
C.\( 4 \)
D.\( 12{,}5 \)
Dane są dwa kąty o miarach \(\alpha\) oraz \(\beta\), spełniające warunki:
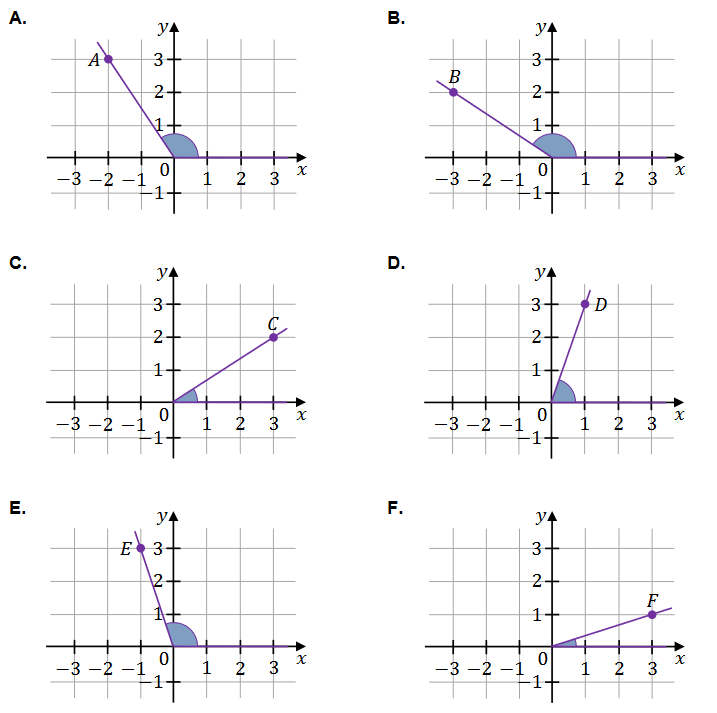
\(\alpha \in (0^\circ, 180^\circ)\) i \(\operatorname{tg} \alpha = -\frac{2}{3}\) oraz \(\beta \in (0^\circ, 180^\circ)\) i \(\cos \beta = \frac{1}{\sqrt{10}}\).
Na rysunkach A-F w kartezjańskim układzie współrzędnych \((x, y)\) zaznaczono różne kąty - w tym kąt o mierze \(\alpha\) oraz kąt o mierze \(\beta\). Jedno z ramion każdego z tych kątów pokrywa się z dodatnią półosią \(Ox\), a drugie przechodzi przez jeden z punktów o współrzędnych całkowitych: \(A\) lub \(B\), lub \(C\), lub \(D\), lub \(E\), lub \(F\).
Uzupełnij tabelę. Wpisz w każdą pustą komórkę tabeli właściwą odpowiedź, wybraną spośród oznaczonych literami A-F.
| 1. | Kąt \(\alpha\) jest zaznaczony na rysunku | |
| 2. | Kąt \(\beta\) jest zaznaczony na rysunku |

Kąt \(\alpha\) jest ostry oraz \(\sin \alpha = \frac{\sqrt{5}}{3}\) .
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Tangens kąta \(\alpha\) jest równy A.\( \frac{\sqrt{5}}{2} \)
B.\( \frac{2}{3} \)
C.\( \frac{2\sqrt{5}}{5} \)
D.\( \frac{3\sqrt{5}}{5} \)
W kartezjańskim układzie współrzędnych \((x, y)\) dana jest prosta \(l\) o równaniu \(y = \frac{3}{2}x-\frac{15}{2}\). Prosta \(k\) jest prostopadła do prostej \(l\) i przechodzi przez punkt \(P = (6, 0)\).
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Prosta \(k\) ma równanie A.\( y=\frac{3}{2}x+6 \)
B.\( y=-\frac{2}{3}x+6 \)
C.\( y=\frac{3}{2}x-9 \)
D.\( y=-\frac{2}{3}x+4 \)
W kartezjańskim układzie współrzędnych \((x, y)\) dane są proste \(k\) oraz \(l\) o równaniach \[k: y=-\frac{1}{2}x-7\] \[l: y=(2m-1)x+13\]
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Proste \(k\) oraz \(l\) są równoległe, gdy A.\( m=-\frac{1}{2} \)
B.\( m=\frac{1}{4} \)
C.\( m=\frac{3}{2} \)
D.\( m=2 \)
W kartezjańskim układzie współrzędnych \((x, y)\) dany jest okrąg \(O\) o środku w punkcie \(S = (4, -2)\). Okrąg \(O\) jest styczny do osi \(Ox\) układu współrzędnych.
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Okrąg \(O\) jest określony równaniem A.\( (x-4)^2+(y+2)^2=4 \)
B.\( (x-4)^2+(y+2)^2=2 \)
C.\( (x+4)^2+(y-2)^2=4 \)
D.\( (x+4)^2+(y-2)^2=2 \)
W kartezjańskim układzie współrzędnych \((x, y)\) punkty \(K = (-7, -2)\) oraz \(L = (-1, 4)\) są wierzchołkami trójkąta równobocznego \(KLM\).
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Pole trójkąta \(KLM\) jest równe A.\( 17\sqrt{2} \)
B.\( 17\sqrt{3} \)
C.\( 18\sqrt{2} \)
D.\( 18\sqrt{3} \)
Punkty \(A\), \(B\) oraz \(C\) leżą na okręgu o środku w punkcie \(O\). Prosta \(k\) jest styczna do tego okręgu w punkcie \(A\) i tworzy z cięciwą \(AB\) kąt o mierze \(32^\circ\). Ponadto odcinek \(AC\) jest średnicą tego okręgu (zobacz rysunek). 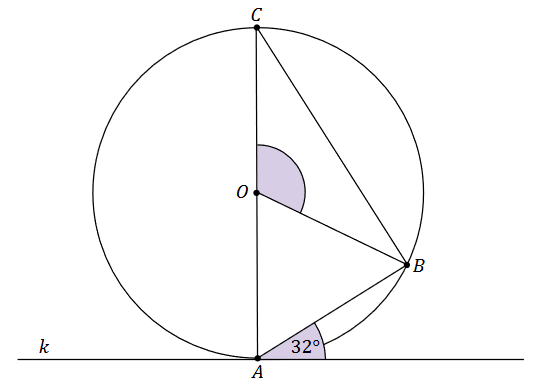

Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Miara kąta rozwartego \(BOC\) jest równa A.\( 148^\circ \)
B.\( 116^\circ \)
C.\( 154^\circ \)
D.\( 122^\circ \)
W rombie \(ABCD\) dłuższa przekątna \(AC\) ma długość \(12\) i tworzy z bokiem \(AB\) kąt o mierze \(30^\circ\) (zobacz rysunek). 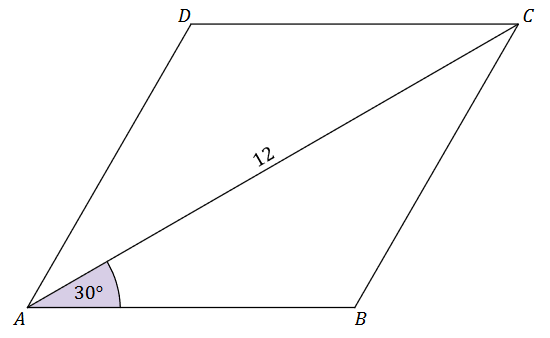

Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Pole rombu \(ABCD\) jest równe A.\( 24 \)
B.\( 36 \)
C.\( 24\sqrt{3} \)
D.\( 36\sqrt{2} \)
Dany jest okrąg \(O\) o środku w punkcie \(S\). Średnica \(AB\) tego okręgu przecina cięciwę \(CD\) w punkcie \(P\) (zobacz rysunek). Ponadto: \(|PB| = 4\), \(|PC| = 8\) oraz \(|PD| = 5\). 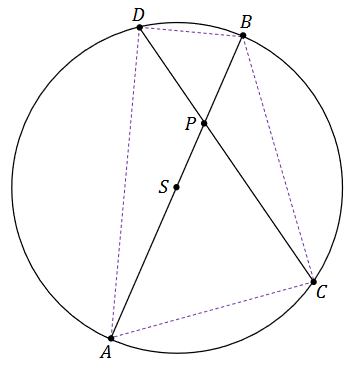

Oblicz promień okręgu \(O\). Zapisz obliczenia.
Dany jest sześcian \(ABCDEFGH\) o krawędzi długości \(5\). Wewnątrz sześcianu znajduje się punkt \(P\) (zobacz rysunek). 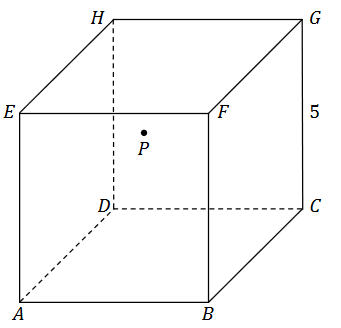

Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Suma odległości punktu \(\)P od wszystkich ścian sześcianu \(ABCDEFGH\) jest równa A.\( 15 \)
B.\( 20 \)
C.\( 25 \)
D.\( 30 \)
Objętość ostrosłupa prawidłowego czworokątnego jest równa \(384\). Wysokość ściany bocznej tego ostrosłupa tworzy z płaszczyzną podstawy kąt o mierze \(\alpha\) taki, że \(\operatorname{tg} \alpha =\frac{4}{3}\) (zobacz rysunek). 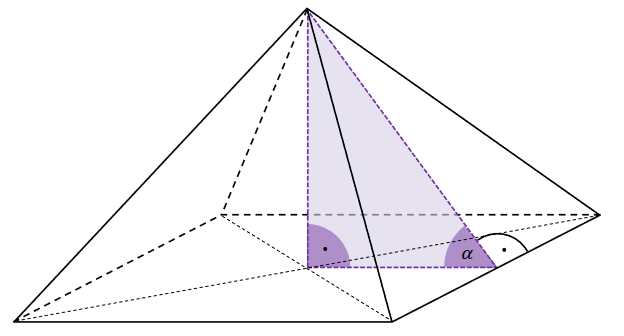

Oblicz wysokość ściany bocznej tego ostrosłupa. Zapisz obliczenia.
E-dowód ma zapisany na pierwszej stronie specjalny sześciocyfrowy numer CAN, który zabezpiecza go przed odczytaniem danych przez osoby nieuprawnione.
Oblicz, ile jest wszystkich sześciocyfrowych numerów CAN o różnych cyfrach, spełniających warunek: trzy pierwsze cyfry są kolejnymi wyrazami ciągu arytmetycznego o różnicy \((-3)\). Zapisz obliczenia.
Doświadczenie losowe polega na dwukrotnym rzucie symetryczną sześcienną kostką do gry, która na każdej ściance ma inną liczbę oczek - od jednego oczka do sześciu oczek.
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Prawdopodobieństwo zdarzenia polegającego na tym, że iloczyn liczb wyrzuconych oczek jest liczbą nieparzystą, jest równe A.\( \frac{1}{2} \)
B.\( \frac{1}{5} \)
C.\( \frac{1}{4} \)
D.\( \frac{3}{4} \)
W hurtowni owoców wyselekcjonowane jabłko spełnia normę jakości, gdy jego masa (po zaokrągleniu do pełnych dekagramów) mieści się w przedziale [\(19\) dag, \(21\) dag]. Pobrano próbę kontrolną liczącą \(50\) jabłek i następnie zważono każde z nich. Na poniższym wykresie słupkowym przedstawiono rozkład masy jabłek w badanej próbie. Na osi poziomej podano - wyrażoną w dekagramach - masę jabłka (w zaokrągleniu do pełnych dekagramów), a na osi pionowej przedstawiono liczbę jabłek o określonej masie. 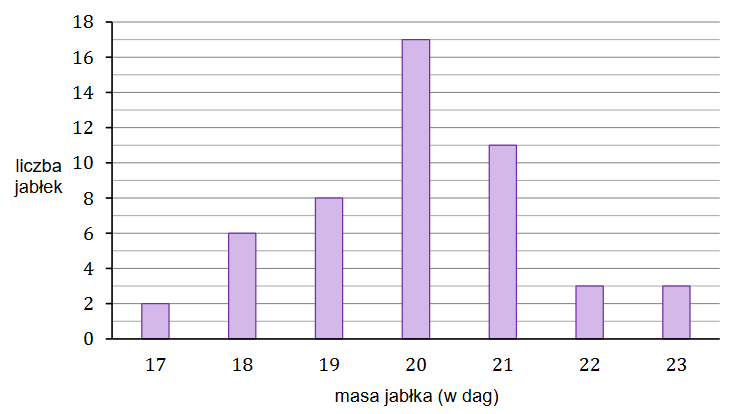

Spośród \(50\) zważonych jabłek z pobranej próby kontrolnej losujemy jedno jabłko.
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Prawdopodobieństwo zdarzenia polegającego na tym, że wylosowane jabłko spełnia normę jakości, jest równe A.\( \frac{3}{7} \)
B.\( \frac{5}{7} \)
C.\( \frac{18}{25} \)
D.\( \frac{9}{10} \)
Dokończ zdanie tak, aby było prawdziwe. Wybierz odpowiedź A albo B oraz jej uzasadnienie 1., 2. albo 3.
Dominanta masy \(50\) zważonych jabłek (w zaokrągleniu do pełnych dekagramów) z pobranej próby kontrolnej jest równa | A. | 20 dag | ponieważ | 1. | ta masa jest największa w tej próbie. |
| 2. | iloczyn tej masy i liczby jabłek o takiej masie jest największy w tej próbie. | |||
| B. | 23 dag | |||
| 3. | ta masa występuje najliczniej w tej próbie. | |||
Zgodnie z założeniem architekta okno na poddaszu ma mieć kształt trapezu równoramiennego, który nie jest równoległobokiem. Dłuższa podstawa trapezu ma mieć długość \(12\) dm, a suma długości krótszej podstawy i wysokości tego trapezu ma być równa \(18\) dm.
Oblicz, jaką długość powinna mieć krótsza podstawa tego trapezu, tak aby pole powierzchni okna było największe. Oblicz to pole. Zapisz obliczenia.
Tematy nadrzędne i sąsiednie