Dana jest kula o promieniu 1. Rozpatrujemy wszystkie stożki opisane na tej kuli, to znaczy takie, których: 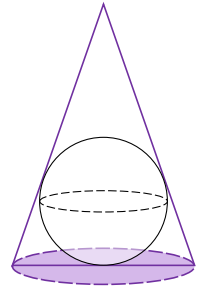podstawa ma dokładnie jeden punkt wspólny z kulą każda tworząca ma dokładnie jeden punkt wspólny z kulą (zobacz rysunek).

Drukuj

Dana jest kula o promieniu \(1\). Rozpatrujemy wszystkie stożki opisane na tej kuli, to znaczy takie, których:

Wykaż, że objętość \(V\) stożka o wysokości \(h\) wyraża się wzorem \[V(h)=\frac{h^2\pi}{3(h-2)}\]

Oblicz wysokość tego stożka, który ma najmniejszą objętość. Oblicz objętość tego stożka. Zapisz obliczenia.

Wskazówka: skorzystaj z informacji, że objętość stożka o wysokości \(h\) wyraża się wzorem \[V(h)=\frac{h^2\pi}{3(h-2)}\]

\(V=\frac{8}{3}\pi\) dla \(h=4\)

Strony z tym zadaniem

Sąsiednie zadania

Zadanie 4011 (tu jesteś)