Matura rozszerzona - zbiór zadań - zadania optymalizacyjne

Drukuj

Poziom rozszerzony

Ciężarówka ma do pokonania trasę długości \(S\) km, poruszając się po autostradzie ze stałą prędkością \(v\) km/h. Minimalna prędkość dla ciężarówek na autostradzie wynosi \(40\) km/h, maksymalna - \(80\) km/h. Wiemy, że litr paliwa kosztuje \(8\) złotych, a kierowca otrzymuje \(42\) złote za godzinę swej pracy. Zużycie paliwa w ciągu jednej godziny jazdy autostradą w zależności od prędkości \(v\) wyrażone w litrach można opisać funkcją \(f(v)=7+\frac{v^2}{400}\).

Oblicz, przy jakiej prędkości koszt przejazdu będzie najmniejszy. Zapisz obliczenia.

Wskazówka: przyjmij, że koszt przejazdu jest sumą kosztu paliwa oraz wynagrodzenia kierowcy.

\(v=70\) km/h

Firma \(X\) wytwarza pewien produkt D. Badania rynku pokazały, że związek między ilością \(Q\) produktu \(D\), jaką firma jest w stanie zbyć na rynku, a ceną \(P\) produktu jest następujący: \[ P(Q)=90-0,1 Q \quad \text { dla } Q \in[0,900] \]

gdzie \(P\) jest ceną za jednostkę produktu w złotych, a \(Q\) - ilością produktu w tys. sztuk.

Koszty \(K\) wytworzenia produktu D zależą od ilości \(Q\) wytwarzanego produktu następująco: \[ K(Q)=0,002 Q^{3}+Q^{2}+29,9985 Q+50 \] gdzie \(K\) jest kosztem produkcji w tys. zł.

Oblicz, przy jakiej wielkości produkcji firma X osiąga największy dochód. Wynik podaj zaokrąglony z dokładnością do 100 sztuk. Zapisz obliczenia.

Dochód firmy jest największy przy wielkości produkcji \(25\ 500\) sztuk.

Rozważamy wszystkie graniastosłupy prawidłowe czworokątne \(ABCDEFGH\), w których odcinek łączący punkt \(O\) przecięcia przekątnych \(AC\) i \(BD\) podstawy \(ABCD\) z dowolnym wierzchołkiem podstawy \(EFGH\) ma długość \(d\) (zobacz rysunek).

Wyznacz zależność objętości \(V\) graniastosłupa od jego wysokości \(h\) i podaj dziedzinę funkcji \(V(h)\).

Wyznacz wysokość tego z rozważanych graniastosłupów, którego objętość jest największa.

Zapisz obliczenia.

\(h=\frac{d}{\sqrt{3}}\)

Grażyna planuje zrobienie pudełka (bez wieczka) w kształcie prostopadłościanu. W tym celu zamierza wykorzystać prostokątny kawałek tektury o wymiarach \(10 \text{ cm} \times 16 \text{ cm}\), odcinając z każdego rogu kwadrat o boku \(x\) cm (zobacz rysunek).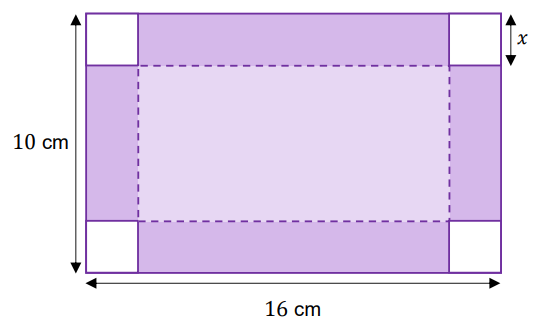

Oblicz wartość \(x\), dla której objętość otrzymanego pudełka będzie największa. Oblicz tę największą objętość pudełka. Zapisz obliczenia.

\(V(2)=144\)

Funkcja \(f\) jest określona wzorem \(f(x)=\frac{12 x-84}{x-8}\) dla każdego \(x \in(-\infty, 8)\). W kartezjańskim układzie współrzędnych \((x, y)\) rozważamy wszystkie czworokąty \(O B C D\), w których: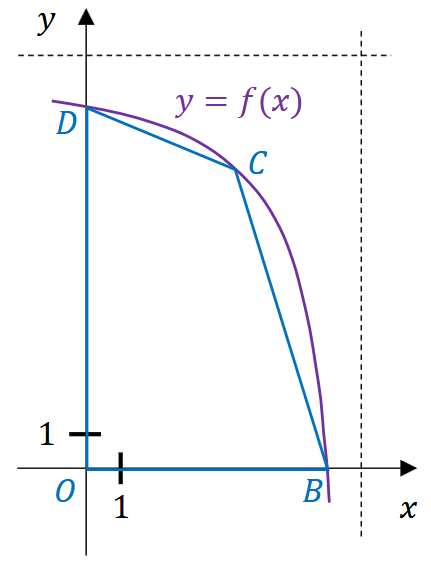

wierzchołek \(O\) ma współrzędne \((0,0)\)
wierzchołki \(B\) oraz \(D\) są punktami przecięcia wykresu funkcji \(f\) z osią odpowiednio - \(Ox\) i \(Oy\)
wierzchołek \(C\) ma obie współrzędne dodatnie i leży na wykresie funkcji \(f\) (zobacz rysunek).

(zobacz rysunek).

Wykaż, że pole \(P\) czworokąta \(OBCD\) w zależności od pierwszej współrzędnej \(x\) punktu \(C\) jest określone wzorem \[ P(x)=\frac{21}{4} \cdot \frac{x^{2}-56}{x-8} \]

Pole \(P\) czworokąta \(OBCD\) w zależności od pierwszej współrzędnej \(x\) punktu \(C\) jest określone wzorem \[ P(x)=\frac{21}{4} \cdot \frac{x^{2}-56}{x-8} \] dla \(x \in(0,7)\).

Oblicz współrzędne wierzchołka \(C\), dla których pole czworokąta \(O B C D\) jest największe. Zapisz obliczenia.

\(C=(8-2\sqrt{2},12-3\sqrt{2})\)

Rozpatrujemy wszystkie trójkąty równoramienne o obwodzie równym \(18\).

Wykaż, że pole \(P\) każdego z tych trójkątów, jako funkcja długości \(b\) ramienia, wyraża się wzorem \(P(b)=\frac{(18-2b)\cdot \sqrt{18b-81}}{2}\)

Wyznacz dziedzinę funkcji \(P\).

Oblicz długości boków tego z rozpatrywanych trójkątów, który ma największe pole.

\(D=\left(\frac{9}{2},9\right)\)
Długości boków: \(6,6,6\).

Pewien zakład otrzymał zamówienie na wykonanie prostopadłościennego zbiornika (całkowicie otwartego od góry) o pojemności \(144 \operatorname{m}^3\). Dno zbiornika ma być kwadratem. Żaden z wymiarów zbiornika (krawędzi prostopadłościanu) nie może przekraczać \(9\) metrów.

Całkowity koszt wykonania zbiornika ustalono w następujący sposób:
– \(100\) zł za \(1 \operatorname{m}^2\) dna
– \(75\) zł za \(1 \operatorname{m}^2\) ściany bocznej.

Oblicz wymiary zbiornika, dla którego tak ustalony koszt wykonania będzie najmniejszy.

\(6, 6, 4\)

Rozpatrujemy wszystkie takie prostopadłościany, w których suma długości wszystkich krawędzi jest równa \(80\), pole powierzchni całkowitej jest równe \(256\) i długości wszystkich krawędzi są nie mniejsze niż \(4\).

Wykaż, że układ równań \[ \begin{align*} 4 a+4 b+4c & =80 \tag{1}\\ 2 ab+2 bc+2ca & =256 \tag{2} \end{align*} \] z niewiadomymi \(a\) oraz \(b\) ma rozwiązanie, które jest parą liczb rzeczywistych nie mniejszych od \(4\) wtedy i tylko wtedy, gdy \(c \in\left[4, \frac{28}{3}\right]\).

Objętość \(V\) każdego z rozpatrywanych prostopadłościanów można wyrazić za pomocą funkcji \[ V(c)=c^{3}-20 c^{2}+128 c \] gdzie \(c \in\left[4, \frac{28}{3}\right]\) jest długością jednej \(z\) krawędzi bryły.

Oblicz objętość tego spośród rozpatrywanych prostopadłościanów, którego objętość jest najmniejsza. Zapisz obliczenia.

Najmniejsza możliwa objętość prostopadłościanu jest równa \(256\). \(V(4)=256, V(8)=256\).

Wśród wszystkich graniastosłupów prawidłowych trójkątnych, w których suma długości wszystkich krawędzi jest równa \(12\), jest taki, który ma największą objętość. Oblicz długości krawędzi tego graniastosłupa i jego objętość.

\(\frac{16\sqrt{3}}{27}\)

Rozważmy wszystkie ostrosłupy prawidłowe sześciokątne, w których suma długości krótszej przekątnej podstawy i wysokości ostrosłupa jest równa \(9\). Wyznacz długość krawędzi podstawy tego z rozważanych ostrosłupów, którego objętość jest największa. Oblicz tę największą objętość.

\(V_{max}(2\sqrt{3})=18\sqrt{3}\)

Parabola o równaniu \(y=2-\frac{1}{2}x^2\) przecina oś \(Ox\) układu współrzędnych w punktach \(A=(-2,0)\) i \(B=(2,0)\). Rozpatrujemy wszystkie trapezy równoramienne \(ABCD\), których dłuższą podstawą jest odcinek \(AB\), a końce \(C\) i \(D\) krótszej podstawy leżą na paraboli (zobacz rysunek). Wyznacz pole trapezu \(ABCD\) w zależności od pierwszej współrzędnej wierzchołka \(C\). Oblicz współrzędne wierzchołka \(C\) tego z rozpatrywanych trapezów, którego pole jest największe.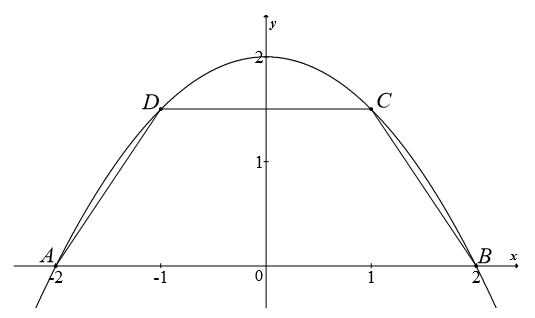

\(P(x)=4-x^2+2x-\frac{1}{2}x^3\)
\(C=\left (\frac{2}{3}, \frac{16}{9} \right )\)

Rozważmy wszystkie graniastosłupy prawidłowe trójkątne o objętości \(V = 2\). Wyznacz długości krawędzi tego z rozważanych graniastosłupów, którego pole powierzchni całkowitej jest najmniejsze. Oblicz to najmniejsze pole.

\(P = 6\sqrt{3}\)

Powierzchnia całkowita graniastosłupa prawidłowego sześciokątnego jest równa \(S\sqrt{3}\). Wyznacz największą z możliwych objętości tego graniastosłupa, wynik zapisz w najprostszej postaci.

\(V_{max}=\frac{S\sqrt{S}}{6}\)

Należy zaprojektować wymiary prostokątnego ekranu smartfona, tak aby odległości tego ekranu od krótszych brzegów smartfona były równe \(0{,}5\) cm każda, a odległości tego ekranu od dłuższych brzegów smartfona były równe \(0{,}3\) cm każda (zobacz rysunek – ekran zaznaczono kolorem szarym). Sam ekran ma mieć powierzchnię \(60\ \text{cm}^2\). Wyznacz takie wymiary ekranu smartfona, przy których powierzchnia ekranu wraz z obramowaniem jest najmniejsza.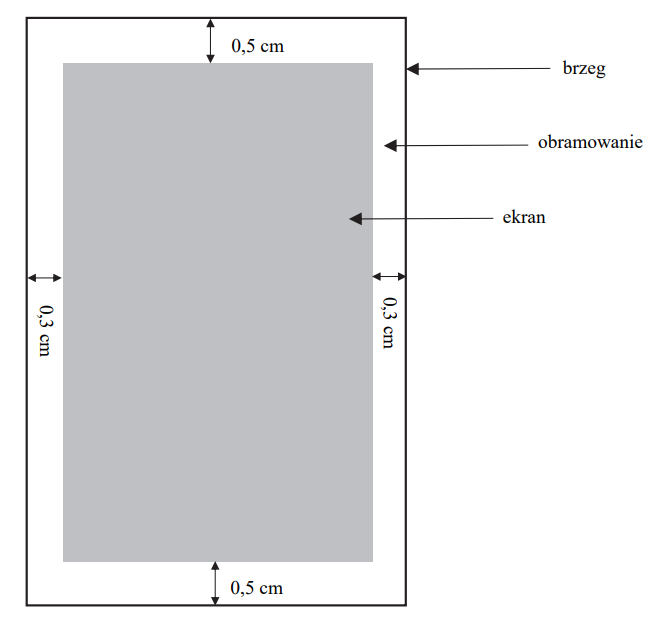

\(6\) i \(10\)

W graniastosłupie prawidłowym trójkątnym suma długości trzech różnych krawędzi wychodzących z jednego wierzchołka wynosi \(S\). Wyznacz objętość tego graniastosłupa jako funkcję długości jednej z jego krawędzi i podaj dziedzinę tej funkcji. Oblicz wymiary graniastosłupa, którego objętość jest największa. Oblicz tę objętość.

\(a=H=\frac{S}{3}, V=\frac{\sqrt{3}}{108}S^3\)

Rozpatrujemy wszystkie trapezy równoramienne, w które można wpisać okrąg, spełniające warunek: suma długości dłuższej podstawy \(a\) i wysokości trapezu jest równa \(2\).

Wyznacz wszystkie wartości \(a\), dla których istnieje trapez o podanych własnościach.

Wykaż, że obwód \(L\) takiego trapezu, jako funkcja długości \(a\) dłuższej podstawy trapezu, wyraża się wzorem \(L(a) = \frac{4a^2 - 8a + 8}{a}\).

Oblicz tangens kąta ostrego tego spośród rozpatrywanych trapezów, którego obwód jest najmniejszy.

a) \(a \in (1, 2)\)
c) \(\operatorname{tg} \alpha = 1\)

Dana jest kula o promieniu \(1\). Rozpatrujemy wszystkie stożki opisane na tej kuli, to znaczy takie, których: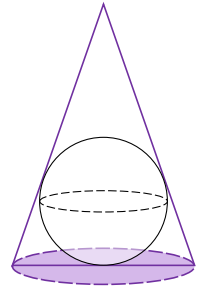

podstawa ma dokładnie jeden punkt wspólny z kulą
każda tworząca ma dokładnie jeden punkt wspólny z kulą (zobacz rysunek).

Wykaż, że objętość \(V\) stożka o wysokości \(h\) wyraża się wzorem \[V(h)=\frac{h^2\pi}{3(h-2)}\]

Oblicz wysokość tego stożka, który ma najmniejszą objętość. Oblicz objętość tego stożka. Zapisz obliczenia.

Wskazówka: skorzystaj z informacji, że objętość stożka o wysokości \(h\) wyraża się wzorem \[V(h)=\frac{h^2\pi}{3(h-2)}\]

\(V=\frac{8}{3}\pi\) dla \(h=4\)

Dana jest kula o promieniu \(1\). Rozpatrujemy wszystkie stożki zawierające środek kuli i wpisane w tę kulę, to znaczy takie, w których: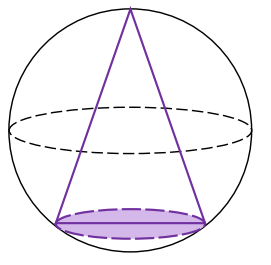

wierzchołek leży na powierzchni kuli
okrąg, będący krawędzią podstawy stożka, leży na powierzchni kuli (zobacz rysunek).

Oblicz promień podstawy tego stożka, który ma największą objętość. Oblicz objętość tego stożka. Zapisz obliczenia.

\(V\left(\frac{2\sqrt{2}}{3}\right)=\frac{32}{81}\pi\)

Na rysunku obok przedstawiono położenie miejscowości \(A, B\) i \(C\) oraz zaznaczono odległości między nimi. O godzinie 9:00 z miejscowości \(A\) do \(C\) wyruszył zastęp harcerzy „Tropiciele" i przemieszczał się z prędkością \(4 \mathrm{~km} / \mathrm{h}\). O tej samej godzinie z miejscowości \(B\) do \(A\) wyruszył zastęp harcerzy „Korsarze" i przemieszczał się z prędkością \(2 \mathrm{~km} / \mathrm{h}\).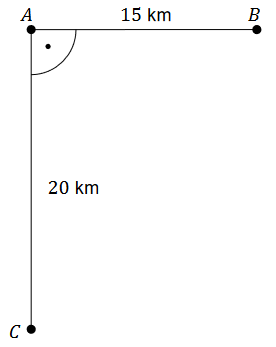

Wyznacz godzinę, o której odległość między tymi zastępami harcerzy będzie najmniejsza. Zapisz obliczenia.

Odległość między zastępami harcerzy będzie najmniejsza o godzinie 10:30.

Syzyf codziennie stoi przed zadaniem wtoczenia ciężkiej kamiennej kuli na szczyt pewnej góry.

W chwili \(t=0\) znajduje się on w punkcie \(\mathcal{O}\) oddalonym od szczytu o \(4\) km, a położenie \(x\) Syzyfa wtaczającego kulę jest opisane zależnością \[x(t)=-t^{3}+16,5 t^{2}+180 t\quad \text{dla}\quad t \in[0,24]\] gdzie \(x\) jest wyrażone w metrach, a \(t\)-w godzinach.
Oś \(\mathcal{O} x\) jest skierowana do wierzchołka góry i jest styczna w każdym punkcie do zbocza góry.

Oblicz najmniejszą odległość, na jaką Syzyf zbliży się do wierzchołka góry, oraz największą prędkość, z jaką wtacza kamień pod górę. Zapisz obliczenia.

Najmniejsza odległość, na jaką Syzyf zbliży się do wierzchołka góry, jest równa \(4000-3037,5=962,5\) metrów.
Największa wartość prędkości, z jaką Syzyf wtacza kulę pod górę, jest równa \(v(5,5)=270,75 \mathrm{~m} / \mathrm{h}\).

Cztery miasta \(A, B, C\) i \(D\) znajdują się w wierzchołkach kwadratu o boku 300 km. Pewna firma dostała zlecenie na zaprojektowanie sieci dróg, która będzie łączyć każde dwa z tych miast. Sieć ma posiadać dwa węzły, a łączna długość dróg w sieci ma być możliwie najmniejsza. (Przykład sieci dróg z dwoma węzłami, łączącej każde dwa z miast, przedstawiono na poniższym rysunku).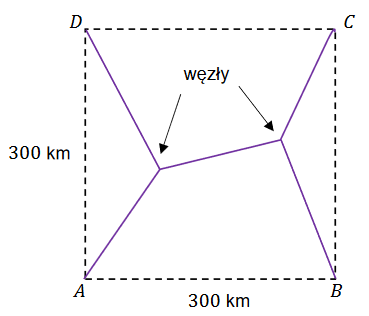

Oblicz, jaka musi być długość najkrótszej takiej sieci dróg i gdzie muszą być zlokalizowane węzły tej sieci. Zapisz obliczenia.

Najkrótsza sieć dróg ma zatem długość \(300(1+\sqrt{3}) \mathrm{km}\).
Jeden węzeł jest równo oddalony (w odległości \(100 \sqrt{3} \mathrm{~km}\) ) od miast \(A\) i \(D\), natomiast drugi węzeł jest równo oddalony (w odległości \(100 \sqrt{3} \mathrm{~km}\) ) od miast \(B\) i \(C\)