Dana jest kula o promieniu \(1\). Rozpatrujemy wszystkie stożki zawierające środek kuli i wpisane w tę kulę, to znaczy takie, w których: 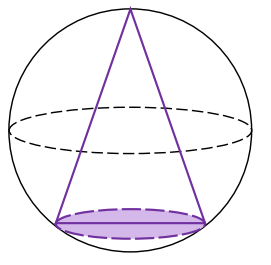
- wierzchołek leży na powierzchni kuli
- okrąg, będący krawędzią podstawy stożka, leży na powierzchni kuli (zobacz rysunek).

Oblicz promień podstawy tego stożka, który ma największą objętość. Oblicz objętość tego stożka. Zapisz obliczenia.
Strony z tym zadaniem
Zadania maturalne CKE - poziom rozszerzonySąsiednie zadania
Zadanie 4008Zadanie 4009Zadanie 4010 (tu jesteś)
Zadanie 4015Zadanie 4016