Sześcian

Drukuj

Poziom podstawowy

Sześcian jest szczególnym przypadkiem prostopadłościanu, w którym wszystkie ściany są w kształcie identycznych kwadratów.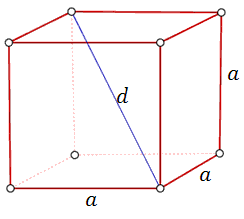

Wzór na pole powierzchni sześcianu: \[P_c = 6a^2\] Wzór na objętość sześcianu: \[V = a^3\] Długość przekątnej sześcianu: \[d=a\sqrt{3}\] Promień kuli wpisanej w sześcian: \[r=\frac{1}{2}a\] Promień kuli opisanej na sześcianie: \[R=\frac{1}{2}d=\frac{1}{2}a\sqrt{3}\]

Objętość sześcianu jest równa \(27\) cm³. Jaka jest suma długości wszystkich krawędzi tego sześcianu?

A.\( 18 \) cm

B.\( 36 \) cm

C.\( 24 \) cm

D.\( 12 \) cm

Objętość sześcianu, w którym przekątna ściany bocznej ma długość \(\frac{\sqrt{2}}{4}\), jest równa

A.\( \frac{1}{64} \)

B.\( \frac{1}{16} \)

C.\( 16 \)

D.\( 64 \)

Suma długości krawędzi sześcianu wynosi \(24\) cm. Pole powierzchni całkowitej tego sześcianu jest równe:

A.\( 32 \) cm²

B.\( 24 \) cm²

C.\( 16 \) cm²

D.\( 8 \) cm²

Objętość sześcianu jest równa \(64\). Pole powierzchni całkowitej tego sześcianu jest równe

A.\( 512 \)

B.\( 384 \)

C.\( 96 \)

D.\( 16 \)

Objętość sześcianu jest równa \(27\). Pole powierzchni całkowitej tego sześcianu jest równe

A.\( 54 \)

B.\( 18 \)

C.\( 12\sqrt{3} \)

D.\( 24\sqrt{3} \)

Pole powierzchni jednej ściany sześcianu jest równe \( 4 \). Objętość tego sześcianu jest równa

A.\(6 \)

B.\(8 \)

C.\(24 \)

D.\(64 \)

Suma długości wszystkich krawędzi sześcianu jest równa \(24\). Objętość tego sześcianu jest równa

A.\( 64 \)

B.\( 27 \)

C.\( 24 \)

D.\( 8 \)

Objętość sześcianu jest równa \(27\). Długość przekątnej tego sześcianu jest równa

A.\( 2\sqrt{2} \)

B.\( 3\sqrt{2} \)

C.\( 2\sqrt{3} \)

D.\( 3\sqrt{3} \)

Dany jest sześcian \(ABCDEFGH\). Siatką ostrosłupa czworokątnego \(ABCDE\) jest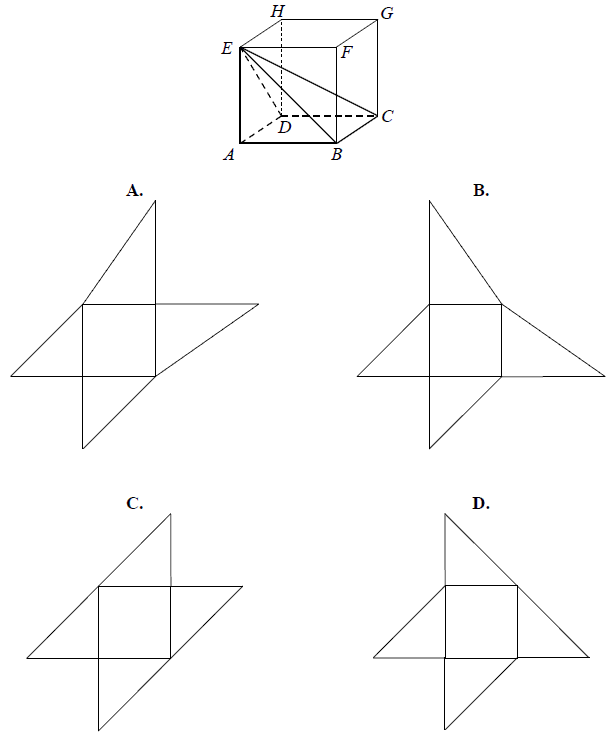

Krawędź sześcianu ma długość \(9\). Długość przekątnej tego sześcianu jest równa

A.\( \sqrt[3]{9} \)

B.\( 9\sqrt{2} \)

C.\( 9\sqrt{3} \)

D.\( 9+9\sqrt{2} \)

Przekątna sześcianu ma długość \(3\). Pole powierzchni całkowitej tego sześcianu jest równe

A.\( 54 \)

B.\( 36 \)

C.\( 18 \)

D.\( 12 \)

Pole powierzchni całkowitej sześcianu jest równe \(24\) cm². Objętość tego sześcianu jest równa

A.\( 8 \) cm³

B.\( 16 \) cm³

C.\( 27 \) cm³

D.\( 64 \) cm³

Dany jest sześcian o przekątnej długości \(4\sqrt{3}\). Objętość tego sześcianu wynosi

A.\( 16 \)

B.\( 16\sqrt{3} \)

C.\( 64 \)

D.\( 64\sqrt{3} \)

Pole powierzchni całkowitej sześcianu jest równe \(54\). Długość przekątnej tego sześcianu jest równa

A.\( \sqrt{6} \)

B.\( 3 \)

C.\( 9 \)

D.\( 3\sqrt{3} \)

Długość krawędzi sześcianu zwiększono o \(20\%\). Oblicz, o ile procent wzrosła objętość tego sześcianu.

\(72{,}8\%\)

Przekątna sześcianu ma długość \(9\). Oblicz pole powierzchni całkowitej tego sześcianu.

\(162\)

Oblicz sinus kąta między przekątną sześcianu, a jego płaszczyzną podstawy.

\(\frac{\sqrt{3}}{3}\)

Punkty \(K\), \(L\) i \(M\) są środkami krawędzi \(BC\), \(GH\) i \(AE\) sześcianu \(ABCDEFGH\) o krawędzi długości \(1\) (zobacz rysunek). Oblicz pole trójkąta \(KLM\).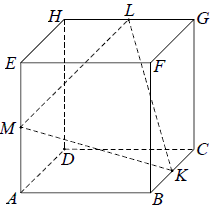

\(\frac{3\sqrt{3}}{8}\)

Krawędź sześcianu jest o \(4\) krótsza od jego przekątnej. Oblicz pole powierzchni całkowitej tego sześcianu.

\(P_c=96+48\sqrt{3}\)

Długość krawędzi sześcianu jest o \(2\) krótsza od długości jego przekątnej. Oblicz długość przekątnej tego sześcianu.

\(3+\sqrt{3}\)

Przekątna ściany sześcianu ma długość \( 5\sqrt{2} \). Pole powierzchni tego sześcianu jest równe:

A.\(5 \)

B.\(25 \)

C.\(150 \)

D.\(125 \)

Pole powierzchni całkowitej sześcianu jest równe \(12\). Suma długości wszystkich krawędzi tego sześcianu jest równa

A.\( 12\sqrt{2} \)

B.\( 8\sqrt{2} \)

C.\( 6\sqrt{2} \)

D.\( 3\sqrt{2} \)

Sześcian o krawędzi \(6\) przecięto płaszczyzną zawierającą przekątną dolnej podstawy i jeden wierzchołek drugiej (patrz rysunek). Oblicz pole otrzymanego przekroju.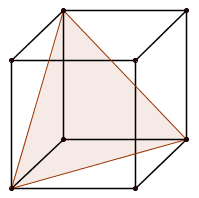

\(P=18\sqrt{3}\)

Przekątna ściany sześcianu ma długość \(2\). Pole powierzchni całkowitej tego sześcianu jest równe

A.\( 24 \)

B.\( 12\sqrt{2} \)

C.\( 12 \)

D.\( 16\sqrt{2} \)