Różne zadania z graniastosłupów
Poziom podstawowy
Liczba wszystkich krawędzi graniastosłupa jest o \(10\) większa od liczby wszystkich jego ścian bocznych. Stąd wynika, że podstawą tego graniastosłupa jest
A.czworokąt
B.pięciokąt
C.sześciokąt
D.dziesięciokąt
Objętość graniastosłupa prawidłowego trójkątnego o wysokości \(7\) jest równa \(28\sqrt{3}\) . Długość krawędzi podstawy tego graniastosłupa jest równa
A.\( 2 \)
B.\( 4 \)
C.\( 8 \)
D.\( 16 \)
Graniastosłup ma \(15\) krawędzi. Ile wierzchołków ma ten graniastosłup?
A.\( 10 \)
B.\( 5 \)
C.\( 15 \)
D.\( 30 \)
Wysokość graniastosłupa prawidłowego czworokątnego jest równa \(6\), a kąt nachylenia jego przekątnej do płaszczyzny podstawy jest równy \(60^\circ \). Długość tej przekątnej jest równa
A.\(3\)
B.\(\sqrt{3}\)
C.\(2\sqrt{3}\)
D.\(4\sqrt{3}\)
W graniastosłupie prawidłowym trójkątnym wszystkie krawędzie są tej samej długości. Suma długości wszystkich krawędzi jest równa \(90\). Wtedy pole powierzchni całkowitej tego graniastosłupa jest równe
A.\( 300 \)
B.\( 300\sqrt{3} \)
C.\( 300+50\sqrt{3} \)
D.\( 300+25\sqrt{3} \)
Graniastosłup ma \(2n+6\) wierzchołków. Liczba wszystkich krawędzi tego graniastosłupa jest równa
A.\( n+3 \)
B.\( 4n+8 \)
C.\( 6n+18 \)
D.\( 3n+9 \)
Dany jest graniastosłup prawidłowy trójkątny \(ABCDEF\) o podstawach \(ABC\) i \(DEF\) i krawędziach bocznych \(AD\), \(BE\) i \(CF\). Oblicz pole trójkąta \(ABF\) wiedząc, że \(|AB|=10\) i \(|CF|= 11\). Narysuj ten graniastosłup i zaznacz na nim trójkąt \(ABF\).
Dany jest graniastosłup prawidłowy trójkątny \(ABCDEF\) o podstawach \(ABC\) i \(DEF\) i krawędziach bocznych \(AD, BE\) i \(CF\) (zobacz rysunek). Długość krawędzi podstawy \(AB\) jest równa \(8\), a pole trójkąta \(ABF\) jest równe \(52\). Oblicz objętość tego graniastosłupa. 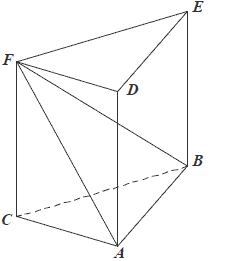

W graniastosłupie prawidłowym czworokątnym \(ABCDEFGH\) przekątna \(AC\) podstawy ma długość \(4\). Kąt \(ACE\) jest równy \(60^\circ\). Oblicz objętość ostrosłupa \(ABCDE\) przedstawionego na poniższym rysunku. 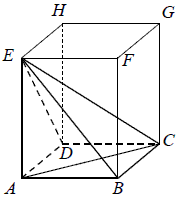

Przekątna graniastosłupa prawidłowego czworokątnego \(ABCDA_1B_1C_1D_1\) ma długość \(2\sqrt{219}\), a krawędź podstawy - \(10\sqrt{2}\). 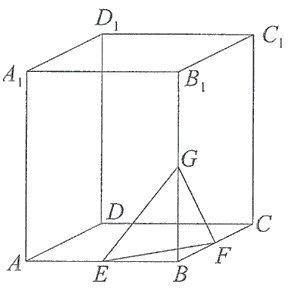 Wyznacz:
Wyznacz:
 Wyznacz:
Wyznacz:- Wysokość graniastosłupa.
- Pole trójkąta \(EFG\), którego wierzchołkami są środki trzech krawędzi wychodzących z jednego wierzchołka podstawy.
Liczba wszystkich krawędzi graniastosłupa jest równa \(24\). Wtedy liczba wszystkich jego wierzchołków jest równa
A.\( 6 \)
B.\( 8 \)
C.\( 12 \)
D.\( 16 \)
W graniastosłupie prawidłowym czworokątnym wysokość graniastosłupa jest o \(4\) krótsza od przekątnej podstawy i o \(8\) krótsza od przekątnej graniastosłupa. Oblicz sinus kąta pomiędzy przekątną graniastosłupa a płaszczyzną podstawy.
W graniastosłupie prawidłowym czworokątnym \( ABCDEFGH \) połączono punkty będące środkami krawędzi \( BC \), \( CD \), \( AD \) i \( GH \). Wyznacz objętość powstałej bryły wiedząc, że \( \vert{DB}\vert=5\sqrt{2} \) i kąt \( DBH \) ma miarę \( 60^\circ \).
Graniastosłup ma \( 10 \) ścian. Liczba wszystkich krawędzi tego graniastosłupa wynosi:
A.\(8 \)
B.\(16 \)
C.\(24 \)
D.\(32 \)
Podstawą graniastosłupa \(ABCDEFGH\) jest prostokąt \(ABCD\) (zobacz rysunek), którego krótszy bok ma długość \(3\). Przekątna prostokąta \(ABCD\) tworzy z jego dłuższym bokiem kąt \(30^\circ\). Przekątna \(HB\) graniastosłupa tworzy z płaszczyzną jego podstawy kąt \(60^\circ\). Oblicz objętość tego graniastosłupa. 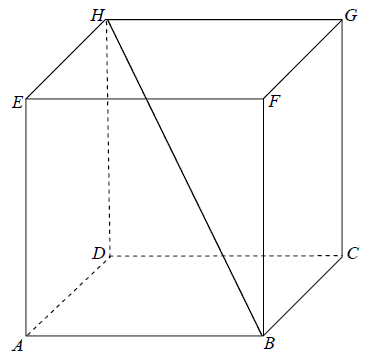

Jacek bawi się sześciennymi klockami o krawędzi \(2\) cm. Zbudował z nich jeden duży sześcian o krawędzi \(8\) cm i wykorzystał do tego wszystkie swoje klocki. Następnie zburzył budowlę i ułożył z tych klocków drugą bryłę – graniastosłup prawidłowy czworokątny. Wtedy okazało się, że został mu dokładnie jeden klocek, którego nie było gdzie dołożyć. Oblicz stosunek pola powierzchni całkowitej pierwszej ułożonej bryły do pola powierzchni całkowitej drugiej bryły i wynik podaj w postaci ułamka nieskracalnego.
Odcinek łączący środki dwóch skośnych krawędzi podstaw graniastosłupa prawidłowego czworokątnego ma długość \(10\). Jaką wysokość powinien mieć ten graniastosłup, aby pole jego powierzchni bocznej było maksymalne?
W graniastosłupie prawidłowym czworokątnym \(EFGHIJKL\) wierzchołki \(E, G, L\) połączono odcinkami (tak jak na rysunku). 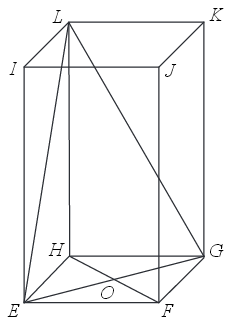 Wskaż kąt między wysokością \(OL\) trójkąta \(EGL\) i płaszczyzną podstawy tego graniastosłupa.
Wskaż kąt między wysokością \(OL\) trójkąta \(EGL\) i płaszczyzną podstawy tego graniastosłupa.
 Wskaż kąt między wysokością \(OL\) trójkąta \(EGL\) i płaszczyzną podstawy tego graniastosłupa.
Wskaż kąt między wysokością \(OL\) trójkąta \(EGL\) i płaszczyzną podstawy tego graniastosłupa. A.\( \sphericalangle OGL \)
B.\( \sphericalangle HOL \)
C.\( \sphericalangle HLO \)
D.\( \sphericalangle OHL \)
Każda krawędź graniastosłupa prawidłowego trójkątnego ma długość równą \(8\). Pole powierzchni całkowitej tego graniastosłupa jest równe
A.\( 8^2\left ( \frac{\sqrt{3}}{2}+3 \right ) \)
B.\( \frac{8^2\sqrt{6}}{3} \)
C.\( 8^2\cdot \sqrt{3} \)
D.\( \frac{8^2}{3}\left ( \frac{\sqrt{3}}{2}+3 \right ) \)
Wysokość graniastosłupa prawidłowego czworokątnego jest równa \(16\). Przekątna graniastosłupa jest nachylona do płaszczyzny podstawy pod kątem, którego cosinus jest równy \(\frac{3}{5}\). Oblicz pole powierzchni całkowitej tego graniastosłupa.
Pole podstawy graniastosłupa prawidłowego czworokątnego jest równe \(36\), a miara kąta nachylenia przekątnej graniastosłupa do płaszczyzny jego podstawy jest równa \(30^\circ\). Wysokość tego graniastosłupa jest równa
A.\( 3\sqrt{2} \)
B.\( 6\sqrt{2} \)
C.\( 2\sqrt{6} \)
D.\( 3\sqrt{6} \)
Pole powierzchni całkowitej graniastosłupa prawidłowego sześciokątnego jest równe \(63 \sqrt{3}\). Krótsza przekątna tego graniastosłupa tworzy z płaszczyzna podstawy kąt \(\alpha\) taki, że \(\operatorname{tg} \alpha=3\). Oblicz długość krawędzi podstawy tego graniastosłupa.
Krawędź podstawy \(ABCD\) graniastosłupa prawidłowego czworokątnego \(A B C D A^{\prime} B^{\prime} C^{\prime} D^{\prime}\) jest równa \(12\). Na krawędzi bocznej \(\mathrm{DD}^{\prime}\) obrano punkt \(P\) taki, że \(|PD^{\prime}|=13\). Graniastosłup ten przecięto płaszczyzna zawierająca przekątna \(AC\) podstawy i przechodząca przez punkt P. Pole tego przekroju jest równe \(54 \sqrt{2}\). Oblicz wysokość tego graniastosłupa.
Tematy nadrzędne i sąsiednie
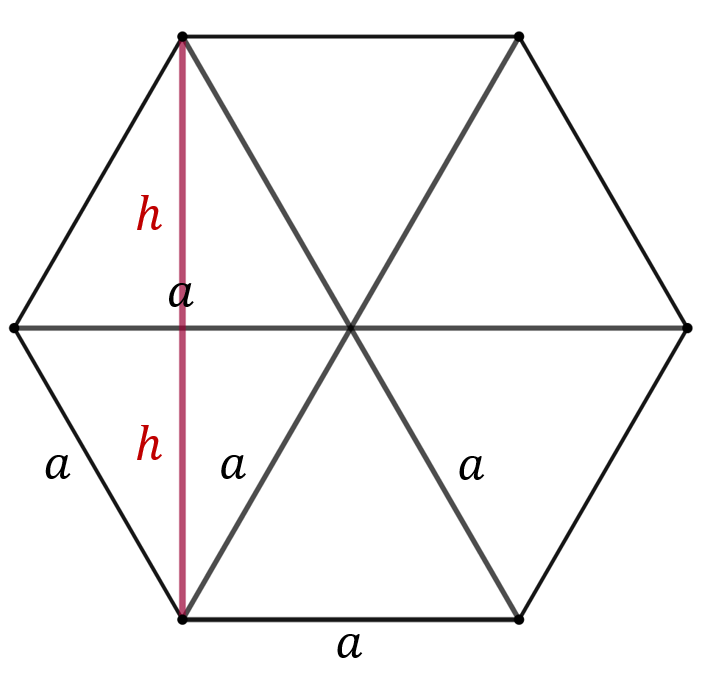 Zatem: \[ P_p = 6\cdot \frac{a^2\sqrt{3}}{4}=\frac{3\sqrt{3}}{2} a^2. \] Wysokość tego trójkąta równobocznego to: \[h=\frac{a\sqrt{3}}{2}\] Zróbmy rysunek całego graniastosłupa:
Zatem: \[ P_p = 6\cdot \frac{a^2\sqrt{3}}{4}=\frac{3\sqrt{3}}{2} a^2. \] Wysokość tego trójkąta równobocznego to: \[h=\frac{a\sqrt{3}}{2}\] Zróbmy rysunek całego graniastosłupa: 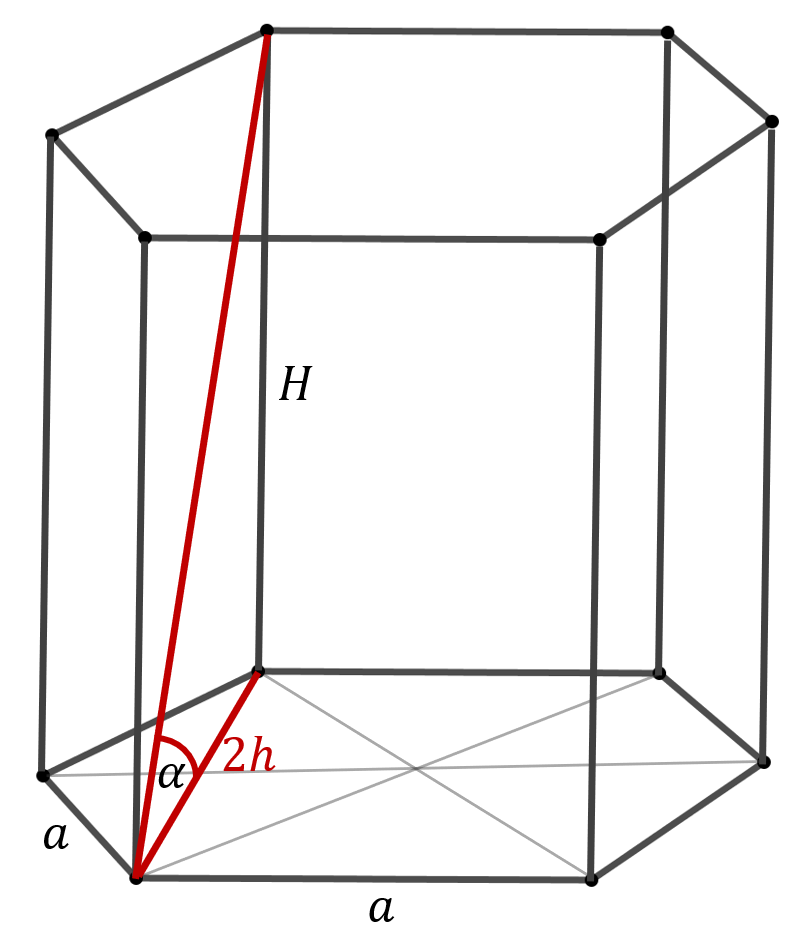
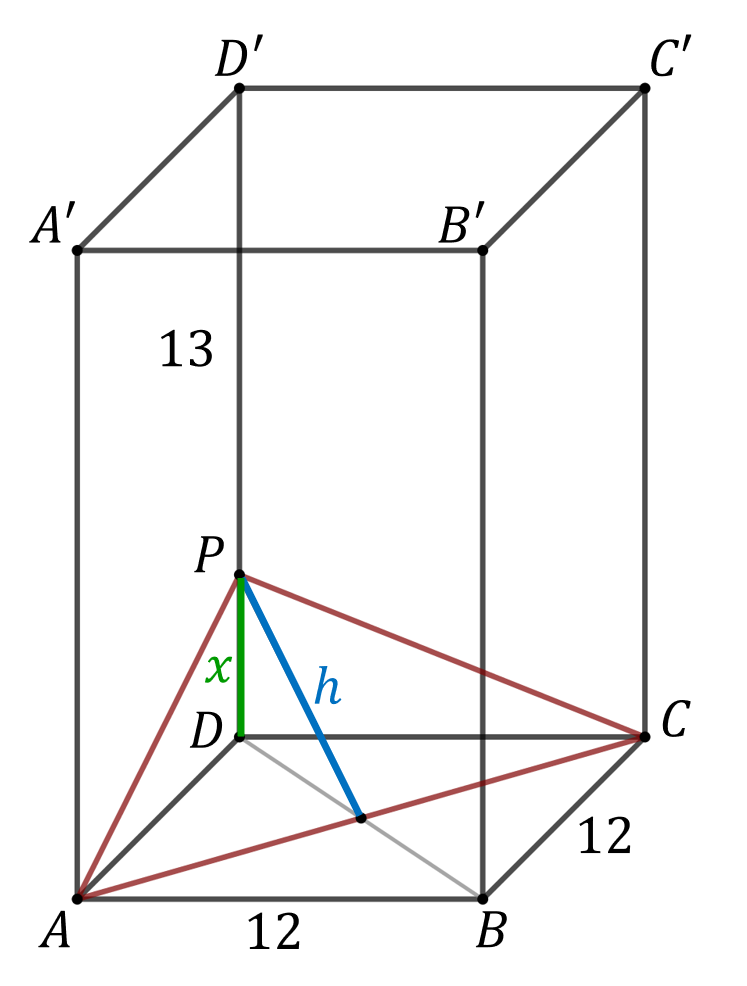 Przekątna \(AC\) ma długość \(12\sqrt{2}\). Zatem: \[P_{ACP}=\frac{1}{2}12\sqrt{2}\cdot h=6\sqrt{2}h\] Z treści zadania wiemy, że \(P_{ACP}=54\sqrt{2}\). Zatem: \[6\sqrt{2}h=54\sqrt{2}\\[6pt] h=9\] Połowa przekątnej podstawy jest równa \(6\sqrt{2}\). Zatem z twierdzenia Pitagorasa: \[x^2=9^2-(6\sqrt{2})^2\\[6pt] x^2 = 81-72\\[6pt] x^2 = 9\\[6pt] x=3\] Zatem szukana wysokość to: \[H=|DD'|=3+13=16\]
Przekątna \(AC\) ma długość \(12\sqrt{2}\). Zatem: \[P_{ACP}=\frac{1}{2}12\sqrt{2}\cdot h=6\sqrt{2}h\] Z treści zadania wiemy, że \(P_{ACP}=54\sqrt{2}\). Zatem: \[6\sqrt{2}h=54\sqrt{2}\\[6pt] h=9\] Połowa przekątnej podstawy jest równa \(6\sqrt{2}\). Zatem z twierdzenia Pitagorasa: \[x^2=9^2-(6\sqrt{2})^2\\[6pt] x^2 = 81-72\\[6pt] x^2 = 9\\[6pt] x=3\] Zatem szukana wysokość to: \[H=|DD'|=3+13=16\]