Różne zadania z ostrosłupów

Drukuj

Poziom podstawowy

Ostrosłup ma \(18\) wierzchołków. Liczba wszystkich krawędzi tego ostrosłupa jest równa

A.\( 11 \)

B.\( 18 \)

C.\( 27 \)

D.\( 34 \)

Dany jest sześcian \(ABCDEFGH\). Siatką ostrosłupa czworokątnego \(ABCDE\) jest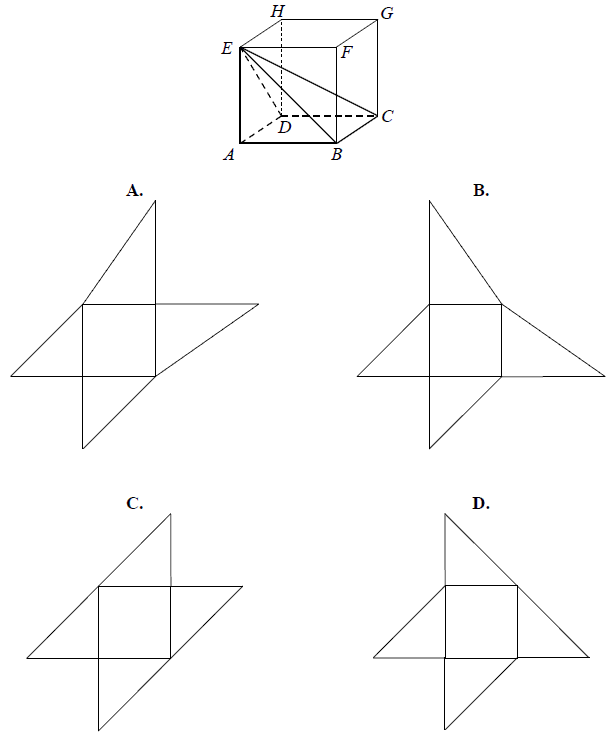

Podstawą ostrosłupa \(ABCD\) jest trójkąt \(ABC\). Krawędź \(AD\) jest wysokością ostrosłupa (zobacz rysunek).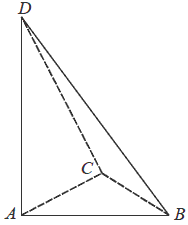

Oblicz objętość ostrosłupa \(ABCD\), jeśli wiadomo, że \(AD = 12\), \(BC = 6\), \(BD = CD = 13\).

\(V=48\)

Podstawą ostrosłupa \(ABCDS\) jest romb \(ABCD\) o boku długości \(4\). Kąt \(ABC\) rombu ma miarę \(120^\circ \) oraz \(|AS|=|CS|=10\) i \(|BS|=|DS|\). Oblicz sinus kąta nachylenia krawędzi \(BS\) do płaszczyzny podstawy ostrosłupa.

\(\sin \alpha =\sqrt{\frac{22}{23}}\)

Podstawą ostrosłupa \(ABCDW\) jest prostokąt \(ABCD\). Krawędź boczna \(DW\) jest wysokością tego ostrosłupa. Krawędzie boczne \(AW\), \(BW\) i \(CW\) mają następujące długości: \(|AW| = 6\), \(|BW| = 9\), \(|CW| = 7\). Oblicz objętość tego ostrosłupa.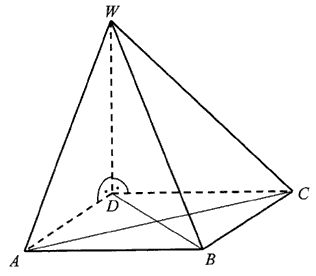

\(8\sqrt{10}\)

Podstawą ostrosłupa \(ABCDS\) jest kwadrat \(ABCD\). Wysokość \(SE\) ściany bocznej \(ADS\) jest jednocześnie wysokością ostrosłupa, a punkt \(E\) jest środkiem krawędzi \(AD\) (zobacz rysunek). Pole ściany \(ADS\) jest równe \(12\) cm², a objętość ostrosłupa jest równa \(48\) cm³. Oblicz miarę kąta nachylenia krawędzi bocznej \(CS\) do płaszczyzny podstawy ostrosłupa. Wynik zaokrąglij do \(1^\circ \).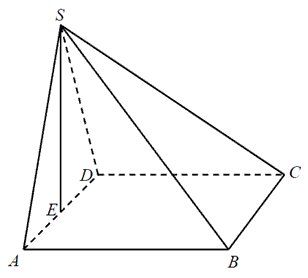

\(31^\circ \)

Podstawą ostrosłupa \(ABCDE\) jest kwadrat \(ABCD\). Punkt \(F\) jest środkiem krawędzi \(AD\), odcinek \(EF\) jest wysokością ostrosłupa (patrz rysunek). Oblicz objętość ostrosłupa, jeśli wiadomo, że \(|AE|=15\), \(|BE|=17\).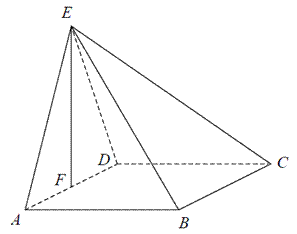

\(\frac{64\sqrt{209}}{3}\)

Jeżeli ostrosłup ma \( 10 \) krawędzi, to liczba ścian bocznych jest równa

A.\(5 \)

B.\(7 \)

C.\(8 \)

D.\(10 \)

Ostrosłup i graniastosłup mają równe pola podstaw i równe wysokości. Objętość ostrosłupa jest równa \( 81\sqrt{3} \). Objętość graniastosłupa jest równa

A.\(27 \)

B.\(27\sqrt{3} \)

C.\(243 \)

D.\(243\sqrt{3} \)

Z sześcianu \( ABCDEFGH \) o krawędzi długości \( a \) odcięto ostrosłup \( ABDE \) (zobacz rysunek).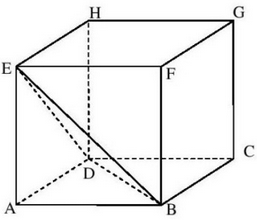

Ile razy objętość tego ostrosłupa jest mniejsza od objętości pozostałej części sześcianu?

A.\( 2 \) razy

B.\( 3 \) razy

C.\( 4 \) razy

D.\( 5 \) razy

Na rysunkach poniżej przedstawiono siatki dwóch ostrosłupów.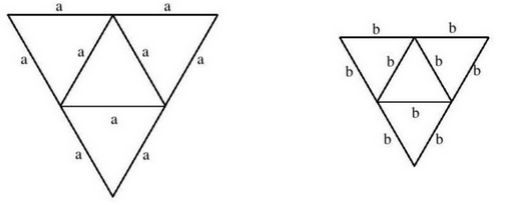

Pole powierzchni całkowitej ostrosłupa o krawędzi \( a \) jest dwa razy większe od pola powierzchni całkowitej ostrosłupa o krawędzi \( b \). Ile razy objętość ostrosłupa o krawędzi \( a \) jest większa od objętości ostrosłupa o krawędzi \( b \)?

A.\( \sqrt{2} \)

B.\( 2 \)

C.\( 2\sqrt{2} \)

D.\( 4 \)

Podstawą ostrosłupa \(ABCDS\) jest prostokąt, którego boki pozostają w stosunku \(3 : 4\), a pole jest równe \(192\) (zobacz rysunek). Punkt \(E\) jest wyznaczony przez przecinające się przekątne podstawy, a odcinek \(SE\) jest wysokością ostrosłupa. Każda krawędź boczna tego ostrosłupa jest nachylona do płaszczyzny podstawy pod kątem \(30^\circ\). Oblicz objętość ostrosłupa.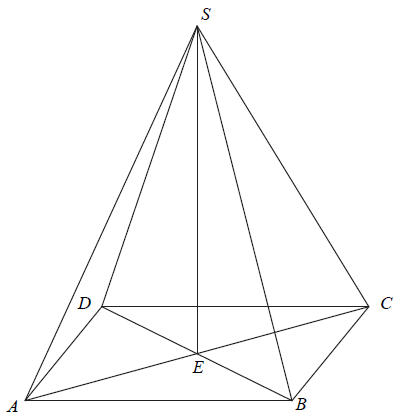

\(V=\frac{640\sqrt{3}}{3}\)

Poziom rozszerzony

W ostrosłupie \(ABCS\) podstawa \(ABC\) jest trójkątem równobocznym o boku długości \(a\). Krawędź \(AS\) jest prostopadła do płaszczyzny podstawy. Odległość wierzchołka \(A\) od ściany \(BCS\) jest równa \(d\). Wyznacz objętość tego ostrosłupa.

\(V=\frac{a^3d}{4\sqrt{3a^2-4d^2}}\)