Monotoniczność funkcji liniowej

Poziom podstawowy

Funkcja liniowa \(f(x)=ax+b\) jest:

rosnąca jeżeli \(a \gt 0\),
malejąca jeżeli \(a \lt 0\),
stała jeżeli \(a = 0\).

Przykład wykresu funkcji liniowej rosnącej, czyli takiej dla której \(a \gt 0\).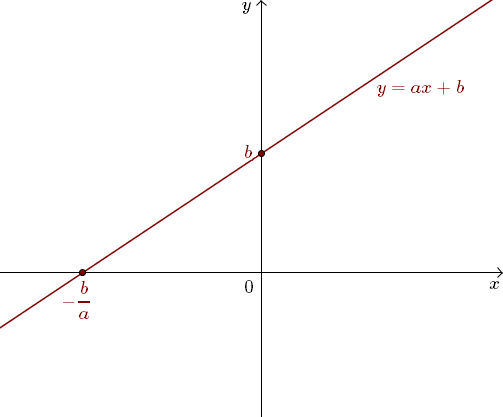

Dla jakiego parametru \(m\) funkcja \(f(x)=(2m-1)x+3\) jest rosnąca?

Funkcja \(f\) jest rosnąca, jeżeli: \[\begin{split} 2m-1&\gt0\\[6pt] 2m&\gt1\\[6pt] m&\gt\frac{1}{2} \end{split}\] Zatem funkcja \(f\) jest rosnąca dla \(m \gt \frac{1}{2}\).

Dla jakiego parametru \(m\) funkcja \(f(x)=3mx+m+1\) jest malejąca?

Funkcja \(f\) jest malejąca, jeżeli: \[\begin{split} 3m&\lt0\\[6pt] m&\lt 0 \end{split}\] Zatem funkcja \(f\) jest malejąca dla \(m \lt 0\).

Funkcja liniowa \(f(x)=(m+2)x+2m\) jest rosnąca, gdy

A.\( m<-2 \)

B.\( m\lt 2 \)

C.\( m>-2 \)

D.\( m>-4 \)

Funkcja liniowa \(f(x)=(m-2)x-11\) jest rosnąca dla

A.\( m>2 \)

B.\( m>0 \)

C.\( m\lt 13 \)

D.\( m\lt 11 \)

Funkcja liniowa \(f(x)=(m^2-1)x-7\) jest malejąca, jeśli:

A.\( m\in \mathbb{R} \)

B.\( m\in (-\infty , -1) \)

C.\( m\in (-1, 1) \)

D.\( m\in (-\infty , 0) \)

Wskaż \(m\), dla którego funkcja liniowa \(\ f(x)=(m−1)x+6\ \) jest rosnąca

A.\( m=-1 \)

B.\( m=0 \)

C.\( m=1 \)

D.\( m=2 \)

Funkcja liniowa \( f(x)=(m^2-4)x+2 \) jest malejąca, gdy

A.\(m\in (-\infty,-2) \)

B.\(m\in (2,+\infty) \)

C.\(m\in \lbrace -2,2 \rbrace \)

D.\(m\in (-2,2) \)

Funkcja liniowa \(f\) określona wzorem \(f(x)=(2m-5)x+22\) jest rosnąca dla

A.\( m\gt\frac{2}{5} \)

B.\( m\gt2{,}5 \)

C.\( m\gt0 \)

D.\( m\gt2 \)

Funkcja \(f\) jest określona dla każdej liczby rzeczywistej \(x\) wzorem \(f(x)=(m\sqrt{5}-1)x+3\). Ta funkcja jest rosnąca dla każdej liczby \(m\) spełniającej warunek

A.\( m\gt\frac{1}{\sqrt{5}} \)

B.\( m\gt1-\sqrt{5} \)

C.\( m\lt\sqrt{5}-1 \)

D.\( m\lt\frac{1}{\sqrt{5}} \)

Funkcja liniowa \(f\) jest określona wzorem \(f(x)=(-2 k+3) x+k-1\), gdzie \(k \in \mathbb{R}\).

Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.

Funkcja \(f\) jest malejąca dla każdej liczby \(k\) należącej do przedziału

A.\((-\infty, 1)\)

B.\(\left(-\infty,-\frac{3}{2}\right)\)

C.\((1,+\infty)\)

D.\(\left(\frac{3}{2},+\infty\right)\)

Wskaż \(m\), dla którego funkcja liniowa określona wzorem \(\ f(x)=(m - 1)x+3\ \) jest stała.

A.\( m=1 \)

B.\( m=2 \)

C.\( m=3 \)

D.\( m=-1 \)

Funkcja liniowa \( f(x)=ax+b\ \) jest rosnąca i ma dodatnie miejsce zerowe. Stąd wynika, że

A.\(a>0\) i \( b>0 \)

B.\(a\lt 0\) i \( b\lt 0 \)

C.\(a\lt 0\) i \( b>0 \)

D.\(a>0\) i \( b\lt 0 \)

Funkcja liniowa \(f(x)=(m^2-3)x+2\) jest rosnąca wtedy, gdy:

A.\( m \in (-\sqrt{3}, \sqrt{3}) \)

B.\( m \in (-\infty, -\sqrt{3})\cup (\sqrt{3}, \infty ) \)

C.\( m \in \{-\sqrt{3}, \sqrt{3}\} \)

D.\( m \in (\sqrt{3}, \infty ) \)

Funkcja liniowa \(f\) określona jest wzorem \(f(x) = \frac{1}{3}x - 1\), dla wszystkich liczb rzeczywistych \(x\). Wskaż zdanie prawdziwe.

A.Funkcja \(f\) jest rosnąca i jej wykres przecina oś \(Oy\) w punkcie \(P = \Biggl( 0, \frac{1}{3} \Biggl) \).

B.Funkcja \(f\) jest rosnąca i jej wykres przecina oś \(Oy\) w punkcie \(P = ( 0, -1) \).

C.Funkcja \(f\) jest malejąca i jej wykres przecina oś \(Oy\) w punkcie \(P = \Biggl( 0, \frac{1}{3} \Biggl) \).

D.Funkcja \(f\) jest malejąca i jej wykres przecina oś \(Oy\) w punkcie \(P = ( 0, -1) \).