Pojęcie miary kąta i jego uogólnienie

Drukuj

Poziom rozszerzony

Definicja

Kąt jednostkowy - to kąt któremu przyporządkowujemy liczbę \(1\).

Jeżeli kąty mierzymy w stopniach, to kątem jednostkowym jest kąt o mierze \(1^\circ \).

Definicja

Miara kąta - to liczba określająca ile razy kąt jednostkowy mieści się w danym kącie.

Niektóre kąty mają specjalne nazwy, np.: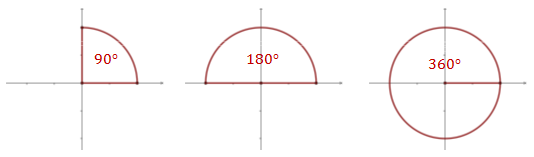

kąt zerowy - to kąt o mierze \(0^\circ\),
kąt prosty - to kąt o mierze \(90^\circ\),
kąt półpełny - to kąt o mierze \(180^\circ\),
kąt pełny - to kąt o mierze \(360^\circ\),
kąt ostry - to kąt o mierze mniejszej niż \(90^\circ\),
kąt rozwarty - to kąt o mierze większej niż \(90^\circ\),
kąt wypukły - to kąt o mierze mniejszej lub równej \(180^\circ\),
kąt wklęsły - to kąt o mierze większej niż \(180^\circ\) i mniejszej niż \(360^\circ \).

W praktyce najczęściej spotykamy się z kątami z przedziału \(\left \langle 0^\circ ; 360^\circ \right \rangle\). Można jednak ten zakres rozszerzyć i rozważać kąty o miarach np.: \(400^\circ , 680^\circ \text{ lub } -510^\circ \). Za chwilę zobaczymy jak należy interpretować takie "większe" kąty.

Zacznijmy od tego, że zaznaczymy dowolny kąt w układzie współrzędnych.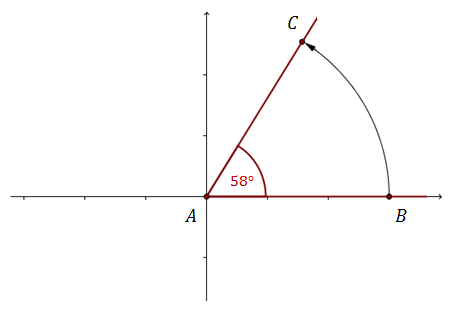

Zauważmy, że powyższy kąt o mierze \(58^\circ \) uzyskaliśmy poprzez obrót półprostej \(AB\) wokół punktu \(A\) (drogę jaką pokonał punkt \(B\) pokazuje czarna strzałka).
Półprostą \(AB\) obróciliśmy w kierunku przeciwnym do ruchu wskazówek zegara i dzięki temu otrzymaliśmy kąt dodatni.
Jeżeli obracamy półprostą w kierunku zgodnym z ruchem wskazówek zegara, to otrzymujemy kąty ujemne. Przykładowo: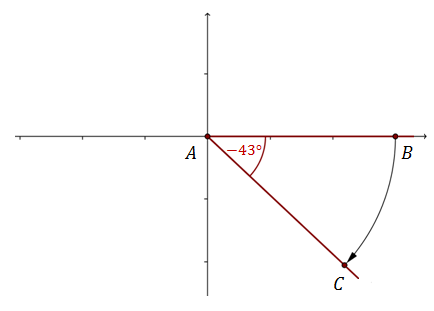

Więcej przykładów:

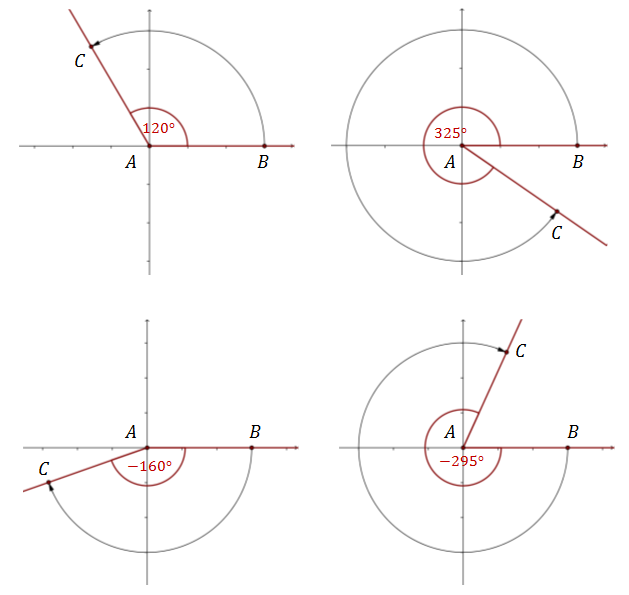
Półprostą \(AB\) możemy obrócić dowolnie wiele razy i jeszcze o pewien kąt mniejszy od kąta pełnego. Jeżeli na przykład obrócimy ją całkowicie trzy razy i jeszcze o kąt \(50^\circ \), to otrzymamy kąt o mierze \(3\cdot 360^\circ +50^\circ = 1130^\circ \).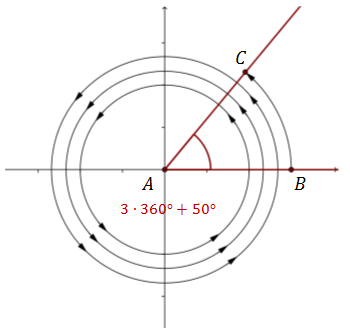

Jak widać na powyższym rysunku kąt o mierze \(1130^\circ \) jest wyznaczony przez te same ramiona \(AB\text{ i }AC\) co kąt o mierze \(50^\circ \).

Fakt

Jeżeli ramiona kąta \(\alpha \) pokrywają się z ramionami kąta \(\beta \), to wówczas kąty te możemy ze sobą utożsamiać.

Oto kilka przykładów:

Ramiona kąta \(\alpha = 40^\circ \) są ramionami kąta \(\beta =400^\circ \), bo \(400^\circ =360^\circ +40^\circ \).
Ramiona kąta \(\alpha = 40^\circ \) są ramionami kąta \(\beta =760^\circ \), bo \(760^\circ =2\cdot 360^\circ +40^\circ \).
Ramiona kąta \(\alpha = 40^\circ \) są ramionami kąta \(\beta =1120^\circ \), bo \(1120^\circ =3\cdot 360^\circ +40^\circ \).
Ramiona kąta \(\alpha = 40^\circ \) są ramionami kąta \(\beta =1480^\circ \), bo \(1480^\circ =4\cdot 360^\circ +40^\circ \).
Ramiona kąta \(\alpha = 40^\circ \) są ramionami kąta \(\beta =-320^\circ \), bo \(-320^\circ =(-1)\cdot 360^\circ +40^\circ \).
Ramiona kąta \(\alpha = 40^\circ \) są ramionami kąta \(\beta =-680^\circ \), bo \(-680^\circ =(-2)\cdot 360^\circ +40^\circ \).

Fakt

Każdy kąt można utożsamić z kątem z przedziału \(\left \langle 0^\circ ;360^\circ \right \rangle\).

Oto kilka przykładów:

\(450^\circ =90^\circ +360^\circ \)
\(600^\circ =240^\circ +360^\circ \)
\(2000^\circ =200^\circ +5\cdot 360^\circ \)
\(5471^\circ =71^\circ +15\cdot 360^\circ \)
\(-1425^\circ =15^\circ -4\cdot 360^\circ \)
\(-2000^\circ =160^\circ -6\cdot 360^\circ \)