Podobieństwo trójkątów
Trójkąty podobne - to dwa trójkąty, których odpowiednie boki są parami proporcjonalne. Oznacza to, że stosunki odpowiednich boków są równe. 
Na powyższym rysunku trójkąty \(ABC\) i \(A'B'C'\) są podobne. Zapiszemy to tak: \[\triangle ABC \sim \triangle A'B'C'\] Stosunki odpowiednich boków w powyższych trójkątach są równe, co zapiszemy tak: \[\frac{|AB|}{|A'B'|}=\frac{|BC|}{|B'C'|}=\frac{|AC|}{|A'C'|}\] Trójkąty podobne mają kąty o takiej samej mierze. Na powyższym rysunku oba trójkąty mają kąty \(\alpha, \beta, \gamma\).
Na powyższym rysunku trójkąty \(ABC\) i \(A'B'C'\) są podobne. Zapiszemy to tak: \[\triangle ABC \sim \triangle A'B'C'\] Stosunki odpowiednich boków w powyższych trójkątach są równe, co zapiszemy tak: \[\frac{|AB|}{|A'B'|}=\frac{|BC|}{|B'C'|}=\frac{|AC|}{|A'C'|}\] Trójkąty podobne mają kąty o takiej samej mierze. Na powyższym rysunku oba trójkąty mają kąty \(\alpha, \beta, \gamma\). Cechy podobieństwa trójkątów
Trójkąty są podobne, jeśli zachodzi dowolny z poniższych warunków:- Cecha BBB (Bok-Bok-Bok) - stosunki długości odpowiednich boków są równe,
- Cecha KKK (Kąt-Kąt-Kąt) - miary odpowiednich kątów są równe,
- Cecha BKB (Bok-Kąt-Bok) - stosunki długości dwóch par boków są równe i miary kątów między tymi bokami są równe,
Czy trójkąty o bokach długości: \(2,3,4\) oraz \(9,6,12\) są podobne?
Korzystamy z cechy podobieństwa trójkątów BBB. Sprawdzamy czy stosunki najkrótszych boków, średnich boków oraz najdłuższych boków jest taki sam, tzn. czy zachodzi równość: \[\frac{2}{6}=\frac{3}{9}=\frac{4}{12}\] Powyższa równość jest prawdziwa, ponieważ każdy z ułamków po skróceniu jest równy \(\frac{1}{3}\): \[\frac{1}{3}=\frac{1}{3}=\frac{1}{3}\] Zatem trójkąty są podobne.
Zbadaj czy trójkąty \(ABC\) i \(DEF\) są podobne.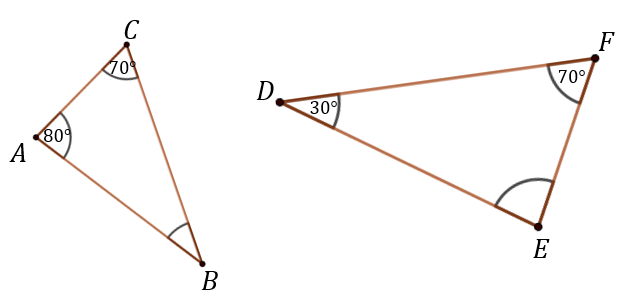 
Sprawdzimy cechę podobieństwa trójkątów KKK.
Liczymy trzeci kąt trójkąta \(ABC\): \[|\sphericalangle ABC|=180^\circ -(80^\circ +70^\circ )=180^\circ -150^\circ =30^\circ \] Teraz liczymy trzeci kąt trójkąta \(DEF\): \[|\sphericalangle DEF|=180^\circ -(30^\circ +70^\circ )=180^\circ -100^\circ =80^\circ \] Oba trójkąty mają kąty o miarach: \(30^\circ, 70^\circ\) oraz \(80^\circ \), zatem z cechy KKK są podobne.
Możemy zapisać podobieństwo trójkątów: \[\triangle ABC\sim \triangle EDF\] Zwróć uwagę, że przy zapisywaniu podobieństwa trójkątów, wierzchołki wypisujemy w takiej kolejności, aby kolejne literki odpowiadały tym samym kątom. Dzięki takiej staranności, można później zapisywać stosunki odpowiednich boków, patrząc jedynie na zapisane podobieństwo \(\triangle ABC\sim \triangle EDF\). Przykładowo: \[\frac{|AB|}{|ED|}=\frac{|AC|}{|EF|}\]
Liczymy trzeci kąt trójkąta \(ABC\): \[|\sphericalangle ABC|=180^\circ -(80^\circ +70^\circ )=180^\circ -150^\circ =30^\circ \] Teraz liczymy trzeci kąt trójkąta \(DEF\): \[|\sphericalangle DEF|=180^\circ -(30^\circ +70^\circ )=180^\circ -100^\circ =80^\circ \] Oba trójkąty mają kąty o miarach: \(30^\circ, 70^\circ\) oraz \(80^\circ \), zatem z cechy KKK są podobne.
Możemy zapisać podobieństwo trójkątów: \[\triangle ABC\sim \triangle EDF\] Zwróć uwagę, że przy zapisywaniu podobieństwa trójkątów, wierzchołki wypisujemy w takiej kolejności, aby kolejne literki odpowiadały tym samym kątom. Dzięki takiej staranności, można później zapisywać stosunki odpowiednich boków, patrząc jedynie na zapisane podobieństwo \(\triangle ABC\sim \triangle EDF\). Przykładowo: \[\frac{|AB|}{|ED|}=\frac{|AC|}{|EF|}\]
Trójkąt \(ABC\) ma boki długości: \(4,12,x\), a trójkąt \(PQR\) ma boki długości \(5,13,15\). Wiadomo, że trójkąty \(ABC\) i \(PQR\) są podobne. Oblicz \(x\).
Zauważmy, że w trójkącie \(ABC\) bok \(x\) musi być bokiem średnim co do długości.
Skoro trójkąty są podobne, to stosunki ich odpowiednich boków muszą być równe, czyli: \[\frac{4}{5}=\frac{12}{15}=\frac{x}{13}\] Rozwiązujemy równanie: \[\begin{split} \frac{4}{5}&=\frac{x}{13}\\[6pt] 5x&=4\cdot 13\\[6pt] x&=\frac{52}{5} \end{split}\]
Skoro trójkąty są podobne, to stosunki ich odpowiednich boków muszą być równe, czyli: \[\frac{4}{5}=\frac{12}{15}=\frac{x}{13}\] Rozwiązujemy równanie: \[\begin{split} \frac{4}{5}&=\frac{x}{13}\\[6pt] 5x&=4\cdot 13\\[6pt] x&=\frac{52}{5} \end{split}\]
W tym nagraniu wideo pokazuję co to są trókąty podobne.
W tym nagraniu wideo pokazuję jak poprawnie zapisywać podobieństwo trójkątów
Odcinki \(AB\) i \(CD\) są równoległe, trójkąt \(ABE\) jest równoboczny i \(|AB|=5\) oraz \(|BD|=2\) (zobacz rysunek).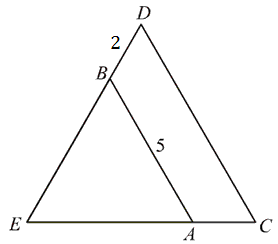 
Obwód czworokąta \(ACDB\) wynosi:
Obwód czworokąta \(ACDB\) wynosi: A.\( 12 \)
B.\( 14 \)
C.\( 16 \)
D.\( 18 \)
Proste \(AD\) i \(BC\) są równoległe. Długości odcinków \(ED\), \(DC\) oraz \(AB\) podane są na rysunku. Długość odcinka \(EA\) jest równa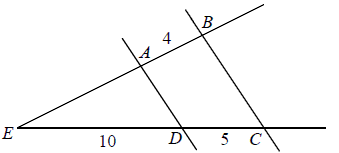 
A.\( 4 \)
B.\( 8 \)
C.\( 9 \)
D.\( 10 \)
Odcinki \( BC\) i \(DE \) są równoległe. Długości odcinków \( AC, CE \) i \( BC \) są podane na rysunku. Długość odcinka \( DE \) jest równa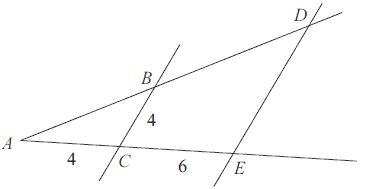 
A.\(6 \)
B.\(8 \)
C.\(10 \)
D.\(12 \)
Czy poniższe trójkąty są podobne? 
Długość odcinka \( AB \), równoległego do odcinka \( CD \), jest równa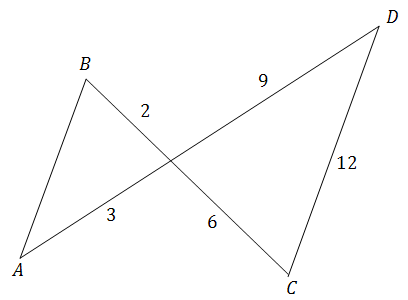 
A.\( 6 \)
B.\( 3 \)
C.\( 2 \)
D.\( 4 \)
Jeżeli trójkąty \( ABC \) i \( A'B'C' \) są podobne, a ich pola są, odpowiednio, równe \( 25 \) cm2 i \( 50 \) cm2, to skala podobieństwa \( \frac{A'B'}{AB} \) jest równa
A.\(2 \)
B.\(\frac{1}{2} \)
C.\(\sqrt{2} \)
D.\(\frac{\sqrt{2}}{2} \)
Odcinki \( BC \) i \( DE \) są równoległe i \( |AE|=4 \), \( |DE|=3 \) (zobacz rysunek). Punkt \( D \) jest środkiem odcinka \( AB \). Długość odcinka \( BC \) jest równa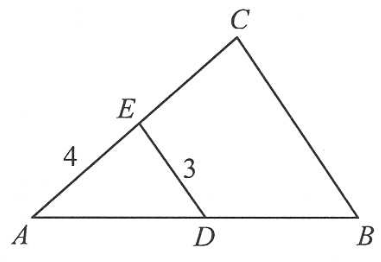 
A.\(4 \)
B.\(6 \)
C.\(8 \)
D.\(16 \)
Przedstawione na rysunku trójkąty są podobne.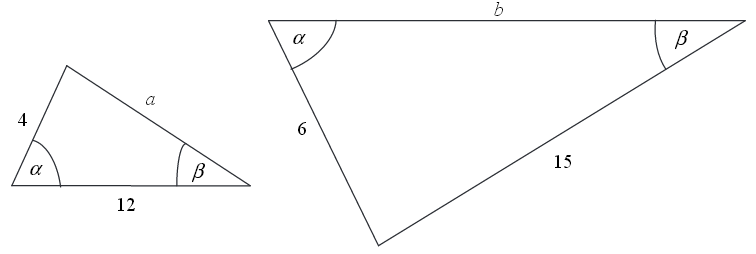 
Wówczas
Wówczas A.\( a=13 \), \(b=17 \)
B.\( a=10 \), \(b=18 \)
C.\( a=9 \), \(b=19 \)
D.\( a=11 \), \(b=13 \)
Obwody dwóch trójkątów podobnych, których pola pozostają w stosunku \(1:4\), mogą być równe
A.\( 9 \) i \(36\)
B.\( 18 \) i \(36\)
C.\( 9 \) i \(144\)
D.\( 18 \) i \(144\)
Trójkąt \(T\) jest podobny do trójkąta \(T_1\) w skali \(k=\frac{1}{6}\), a trójkąt \(T_2\) jest podobny do trójkąta \(T\) w skali \(k=3\). Pole trójkąta \(T_2\) jest równe \(24\). Trójkąt \(T_1\) ma pole równe
A.\( 12 \)
B.\( 48 \)
C.\( 72 \)
D.\( 96 \)
Przedstawione na rysunku trójkąty \(ABC\) i \(PQR\) są podobne. Bok \(AB\) trójkąta \(ABC\) ma długość 
A.\( 8 \)
B.\( 8{,}5 \)
C.\( 9{,}5 \)
D.\( 10 \)
Trójkąt \(ABC\) jest podobny do trójkąta \(A'B'C'\) w skali \(\frac{5}{2}\), przy czym \(|AB|=\frac{5}{2}|A'B'|\). Stosunek pola trójkąta \(ABC\) do pola trójkąta \(A'B'C'\) jest równy
A.\( \frac{4}{25} \)
B.\( \frac{2}{5} \)
C.\( \frac{5}{2} \)
D.\( \frac{25}{4} \)
Trójkąty \(ABC\) i \(DEF\) są podobne. Obwód trójkąta \(ABC\) jest równy \(16\), a jego pole \(12\). Pole trójkąta \(DEF\) jest równe \(60\). Zatem obwód trójkąta \(DEF\) jest równy:
A.\( 80 \)
B.\( 16\sqrt{5} \)
C.\( \frac{16\sqrt{5}}{5} \)
D.\( \frac{16}{5} \)
Dany jest trójkąt o bokach długości: \(2\sqrt{5}\), \(3\sqrt{5}\), \(4\sqrt{5}\). Trójkątem podobnym do tego trójkąta jest trójkąt, którego boki mają długości
A.\( 10, 15, 20 \)
B.\( 20, 45, 80 \)
C.\( \sqrt{2}, \sqrt{3}, \sqrt{4} \)
D.\( \sqrt{5}, 2\sqrt{5}, 3\sqrt{5} \)
Odcinki \(AD\) i \(BE\) przecinają się w punkcie \(C\). W trójkątach \(ABC\) i \(CDE\) zachodzą związki: \(|\sphericalangle CAB|=|\sphericalangle CED|\), \(|AC|=5\), \(|BC|=3\), \(|CE|=10\) (zobacz rysunek). Wykaż, że trójkąty \(ABC\) i \(CDE\) są podobne. Oblicz długość boku \(CD\).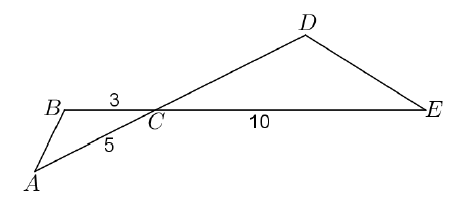 
Dany jest trójkąt prostokątny \(ABC\). Na przyprostokątnych \(AC\) i \(AB\) tego trójkąta obrano odpowiednio punkty \(D\) i \(G\). Na przeciwprostokątnej \(BC\) wyznaczono punkty \(E\) i \(F\) takie, że \(|\sphericalangle DEC|=|\sphericalangle BGF|=90^\circ \) (zobacz rysunek). Wykaż, że trójkąt \(CDE\) jest podobny do trójkąta \(FBG\). 
Trójkąty prostokątne \(ABC\) i \(DEF\) są podobne. Przyprostokątne trójkąta \(ABC\) mają długości \(5\) i \(12\), a przeciwprostokątna trójkąta\(DEF\) ma długość \(26\). Wyznacz pole trójkąta \(DEF\).