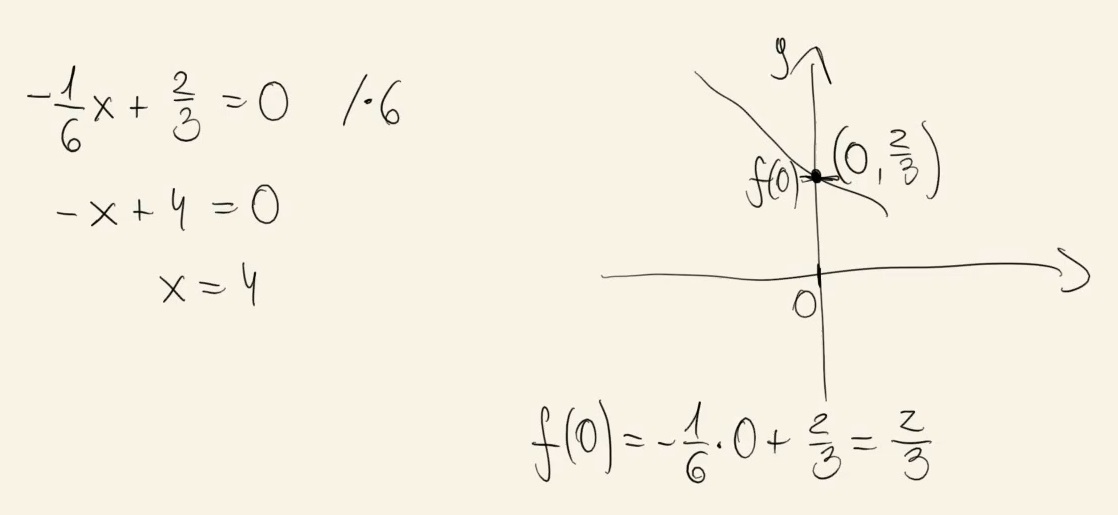Miejsce zerowe funkcji liniowej

Poziom podstawowy

Miejsce zerowe funkcji liniowej obliczamy przyrównując wzór funkcji do zera.

Miejsce zerowe funkcji liniowej \(f(x)=ax+b\), to argument \(x\) spełniający równanie: \[ax+b=0\] Z powyższego równania wynika bezpośredni wzór: \[x=-\frac{b}{a}\]

Wyznacz miejsce zerowe funkcji \(f(x) = 5x - 15\).

Przyrównujemy wzór funkcji do zera: \[\begin{split} 5x - 15 &= 0\\[6pt] 5x &= 15\\[6pt] x &= 3\\[6pt] \end{split}\] Zatem miejscem zerowym podanej funkcji jest \(x = 3\).

Miejscem zerowym funkcji liniowej określonej wzorem \(f(x)=-\frac{2}{3}x+4\) jest

A.\( 0 \)

B.\( 6 \)

C.\( 4 \)

D.\( -6 \)

Dana jest funkcja liniowa \(f(x)=\frac{3}{4}x+6\). Miejscem zerowym tej funkcji jest liczba

A.\( 8 \)

B.\( 6 \)

C.\( -6 \)

D.\( -8 \)

Miejscem zerowym funkcji liniowej \(f\) określonej wzorem \(f(x)=-\frac{1}{3}(x+3)+5\) jest liczba

A.\( (-3) \)

B.\( \frac{9}{2} \)

C.\( 5 \)

D.\( 12 \)

Funkcja liniowa \(f\) jest określona wzorem \(f(x)=21-\frac{7}{3}x\). Miejscem zerowym funkcji \(f\) jest

A.\( -9 \)

B.\( -\frac{7}{3} \)

C.\( 9 \)

D.\( 21 \)

Miejscem zerowym funkcji liniowej \(f(x)=\sqrt{3}(x+1)-12\) jest liczba

A.\( \sqrt{3}-4 \)

B.\( -2\sqrt{3}+1 \)

C.\( 4\sqrt{3}-1 \)

D.\( -\sqrt{3}+12 \)

Miejscem zerowym funkcji \( f(x)=\sqrt{2}\cdot x-\frac{\sqrt{8}}{4} \) jest liczba:

A.\(\frac{1}{2} \)

B.\(\sqrt{2} \)

C.\(-2 \)

D.\(2 \)

Funkcja liniowa określona jest wzorem \(f(x) = -\sqrt{2}x + 4\). Miejscem zerowym tej funkcji jest liczba

A.\( -2\sqrt{2} \)

B.\( \frac{\sqrt{2}}{2} \)

C.\( -\frac{\sqrt{2}}{2} \)

D.\( 2\sqrt{2} \)

Miejscem zerowym funkcji liniowej \(f\) określonej wzorem \(f(x) = 3(x + 1) - 6\sqrt{3}\) jest liczba

A.\( 3 - 6\sqrt{3} \)

B.\( 1 - 6\sqrt{3} \)

C.\( 2\sqrt{3} - 1 \)

D.\( 2\sqrt{3} - \frac{1}{3} \)

\(2\sqrt{3} - 1\)

Funkcja liniowa \(f\) jest określona wzorem \(f(x) = -\frac{1}{6}x+\frac{2}{3}\) .

Oceń prawdziwość poniższych stwierdzeń. Wybierz P, jeśli stwierdzenie jest prawdziwe, albo F - jeśli jest fałszywe.

Miejscem zerowym funkcji \(f\) jest liczba \(4\).	P	F
Punkt przecięcia wykresu funkcji \(f\) z osią \(Oy\) ma współrzędne \(\left(0, -\frac{1}{6}\right)\)	P	F

Liczba \((−2)\) jest miejscem zerowym funkcji liniowej \(f(x)=mx+2\). Wtedy

A.\( m=3 \)

B.\( m=1 \)

C.\( m=-2 \)

D.\( m=-4 \)

Dana jest funkcja \(f(x) = (1 + m^2)x - 5\). Oblicz współczynnik \(m\) jeżeli wiadomo, że \(x = 1\) jest miejscem zerowym funkcji \(f(x)\).

\(m=-2\) lub \(m=2\)

Miejscem zerowym funkcji liniowej \(f(x)=-2x+m+7\) jest liczba \(3\). Wynika stąd, że

A.\( m=7 \)

B.\( m=1 \)

C.\( m=-1 \)

D.\( m=-7 \)

Funkcja liniowa \(f\) określona wzorem \(f(x)=2x+b\) ma takie samo miejsce zerowe, jakie ma funkcja \(g(x)=-3x+4\). Stąd wynika, że

A.\( b=-\frac{8}{3} \)

B.\( b=\frac{4}{3} \)

C.\( b=4 \)

D.\( b=-\frac{3}{2} \)

Liczba \( 1 \) jest miejscem zerowym funkcji liniowej \( f(x)=(2-m)x+1 \). Wynika stąd, że

A.\(m=0 \)

B.\(m=1 \)

C.\(m=2 \)

D.\(m=3 \)

Funkcja liniowa \(f\) jest określona wzorem \(f(x)=(a+1)x+11\), gdzie \(a\) to pewna liczba rzeczywista, ma miejsce zerowe równe \(x=\frac{3}{4}\). Stąd wynika, że

A.\( a=-\frac{41}{3} \)

B.\( a=\frac{41}{3} \)

C.\( a=-\frac{47}{3} \)

D.\( a=\frac{47}{3} \)

Liczba \((-3)\) jest miejscem zerowym funkcji \(f(x)=(2m-1)x+9\). Wtedy

A.\( m=-2 \)

B.\( m=0 \)

C.\( m=2 \)

D.\( m=3 \)

Reszta z dzielenia liczby \(45\) przez \(6\) jest miejscem zerowym funkcji \(f(x)=(m+2)x+15\). Wtedy

A.\( m=-7 \)

B.\( m=-3 \)

C.\( m=0 \)

D.\( m=3 \)

Liczba \(x=-7\) jest miejscem zerowym funkcji liniowej \(f(x)=(3-a)x+7\) dla

A.\( a=-7 \)

B.\( a=2 \)

C.\( a=3 \)

D.\( a=-1 \)

Funkcje liniowe \(f\) oraz \(g\), określone wzorami \(f(x)=3 x+6\) oraz \(g(x)=a x+7\), mają to samo miejsce zerowe.

Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.

Współczynnik \(a\) we wzorze funkcji \(g\) jest równy

A.\(\left(-\frac{7}{2}\right)\)

B.\(\left(-\frac{2}{7}\right)\)

C.\(\frac{2}{7}\)

D.\(\frac{7}{2}\)

Liczba \(1\) jest miejscem zerowym funkcji liniowej \(f(x) = ax + b\), a punkt \(M = (3, -2)\) należy do wykresu tej funkcji. Współczynnik \(a\) we wzorze tej funkcji jest równy

A.\( 1 \)

B.\( \frac{3}{2} \)

C.\( -\frac{3}{2} \)

D.\( -1 \)

Miejscem zerowym funkcji liniowej \(f\) jest liczba \(1\). Wykres tej funkcji przechodzi przez punkt \((-1, 4)\).

Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.

Wzór funkcji \(f\) ma postać

A.\( f(x)=-\frac{1}{2}x+1 \)

B.\( f(x)=-\frac{1}{3}x+\frac{1}{3} \)

C.\( f(x)=-2x+2 \)

D.\( f(x)=-3x+1 \)

Miejsce zerowe funkcji liniowej \(f(x) = x + 3m\) jest większe od \(2\) dla każdej liczby \(m\) spełniającej warunek

A.\( m\lt -\frac{2}{3} \)

B.\( -\frac{2}{3}\lt m\lt \frac{1}{3} \)

C.\( \frac{1}{3}\lt m\lt 1 \)

D.\( m\gt 1 \)

Funkcja liniowa \(f(x)=(1-m^2)x+m-1\) nie ma miejsc zerowych dla

A.\( m=1 \)

B.\( m=0 \)

C.\( m=-1 \)

D.\( m=-2 \)