Miejsca zerowe funkcji
Poziom podstawowy
Definicja
Miejsce zerowe funkcji - to taki argument \(x\) dla którego funkcja przyjmuje wartość \(0\).Wyznacz miejsce zerowe funkcji \(f(x)=5x+2\).
Przyrównujemy wzór funkcji do zera i rozwiązujemy równanie: \[5x+2=0\\[6pt] 5x=-2\\[6pt] x=-\frac{2}{5} \]
Wyznacz miejsce zerowe funkcji \(f(x)=(x-2)(x+3)\).
Przyrównujemy wzór funkcji do zera: \[(x-2)(x+3)=0\] Iloczyn dwóch nawiasów jest równy \(0\) jeżeli jeden albo drugi nawias jest równy \(0\), czyli: \[x-2=0\quad \lor \quad x+3=0 \\[6pt] x=2\quad \lor \quad x=-3\]
Lekcja 1. Miejsca zerowe - wprowadzenie
W tym nagraniu wideo wyjaśniam co to są miejsca zerowe funkcji oraz pokazuję jak je obliczać.
Zadanie 1.
Wyznacz miejsca zerowe następujących funkcji:
\(f(x)=3x-12\)
\(f(x)=3\sqrt{2}-x\)
Zadanie 2.
Wyznacz miejsca zerowe następujących funkcji:
\(f(x)=(x-1)(x+5)\)
\(f(x)=x(4x-\sqrt{2})\)
Zadanie 3.
Wyznacz miejsca zerowe funkcji \(f(x)=13x(1-3x)(\sqrt{2}x-2)(x^2-4)\) .
Zadanie 4.
Wyznacz miejsca zerowe funkcji \(f(x)=4x^2-20x+25\).
Zadanie 5.
Wyznacz miejsca zerowe funkcji \(f(x)=\frac{(x^2+4x+4)(3-x)}{x}\).
Zadanie 6.
Wyznacz miejsca zerowe funkcji \(f(x)=\frac{(x^2-9)(x+2)}{2x+6}\).
Zadanie 7.
Miejscem zerowym funkcji kwadratowej \(y=-(-x-7)(1+x)\) jest
A.\( x=7 \)
B.\( x=1 \)
C.\( x=0 \)
D.\( x=-1 \)
Zadanie 8.
Dany jest wykres funkcji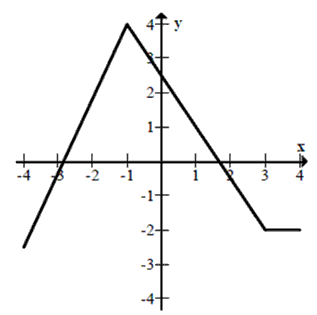 
Ile miejsc zerowych ma ta funkcja w przedziale \(\langle -\pi , 1 \rangle\)?
Ile miejsc zerowych ma ta funkcja w przedziale \(\langle -\pi , 1 \rangle\)? A.\( 0 \)
B.\( 1 \)
C.\( 2 \)
D.\( 3 \)
Zadanie 9.
Miejscami zerowymi funkcji kwadratowej \( y = -3(x-7)(x+2) \) są
A.\(x=7, x=-2 \)
B.\(x=-7, x=-2 \)
C.\(x=7, x=2 \)
D.\(x=-7, x=2 \)
Zadanie 10.
Wskaż wykres funkcji, która w przedziale \( \langle -4, 4 \rangle \) ma dokładnie jedno miejsce zerowe.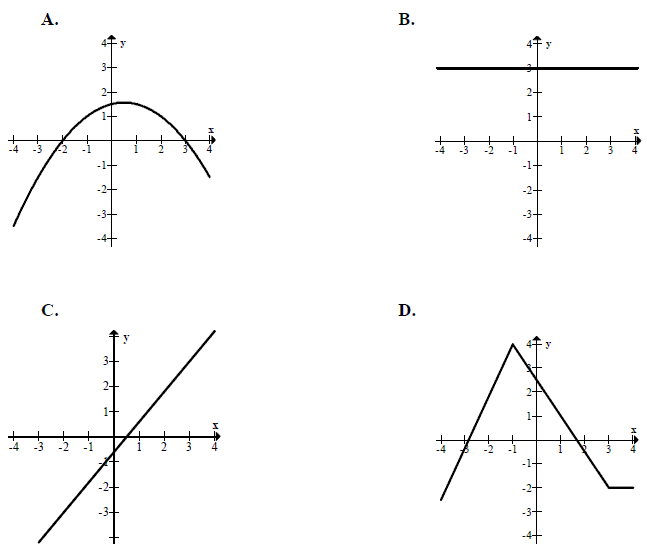 
Zadanie 11.
Funkcja \(f\) jest określona wzorem \( f(x)=\begin{cases} {x-4\ \ \ \quad \text{ dla } x\le 3}\\ {-x+2\quad \text{ dla }x>3} \end{cases} \). Ile miejsc zerowych ma ta funkcja?
A.\( 0 \)
B.\( 1 \)
C.\( 2 \)
D.\( 3 \)
Zadanie 12.
Funkcja liniowa określona jest wzorem \(f(x) = -\sqrt{2}x + 4\). Miejscem zerowym tej funkcji jest liczba
A.\( -2\sqrt{2} \)
B.\( \frac{\sqrt{2}}{2} \)
C.\( -\frac{\sqrt{2}}{2} \)
D.\( 2\sqrt{2} \)
Zadanie 13.
Funkcja \( f \) jest określona wzorem \( f(x)=\begin{cases} -3x+4 &\text{dla }x\lt 1\\ 2x-1 &\text{dla }x\ge 1 \end{cases} \). Ile miejsc zerowych ma ta funkcja?
A.\(0 \)
B.\(1 \)
C.\(2 \)
D.\(3 \)
Zadanie 14.
Oblicz miejsca zerowe funkcji \[f(x)=\begin{cases} 2x+1\quad \text{dla }x\le 0\\ x+2\quad \text{dla }x>0 \end{cases} \]
Zadanie 15.
Miejscem zerowym funkcji \(f\) określonej wzorem \(f(x)=\begin{cases} x^2-1\quad \text{ dla } x\in (-\infty ,-4 \rangle\\ 5x+10\quad \text{ dla } x\in (-4 ,2)\\ x+4\quad \text{ dla } x\in \langle 2,+\infty ) \end{cases} \) jest:
A.\( -4 \)
B.\( -2 \)
C.\( -1 \)
D.\( 1 \)
Zadanie 16.
Liczba \((−2)\) jest miejscem zerowym funkcji liniowej \(f(x)=mx+2\). Wtedy
A.\( m=3 \)
B.\( m=1 \)
C.\( m=-2 \)
D.\( m=-4 \)
Zadanie 17.
Liczba \( 1 \) jest miejscem zerowym funkcji liniowej \( f(x)=(2-m)x+1 \). Wynika stąd, że
A.\(m=0 \)
B.\(m=1 \)
C.\(m=2 \)
D.\(m=3 \)
Zadanie 18.
Miejscem zerowym funkcji liniowej \(f(x)=-2x+m+7\) jest liczba \(3\). Wynika stąd, że
A.\( m=7 \)
B.\( m=1 \)
C.\( m=-1 \)
D.\( m=-7 \)
Zadanie 19.
Dana jest funkcja \(f(x) = (1 + m^2)x - 5\). Oblicz współczynnik \(m\) jeżeli wiadomo, że \(x = 1\) jest miejscem zerowym funkcji \(f(x)\).
Zadanie 20.
Liczba \(x=-7\) jest miejscem zerowym funkcji liniowej \(f(x)=(3-a)x+7\) dla
A.\( a=-7 \)
B.\( a=2 \)
C.\( a=3 \)
D.\( a=-1 \)
Zadanie 21.
Dla jakiego parametru \(m\) liczba \(x=1\) jest miejscem zerowym funkcji \(f(x)=2x^2+mx\)?
A.\( m=-2 \)
B.\( m=2 \)
C.\( m=4 \)
D.\( m=-4 \)
Zadanie 22.
Liczba \(x=2\) jest miejscem zerowym funkcji \(f(x)= mx^2-m-9\) dla
A.\( m=1 \)
B.\( m=2 \)
C.\( m=3 \)
D.\( m=4 \)
Zadanie 23.
Miejscami zerowymi funkcji \( f(x)=\frac{(x-2)(x^2-6x+9)}{x^2-9} \) są liczby:
A.\(2 \)
B.\(2;3 \)
C.\(-2;3 \)
D.\(-3;2;3 \)
Zadanie 24.
Liczba \((-3)\) jest miejscem zerowym funkcji \(f(x)=(2m-1)x+9\). Wtedy
A.\( m=-2 \)
B.\( m=0 \)
C.\( m=2 \)
D.\( m=3 \)
Zadanie 25.
Funkcja \(f(x)=3x(x^2+5)(2-x)(x+1)\) ma dokładnie
A.dwa miejsca zerowe.
B.trzy miejsca zerowe.
C.cztery miejsca zerowe.
D.pięć miejsc zerowych.
Zadanie 26.
Reszta z dzielenia liczby \(45\) przez \(6\) jest miejscem zerowym funkcji \(f(x)=(m+2)x+15\). Wtedy
A.\( m=-7 \)
B.\( m=-3 \)
C.\( m=0 \)
D.\( m=3 \)
Zadanie 27.
Miejscem zerowym funkcji liniowej określonej wzorem \(f(x)=-\frac{2}{3}x+4\) jest
A.\( 0 \)
B.\( 6 \)
C.\( 4 \)
D.\( -6 \)
Zadanie 28.
Na rysunku przedstawiono wykres funkcji \(f\).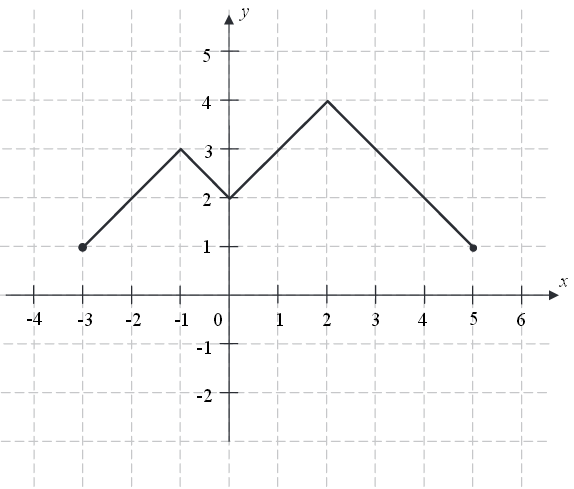 
Funkcja \(h\) określona jest dla \(x\in \langle -3,5 \rangle \) wzorem \(h(x)=f(x)+q\), gdzie \(q\) jest pewną liczbą rzeczywistą. Wiemy, że jednym z miejsc zerowych funkcji \(h\) jest liczba \(x_0=-1\).
Funkcja \(h\) określona jest dla \(x\in \langle -3,5 \rangle \) wzorem \(h(x)=f(x)+q\), gdzie \(q\) jest pewną liczbą rzeczywistą. Wiemy, że jednym z miejsc zerowych funkcji \(h\) jest liczba \(x_0=-1\). a) Wyznacz \(q\).
b) Podaj wszystkie pozostałe miejsca zerowe funkcji \(h\).
b) Podaj wszystkie pozostałe miejsca zerowe funkcji \(h\).
Poziom rozszerzony
Zadanie 29.
Wyznacz wszystkie parametry \(m\), dla których miejscem zerowym funkcji \(f(x)=\frac{m}{x}+31\) jest liczba: \[ \left( 9-32^{\frac{1}{2}}\right)^{\frac{1}{2}} - \left( 9+32^{\frac{1}{2}}\right)^{\frac{1}{2}}\]