Matura podstawowa 2025 - sierpień
Poziom podstawowy
Materiały do pobrania: Arkusz można też wydrukować w prawym górnym rogu strony według własnych preferencji.
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Liczba \(\lvert \sqrt{5}-3\rvert+\lvert \sqrt{5}-1\rvert\) jest równa A.\(2\sqrt{5}-4\)
B.\(2\sqrt{5}+4\)
C.\(2\)
D.\(4\)
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Liczba \(\dfrac{25^{-2}}{125^{-4}}\) jest równa A.\(5^{-16}\)
B.\(5^{-2}\)
C.\(5^{4}\)
D.\(5^{8}\)
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Liczba \(\sqrt[3]{24}+\sqrt[3]{192}\) jest równa A.\(6\)
B.\(3\sqrt[3]{6}\)
C.\(6\sqrt[3]{3}\)
D.\(6\sqrt[3]{6}\)
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Liczba \(\log_{3}2-\log_{3}18\) jest równa A.\((-2)\)
B.\(\left(-\frac12\right)\)
C.\(\frac12\)
D.\(2\)
Wykaż, że liczba \(8^{50}-2^{145}\) jest podzielna przez \(31\).
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Dla każdej liczby rzeczywistej \(x\) i dla każdej liczby rzeczywistej \(y\) wartość wyrażenia \((3x+y)^{2}-(3x-y)^{2}\) jest równa wartości wyrażenia A.\(12xy\)
B.\((-12xy)\)
C.\(2y^{2}\)
D.\(4y^{2}\)
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Zbiorem wszystkich rozwiązań nierówności \[ 3-x\ge \frac{5x-1}{2} \] jest przedział A.\((-\infty,\,1]\)
B.\((-\infty,\,\tfrac{7}{6}]\)
C.\([1,\,+\infty)\)
D.\([\tfrac{7}{6},\,+\infty)\)
Dane jest równanie \[ \frac{3}{3x-7}=\frac{5x}{x-8},\quad \text{gdzie } x\ne \frac{7}{3} \text{ i } x\ne 8. \]
Wyznacz wszystkie rozwiązania tego równania należące do przedziału \(\left(\frac{5}{4},+\infty\right)\). Zapisz obliczenia.
Rozwiąż nierówność \[ -3x^{2}\gt 6x-9. \] Zapisz obliczenia.
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Suma wszystkich rozwiązań równania \((3x-12)(10+5x)(x-3)=0\) jest równa A.\((-5)\)
B.\((-1)\)
C.\(5\)
D.\(9\)
Właściciel restauracji kupił \(75\) kilogramów pomidorów: \(x\) kg pomidorów malinowych w cenie \(11\) złotych za kilogram oraz \(y\) kg pomidorów cherry w cenie \(7{,}98\) złotych za kilogram. Za pomidory zapłacił łącznie \(752{,}52\) złotych.
Oblicz, ile kilogramów pomidorów malinowych kupił właściciel restauracji. Zapisz obliczenia.
Funkcja \(f\) jest określona następująco: \[ f(x)= \begin{cases} -2x-10 & \text{dla } x\in(-5,-3],\\ x-1 & \text{dla } x\in(-3,4]. \end{cases} \] Wykres funkcji \(y=f(x)\) przedstawiono w kartezjańskim układzie współrzędnych \((x,y)\) na rysunku poniżej. 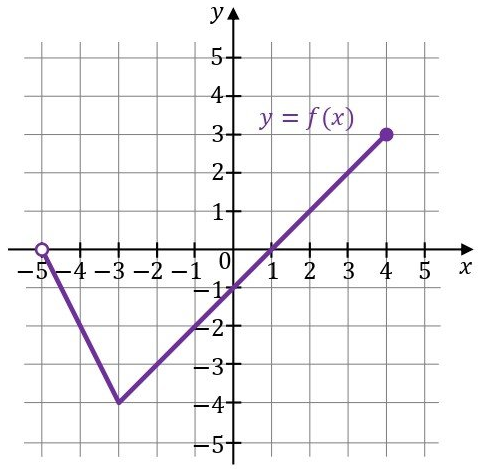

Uzupełnij zdania. Wpisz odpowiednie liczby w wykropkowanych miejscach, aby zdania były prawdziwe.
1. Miejscem zerowym funkcji \(f\) jest liczba ……… . 2. Wartość wyrażenia \(f(-2)+3\cdot f(2)\) jest równa ……… .
Uzupełnij zdania. Wpisz odpowiednie przedziały w wykropkowanych miejscach, aby zdania były prawdziwe.
1. Zbiorem wartości funkcji \(f\) jest przedział ………………… .2. Zbiorem wszystkich rozwiązań nierówności \(f(x)\lt -2\) jest przedział ………………… .
Miejscem zerowym funkcji liniowej \(g\) jest liczba \((-3)\). Dla argumentu \(0\) funkcja \(g\) przyjmuje wartość \(\left(-\frac{3}{2}\right)\).
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Funkcja \(g\) jest określona wzorem A.\(g(x)=-\tfrac{1}{2}\,x-\tfrac{3}{2}\)
B.\(g(x)=-\tfrac{1}{2}\,x+\tfrac{3}{2}\)
C.\(g(x)=\tfrac{1}{2}\,x-\tfrac{3}{2}\)
D.\(g(x)=\tfrac{1}{2}\,x+\tfrac{3}{2}\)
Funkcja kwadratowa \(f\) jest określona wzorem \(f(x)=\tfrac{1}{2}x^{2}+bx+c\), gdzie \(b\) oraz \(c\) są liczbami rzeczywistymi. Jednym z miejsc zerowych funkcji \(f\) jest liczba \(6\). W kartezjańskim układzie współrzędnych \((x,y)\) prosta o równaniu \(x=1\) jest osią symetrii wykresu funkcji \(f\).
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Funkcja \(f\) jest określona wzorem A.\(f(x)=\tfrac{1}{2}(x-4)(x-6)\)
B.\(f(x)=\tfrac{1}{2}(x-4)(x+6)\)
C.\(f(x)=\tfrac{1}{2}(x+4)(x-6)\)
D.\(f(x)=\tfrac{1}{2}(x+4)(x+6)\)
Oceń prawdziwość poniższych stwierdzeń. Wybierz P, jeśli stwierdzenie jest prawdziwe, albo F – jeśli jest fałszywe.
| Współczynnik \(b\) we wzorze funkcji \(f\) jest liczbą dodatnią. | P | F |
| Współczynnik \(c\) we wzorze funkcji \(f\) jest liczbą dodatnią. | P | F |
Funkcja \(g\) jest określona dla każdej liczby rzeczywistej \(x\) wzorem \(g(x)=f(x-3)\).
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Osią symetrii wykresu funkcji \(g\) jest prosta o równaniu A.\(x=-2\)
B.\(x=1\)
C.\(x=3\)
D.\(x=4\)
Ciąg \((a_{n})\) jest określony wzorem \(a_{n}=\frac{32\cdot(-1)^{n}}{2^{\,n-1}}\) dla każdej liczby naturalnej \(n\ge 1\).
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Szósty wyraz ciągu \((a_{n})\) jest równy A.\((-2)\)
B.\((-1)\)
C.\(1\)
D.\(2\)
Ciąg arytmetyczny \((a_{n})\) jest określony dla każdej liczby naturalnej \(n\ge 1\). Różnica tego ciągu jest równa \((-4)\) oraz \(a_{10}=-24\).
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Szósty wyraz ciągu \((a_{n})\) jest równy A.\((-12)\)
B.\((-8)\)
C.\((-4)\)
D.\(0\)
Ciąg geometryczny \((a_{n})\), o wszystkich wyrazach rzeczywistych różnych od \(0\), jest określony dla każdej liczby naturalnej \(n\ge 1\). Wyrazy tego ciągu spełniają warunek \(a_{3}=-8\cdot a_{6}\).
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Iloraz ciągu \((a_{n})\) jest równy A.\((-2)\)
B.\(\left(-\frac{1}{2}\right)\)
C.\(\frac{1}{2}\)
D.\(2\)
Trzywyrazowy ciąg \((\sqrt{5},\,1,\,x)\) jest arytmetyczny. Trzywyrazowy ciąg \((\sqrt{5},\,1,\,y)\) jest geometryczny.
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Liczby \(x\) oraz \(y\) spełniają warunki A.\(x<0\) i \(y<0\)
B.\(x<0\) i \(y>0\)
C.\(x>0\) i \(y<0\)
D.\(x>0\) i \(y>0\)
Kąt \(\alpha\) jest ostry oraz \(\cos\alpha=\frac{5}{13}\).
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Tangens kąta \(\alpha\) jest równy A.\(\frac{5}{12}\)
B.\(\frac{12}{13}\)
C.\(\frac{13}{12}\)
D.\(\frac{12}{5}\)
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Liczba \(\sin 30^\circ\cdot\cos 60^\circ+\sin 60^\circ\cdot\cos 30^\circ\) jest równa A.\(\frac{1}{2}\)
B.\(\frac{\sqrt{2}}{2}\)
C.\(\frac{\sqrt{3}}{2}\)
D.\(1\)
Punkty \(A\), \(B\), \(C\) oraz \(D\) leżą na okręgu o środku w punkcie \(S\) i o promieniu \(36\). Punkt \(S\) leży na odcinku \(BD\). Kąt \(BDA\) ma miarę \(40^\circ\), a kąt \(DBC\) ma miarę \(65^\circ\) (zobacz rysunek). 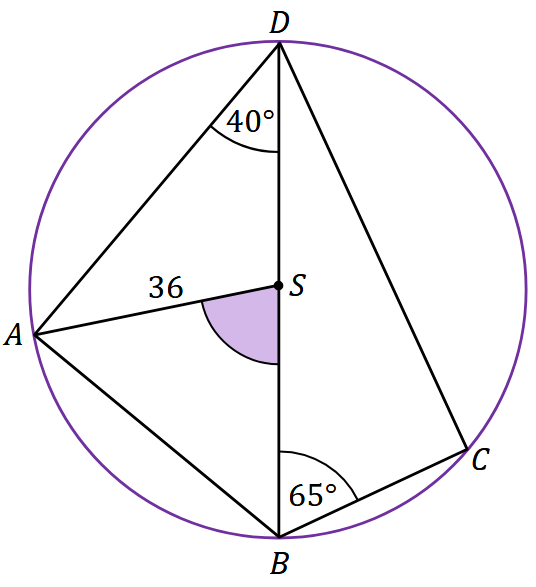

Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Miara kąta ostrego \(BSA\) jest równa A.\(20^\circ\)
B.\(40^\circ\)
C.\(50^\circ\)
D.\(80^\circ\)
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Długość łuku \(BC\), na którym jest oparty kąt wpisany \(CDB\), jest równa A.\(8\pi\)
B.\(10\pi\)
C.\(13\pi\)
D.\(20\pi\)
Dany jest trójkąt \(ABC\), w którym \(|AB|=6\), \(|AC|=4\) oraz \(|\angle CAB|=60^\circ\) (zobacz rysunek). 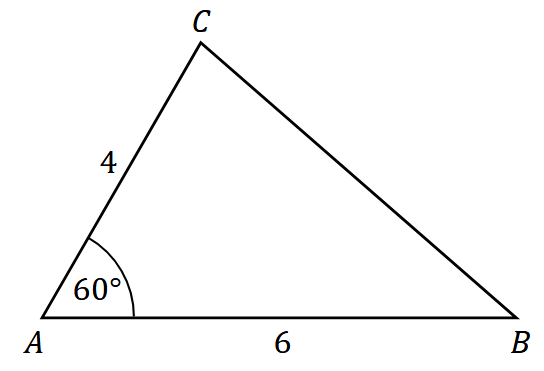

Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Pole trójkąta \(ABC\) jest równe A.\(6\)
B.\(6\sqrt{3}\)
C.\(12\)
D.\(12\sqrt{3}\)
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Długość boku \(BC\) trójkąta \(ABC\) jest równa A.\(\sqrt{28}\)
B.\(\sqrt{40}\)
C.\(8\)
D.\(\sqrt{76}\)
Dany jest trapez \(ABCD\) o podstawach \(AB\) i \(CD\) takich, że \(|AB|=2\cdot|CD|\). Przekątne \(AC\) i \(BD\) przecinają się w punkcie \(E\) (zobacz rysunek).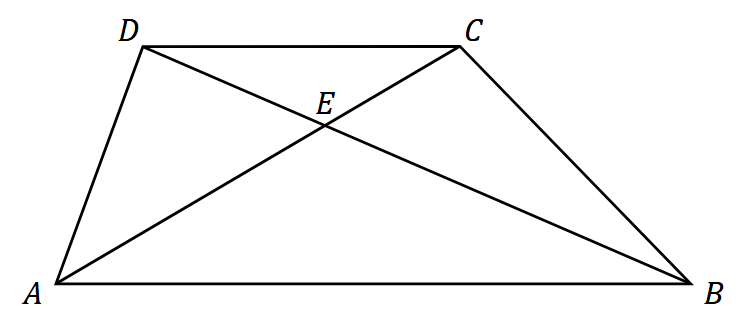

Oceń prawdziwość poniższych stwierdzeń. Wybierz P, jeśli stwierdzenie jest prawdziwe, albo F – jeśli jest fałszywe.
| Pola trójkątów \(BCE\) oraz \(AED\) są równe. | P | F |
| Pole trójkąta \(ABE\) jest dwa razy większe od pola trójkąta \(CDE\). | P | F |
W kartezjańskim układzie współrzędnych \((x, y)\) proste \(k\) oraz \(l\) są określone równaniami \[ k:\; y=(3-m)x+5 \qquad l:\; y=(m+3)x-4 \]
Uzupełnij zdanie. Wpisz odpowiednią liczbę w wykropkowanym miejscu, aby zdanie było prawdziwe.
Proste \(k\) oraz \(l\) są równoległe, gdy liczba \(m\) jest równa ........... .W kartezjańskim układzie współrzędnych \((x, y)\) dany jest okrąg \(\mathcal{O}\) o równaniu \[ \mathcal{O}:\ (x-1)^{2}+(y+3)^{2}=4 \]
Oceń prawdziwość poniższych stwierdzeń. Wybierz P, jeśli stwierdzenie jest prawdziwe, albo F – jeśli jest fałszywe.
| Okrąg \(\mathcal{O}\) nie ma punktów wspólnych z osią \(Ox\) układu współrzędnych. | P | F |
| Okrąg \(\mathcal{O}\) ma z osią \(Oy\) układu współrzędnych dokładnie dwa punkty wspólne. | P | F |
Dany jest graniastosłup prawidłowy trójkątny \(ABCDEF\). Wysokość podstawy \(ABC\) jest równa \(2\sqrt{3}\). Przekątna \(AE\) ściany bocznej \(ABED\) tworzy z krawędzią \(AB\) kąt o mierze \(60^\circ\) (zobacz rysunek). 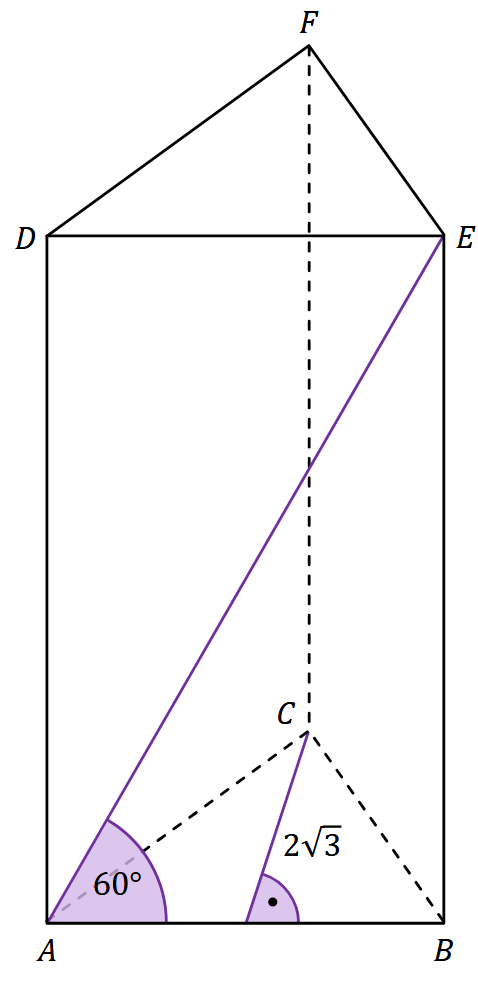

Oblicz objętość i pole powierzchni całkowitej tego graniastosłupa. Zapisz obliczenia.
Objętość walca o promieniu podstawy \(2\) jest równa \(16\pi^{2}\).
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Wysokość tego walca jest równa A.\(2\)
B.\(4\)
C.\(2\pi\)
D.\(4\pi\)
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Wszystkich trzycyfrowych liczb naturalnych większych od \(500\), w których zapisie dziesiętnym występują tylko cyfry nieparzyste, jest A.\(13\)
B.\(50\)
C.\(75\)
D.\(107\)
Doświadczenie losowe polega na dwukrotnym rzucie symetryczną sześcienną kostką do gry, która na każdej ściance ma inną liczbę oczek – od jednego oczka do sześciu oczek. Zapisujemy kolejno liczby wyrzuconych oczek i w ten sposób otrzymujemy liczbę dwucyfrową, przy czym pierwsza wyrzucona liczba oczek jest cyfrą dziesiątek, a druga – cyfrą jedności tej liczby dwucyfrowej.
Oblicz prawdopodobieństwo zdarzenia \(A\) polegającego na tym, że otrzymana w ten sposób liczba dwucyfrowa będzie nieparzysta i podzielna przez \(3\). Zapisz obliczenia.
W stacji diagnostycznej odnotowywano liczby usterek wykrytych podczas przeglądów technicznych pięcioletnich samochodów w lipcu \(2025\) roku. 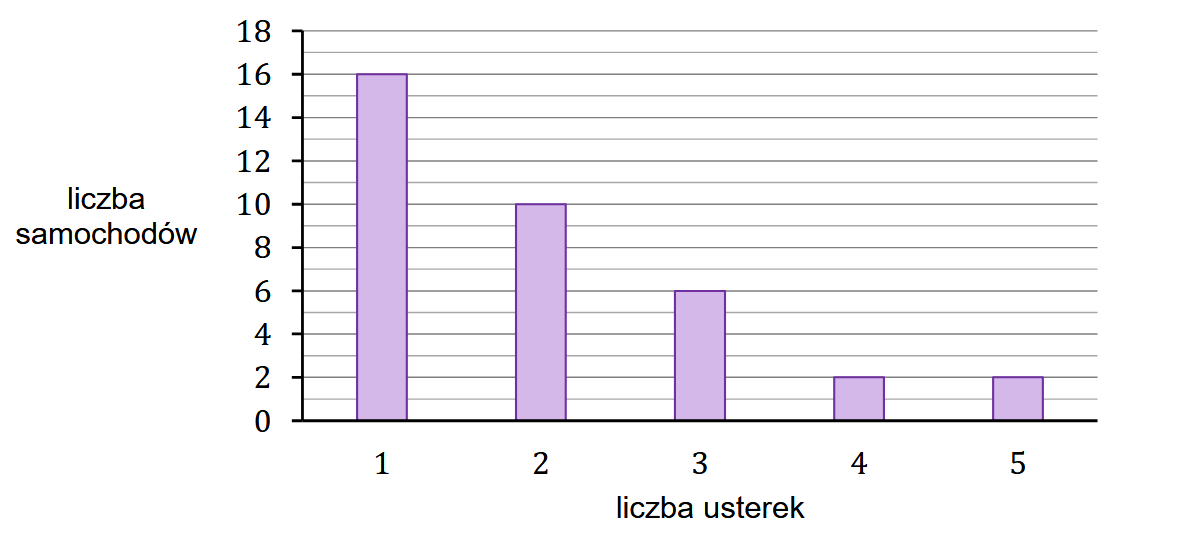
Wszystkie odnotowane wyniki przedstawiono na poniższym diagramie.
Na osi poziomej podano liczbę usterek, które zostały wykryte podczas przeglądów, a na osi pionowej podano liczbę samochodów, w których wykryto daną liczbę usterek.
Uzupełnij zdania. Wpisz odpowiednie liczby w wykropkowanych miejscach, aby zdania były prawdziwe.
- Dominanta liczby usterek wykrytych na tej stacji podczas tych przeglądów jest równa ........ .
- Średnia arytmetyczna liczby usterek wykrytych na tej stacji podczas tych przeglądów jest równa ........ .
- Liczba samochodów, w których wykryto podczas tych przeglądów co najmniej dwie usterki, stanowi ........ procent liczby samochodów, w których wykryto dokładnie jedną usterkę.
Hotel ma do dyspozycji gości \(80\) pokoi jednoosobowych. Właściciel hotelu przeanalizował wpływ ceny za dobę hotelową na liczbę wynajętych pokoi i stwierdził, że:
- przy wyjściowej cenie wynoszącej \(120\) zł za jedną dobę hotelową wszystkie pokoje są wynajęte
- każdy wzrost ceny za dobę hotelową o \(5\) zł skutkuje spadkiem liczby wynajmowanych pokoi o \(1\).
Oblicz, jaka powinna być cena wynajęcia jednoosobowego pokoju (za dobę hotelową), aby dobowy przychód hotelu z wynajmowania pokoi był największy. Zapisz obliczenia.