Kula

Drukuj

Poziom podstawowy

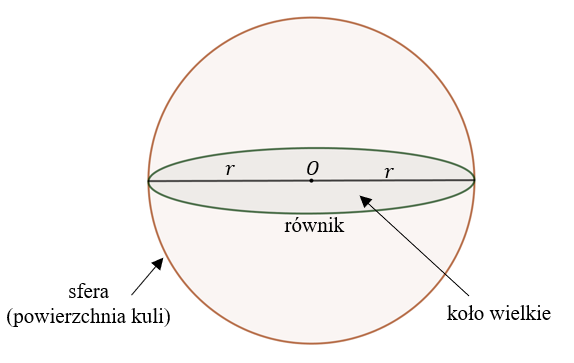
Kula - to bryła obrotowa, powstała przez obrót koła wokół jego średnicy.
Powierzchnię kuli nazywamy sferą.
Przekrój kuli jest kołem. Jeżeli płaszczyzna przekroju przechodzi przez środek kuli, to taki przekrój nazywamy kołem wielkim.

Wzór na pole kuli: \[P=4\pi r^2\] Wzór na objętość kuli: \[V=\frac{4}{3}\pi r^3\] gdzie \(r\) - to promień kuli.

Kula ma objętość \(V = 288\pi\). Promień \(r\) tej kuli jest równy

A.\( 6 \)

B.\( 8 \)

C.\( 9 \)

D.\( 12 \)

Objętość kuli o promieniu \( \;r=\pi\;\text{dm}\; \) jest równa

A.\(\frac{4}{3}\pi\;\text{dm}^3 \)

B.\(\frac{4}{3}\pi^4\;\text{dm}^3 \)

C.\(\frac{3}{4}\pi^4\;\text{dm}^3 \)

D.\(\frac{3}{4}\pi^3\;\text{dm}^3 \)

Kula o promieniu \(5\) cm i stożek o promieniu podstawy \(10\) cm mają równe objętości. Wysokość stożka jest równa

A.\( \frac{25}{\pi } \) cm

B.\( 10 \) cm

C.\( \frac{10}{\pi } \) cm

D.\( 5 \) cm

Przedstawiona na rysunku bryła składa się z walca i półkuli. Wysokość walca jest taka, jak promień jego podstawy i jest równa \(R\).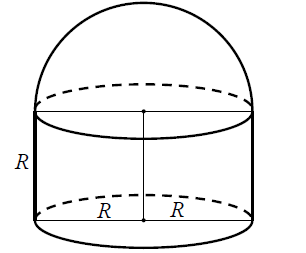

Objętość tej bryły jest równa

A.\( \pi R^3 \)

B.\( \frac{5}{3}\pi R^3 \)

C.\( \frac{2}{3}\pi R^3 \)

D.\( 2\pi R^3 \)

Stożek o promieniu podstawy \(r\) i kula o tym samym promieniu mają równe objętości. Tangens kąta między tworzącą i płaszczyzną podstawy tego stożka jest równy

A.\( \frac{4}{3} \)

B.\( 12 \)

C.\( \sqrt{17} \)

D.\( 4 \)

Kula o promieniu \(6\) cm i walec o wysokości równej \(4{,}5\) cm mają równe objętości. Średnica podstawy walca ma długość:

A.\( 8 \) cm

B.\( 8\sqrt{2} \) cm

C.\( 16 \) cm

D.\( 20 \) cm

Promień kuli i promień podstawy stożka są równe \(4\). Pole powierzchni kuli jest równe polu powierzchni całkowitej stożka. Długość tworzącej stożka jest równa

A.\( 8 \)

B.\( 4 \)

C.\( 16 \)

D.\( 12 \)

Pole powierzchni całkowitej pewnego stożka jest \(3\) razy większe od pola powierzchni pewnej kuli. Promień tej kuli jest równy \(2\) i jest taki sam jak promień podstawy tego stożka. Tworząca tego stożka ma długość równą

A.\( 12 \)

B.\( 11 \)

C.\( 24 \)

D.\( 22 \)

Rio de Janeiro leży na \(23\) stopniu szerokości geograficznej południowej. Jaką drogę pokona Jose w wyniku ruchu obrotowego Ziemi dookoła własnej osi podczas lekcji portugalskiego? Przyjmij, że średnica Ziemi wynosi \(12600\ \text{km}\).

W kulę o promieniu \(5\) wpisano stożek o kącie rozwarcia \(90^\circ \). Oblicz pole powierzchni całkowitej stożka.

\(P=25\pi (1+\sqrt{2})\)

Metalowy stożek, którego tworząca o długości \(10\) jest nachylona do płaszczyzny podstawy pod kątem \(30^\circ \), przetopiono na sześć jednakowych kulek. Oblicz promień kulki.

\(r=\frac{5}{2}\)