Interpretacja geometryczna wartości bezwzględnej

Drukuj

Poziom podstawowy

Wskaż rysunek, na którym jest przedstawiony zbiór rozwiązań nierówności \(|x-2| \ge 3\).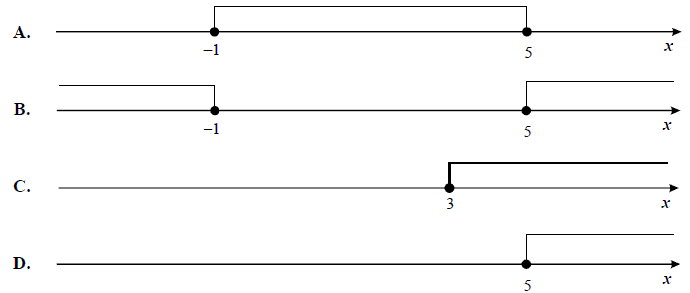

Wskaż rysunek, na którym zaznaczony jest zbiór wszystkich liczb rzeczywistych spełniających nierówność \(|x + 4| \lt 5\)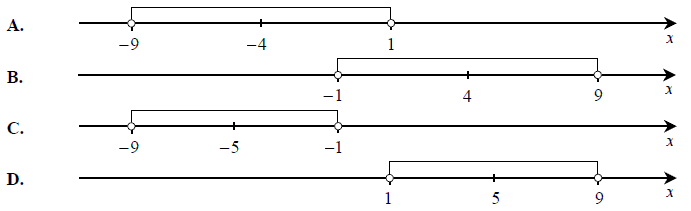

Zbiór rozwiązań nierówności \(|x-3|\le 2\) przedstawiony jest na rysunku: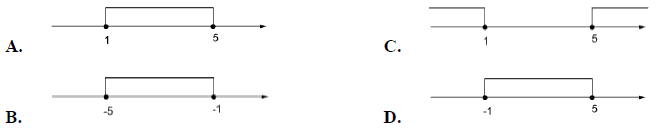

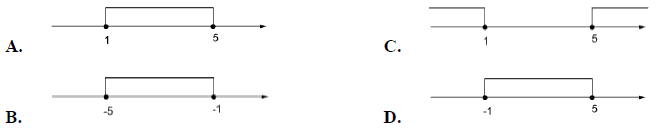
Zbiór rozwiązań nierówności \(|x+3|>4\) jest przedstawiony na rysunku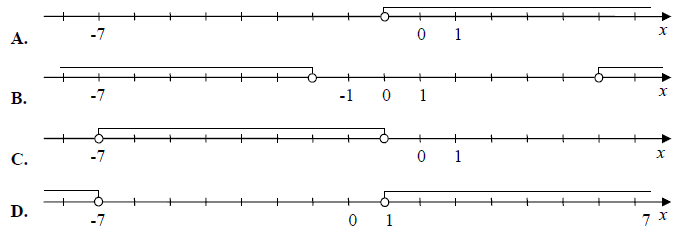

Zbiór rozwiązań nierówności \(|x - 3| \ge 1\) jest przedstawiony na rysunku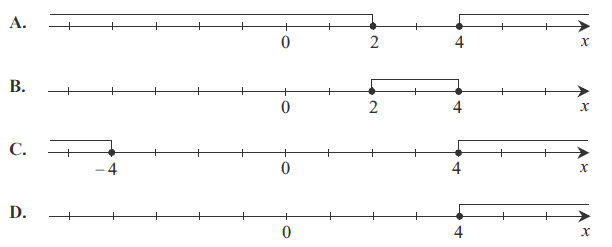

Który z zaznaczonych przedziałów jest zbiorem rozwiązań nierówności \(|2 - x| \le 3\).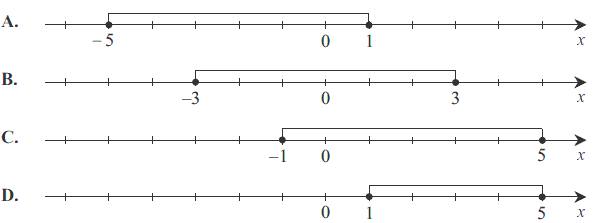

Zaznacz na osi liczbowej punkty opisane równością \(|x + 1|=4\).

Zaznacz na osi liczbowej przedział opisany nierównością \(|x + 1| \le 4\).

Wskaż nierówność, która opisuje przedział zaznaczony na osi liczbowej.

A.\(|x-7|\lt 15 \)

B.\(|x-7|>15 \)

C.\(|x-15|\lt 7 \)

D.\(|x-15|>7 \)

Przedział \(\langle -1,3 \rangle\) jest opisany nierównością

A.\( |x+1|\ge 2 \)

B.\( |x+1|\le 2 \)

C.\( |x-1|\le 2 \)

D.\( |x-1|\ge 2 \)

Wskaż rysunek na którym przedstawiono przedział, będący zbiorem wszystkich rozwiązań nierówności \(-4\le x-1\le 4\).

C (na filmiku D)

Na rysunku przedstawiony jest zbiór wszystkich liczb rzeczywistych spełniających nierówność \(|2x-8|\le 10\).

Wynika stąd, że

A.\( k=2 \)

B.\( k=4 \)

C.\( k=5 \)

D.\( k=9 \)