Egzamin ósmoklasisty 2025 maj
Szkoła podstawowa
Deskorolka kosztuje \(180\) zł. Na diagramie przedstawiono kwoty, które Aldona odłożyła w styczniu, w lutym, w marcu i w kwietniu na zakup deskorolki. 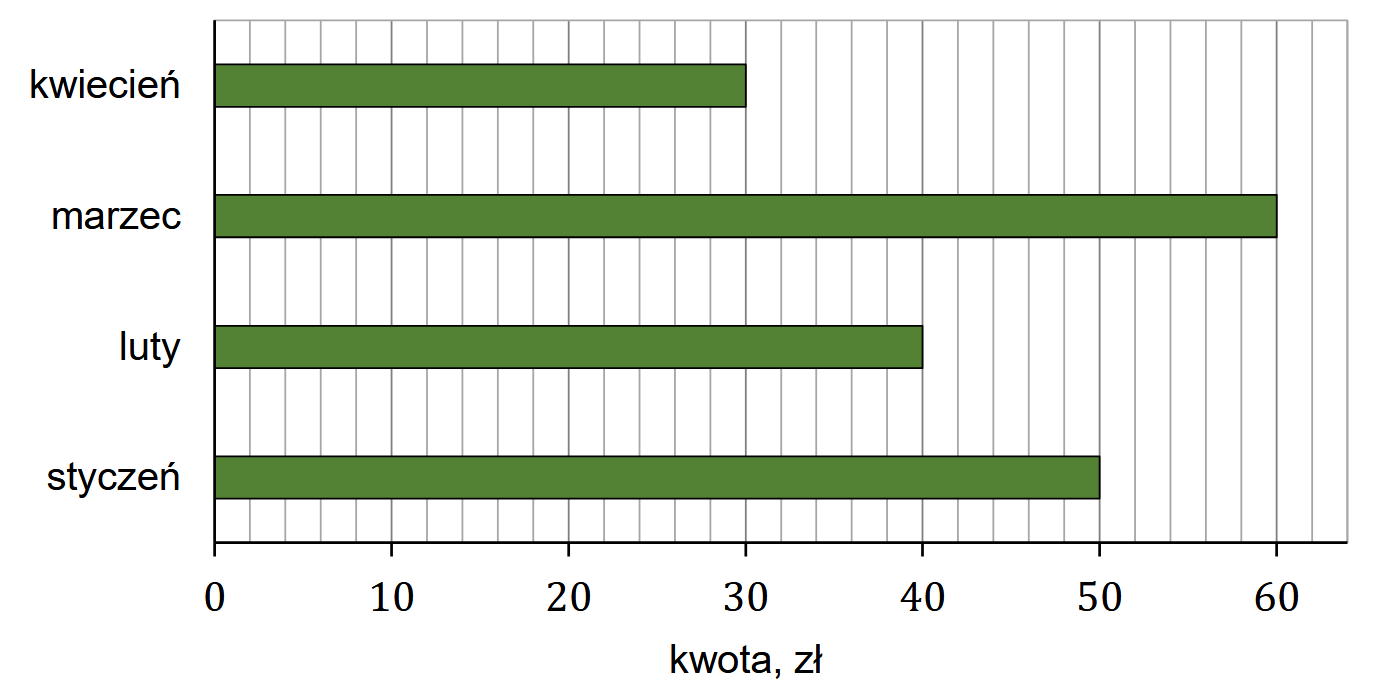 W marcu Aldona odłożyła kwotę o
W marcu Aldona odłożyła kwotę o

Uzupełnij zdania. Wybierz odpowiedź spośród oznaczonych literami A i B oraz odpowiedź spośród oznaczonych literami C i D.
W styczniu i lutym łącznie Aldona odłożyła A
B
kwoty potrzebnej na zakup deskorolki. A.\(45 \%\)
B.\(50 \%\)
C
D
większą od kwoty odłożonej w styczniu. C.\(10 \%\)
D.\(20 \%\)
Dane jest wyrażenie \[ \left(2,4-5\frac{1}{3}\right):(-2) \]
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Wartość tego wyrażenia jest równa A.\(\left(-1\frac{8}{15}\right)\)
B.\(\left(-1\frac{7}{15}\right)\)
C.\(1\frac{7}{15}\)
D.\(1\frac{8}{15}\)
Dane są liczby: 91, 92, 95, 97.
Która z podanych liczb przy dzieleniu przez 7 daje resztę 1? Wybierz właściwą odpowiedź spośród podanych.
A. 91
B. 92
C. 95
D. 97
Średnia arytmetyczna czterech liczb \(a, b, c, d\) jest równa \(9\), a średnia arytmetyczna dwóch liczb \(e\) i \(f\) jest równa \(6\). Średnia arytmetyczna liczb \(a, b, c, d, e, f\) jest równa
Uzupełnij zdania. Wybierz odpowiedź spośród oznaczonych literami A i B oraz odpowiedź spośród oznaczonych literami C i D.
Suma liczb \(a, b, c, d\) jest o A
B
większa od sumy liczb \(e\) i \(f\). A.\(3\)
B.\(24\)
C
D
. C.\(8\)
D.\(7{,}5\)
Obwód pięciokąta przedstawionego na rysunku wyraża się wzorem \(L = 2a + 2b + c\). 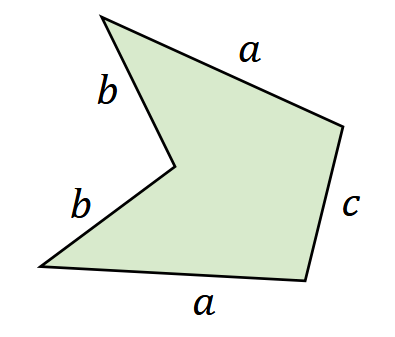

Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Wielkość \(a\) wyznaczoną poprawnie z podanego wzoru opisuje równanie A.\(a = \dfrac{L-2b-c}{2}\)
B.\(a = \dfrac{L-2b+c}{2}\)
C.\(a = L + 2b - c\)
D.\(a = L - 2b - c\)
W pudełku znajdują się wyłącznie piłki białe, fioletowe i czarne. Piłek białych jest \(4\) razy więcej niż fioletowych i o \(3\) mniej niż czarnych. Liczbę piłek fioletowych oznaczymy przez \(x\).
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Łączną liczbę wszystkich piłek w pudełku opisuje wyrażenie A.\(9x+3\)
B.\(9x-3\)
C.\(6x+3\)
D.\(6x-3\)
Dane są wyrażenia: \[ K=\frac{1}{9}\cdot\sqrt{\frac{1}{16}}-\frac{1}{16}\cdot\sqrt{\frac{1}{9}}, \qquad L=9\cdot\sqrt{16}-16\cdot\sqrt{9}. \] Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, albo F – jeśli jest fałszywe.
| Wyrażenie \(K\) ma wartość ujemną. | P | F |
| Wartość wyrażenia \(L\) jest większa od wartości wyrażenia \(K\). | P | F |
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Wartość wyrażenia \(8^{6}:4^{3}\) zapisana w postaci potęgi liczby 2 jest równa A.\(2^{2}\)
B.\(2^{3}\)
C.\(2^{4}\)
D.\(2^{12}\)
Rowerzysta pokonał odcinek drogi o długości \(100\;\text{m}\) z prędkością \(5\;\dfrac{\text{m}}{\text{s}}\).
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Rowerzysta pokonał ten odcinek drogi w czasie A. \(50\) sekund
B. \(20\) sekund
C. \(500\) sekund
D. \(200\) sekund
Na loterię przygotowano \(72\) losy i ponumerowano je kolejnymi liczbami naturalnymi od \(1\) do \(72\). Wygrywają losy o numerach od \(1\) do \(9\) oraz od \(46\) do \(72\). Pozostałe losy są puste. Ada jako pierwsza wyciąga jeden los.
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Prawdopodobieństwo wyciągnięcia przez Adę losu pustego jest równe A.\(\dfrac{26}{72}\)
B.\(\dfrac{27}{72}\)
C.\(\dfrac{35}{72}\)
D.\(\dfrac{36}{72}\)
Dany jest trójkąt prostokątny \(A B C\). Na środku boku \(A B\) zaznaczono punkt \(D\). Następnie poprowadzono odcinek \(D C\), dzielący trójkąt \(A B C\) na dwa trójkąty \(A D C\) i \(D B C\). Ponadto \(|A D|=|D B|=30 \mathrm{~cm}\) oraz \(|D C|=50 \mathrm{~cm}\) (zobacz rysunek). 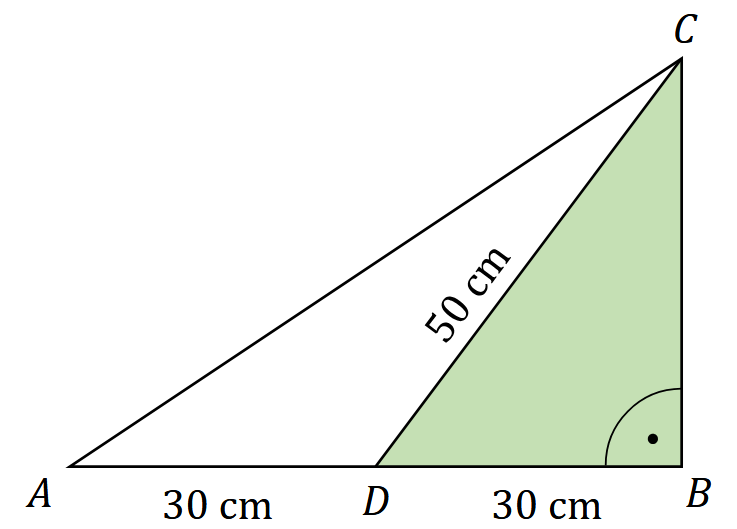

Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, albo F – jeśli jest fałszywe.
| Pole trójkąta \(DBC\) jest równe \(600\;\mathrm{cm}^{2}\). | P | F |
| Pole trójkąta \(ABC\) jest dwa razy większe od pola trójkąta \(ADC\). | P | F |
Na osi liczbowej zaznaczono punkty \(A\), \(B\) i \(C\). Odcinek \(AC\) jest podzielony na \(6\) równych części. 

Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, albo F – jeśli jest fałszywe.
| Współrzędna punktu \(C\) jest liczbą parzystą. | P | F |
| Współrzędna punktu \(B\) jest liczbą mniejszą od \(74\). | P | F |
Trapez \(ABCD\) podzielono na trzy figury: kwadrat \(AEGD\), trójkąt \(EFG\) i romb \(FBCG\) (zobacz rysunek). Na rysunku podano również długości boków trójkąta \(EFG\). 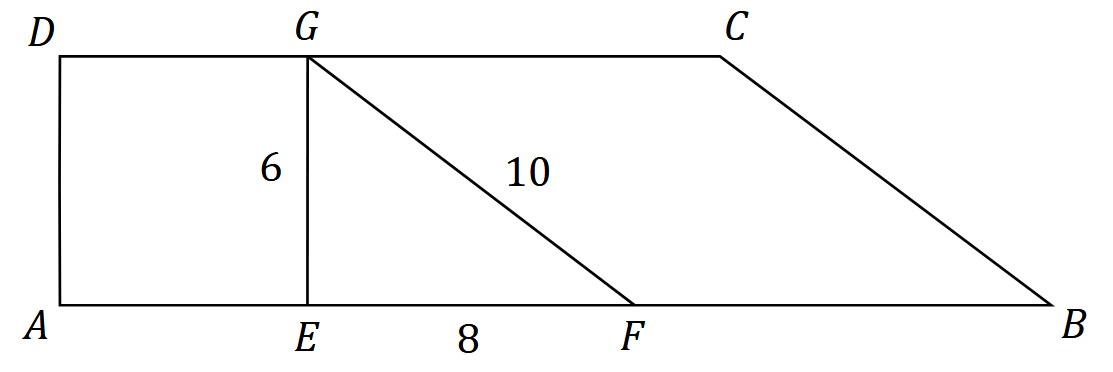

Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Obwód trapezu \(ABCD\) jest równy A.\(56\)
B.\(72\)
C.\(88\)
D.\(120\)
W układzie współrzędnych \((x, y)\) zaznaczono trzy punkty, które są wierzchołkami równoległoboku \(ABCD\): \(A=(-3,-2)\), \(C=(4,2)\), \(D=(-1,2)\) (zobacz rysunek). 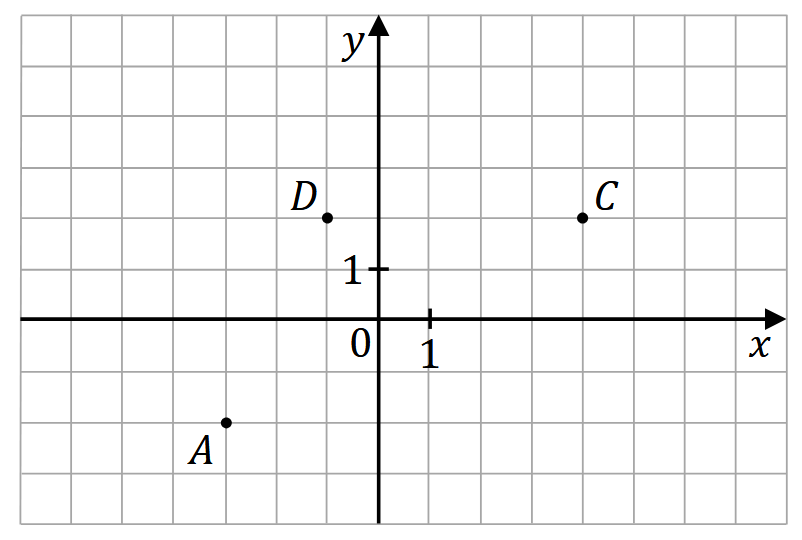 Współrzędna \(x\) wierzchołka \(B\), niezaznaczonego na rysunku, jest liczbą dodatnią.
Współrzędna \(x\) wierzchołka \(B\), niezaznaczonego na rysunku, jest liczbą dodatnią.
 Współrzędna \(x\) wierzchołka \(B\), niezaznaczonego na rysunku, jest liczbą dodatnią.
Współrzędna \(x\) wierzchołka \(B\), niezaznaczonego na rysunku, jest liczbą dodatnią. Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Niezaznaczony na rysunku wierzchołek \(B\) tego równoległoboku ma współrzędne A.\((4,-2)\)
B.\((3,-2)\)
C.\((2,-2)\)
D.\((6,-2)\)
Trzy krawędzie wychodzące z jednego wierzchołka prostopadłościanu mają długości: \(5\), \(6\), \(7\) (zobacz rysunek). 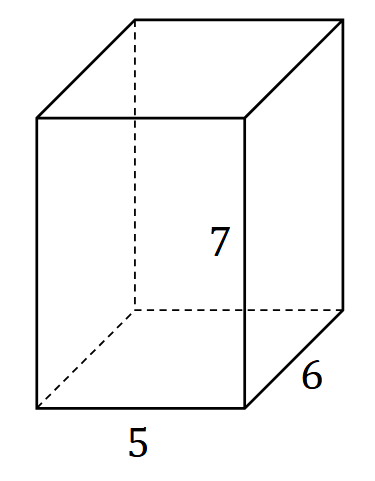

Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Pole powierzchni całkowitej tego prostopadłościanu jest równe A.\(107\)
B.\(172\)
C.\(210\)
D.\(214\)
Liczbę \(\frac{7}{15}\) zapisano w postaci sumy trzech ułamków zwykłych, z których jeden jest równy \(\frac{1}{5}\), a drugi \(\frac{1}{6}\).
Uzasadnij, że trzeci składnik tej sumy można przedstawić w postaci ułamka zwykłego, którego licznik jest równy 1, a mianownik jest liczbą całkowitą dodatnią. Zapisz obliczenia.
Troje przyjaciół - Andrzej, Basia i Marek - zbiera plakaty. Andrzej ma o \(28\) plakatów więcej od Basi, a Marek ma ich \(3\) razy mniej od Basi. Andrzej i Marek mają razem \(2\) razy więcej plakatów od Basi.
Oblicz, ile plakatów ma każde z tych przyjaciół. Zapisz obliczenia.
Na rysunku przedstawiono trapez \(ABCD\), w którym kąt \(ABC\) ma miarę \(48^{\circ}\). Odcinek \(EC\) dzieli ten trapez na równoległobok \(AECD\) i trójkąt \(EBC\), w którym kąt \( BCE \) ma miarę \(57^{\circ}\) (zobacz rysunek). 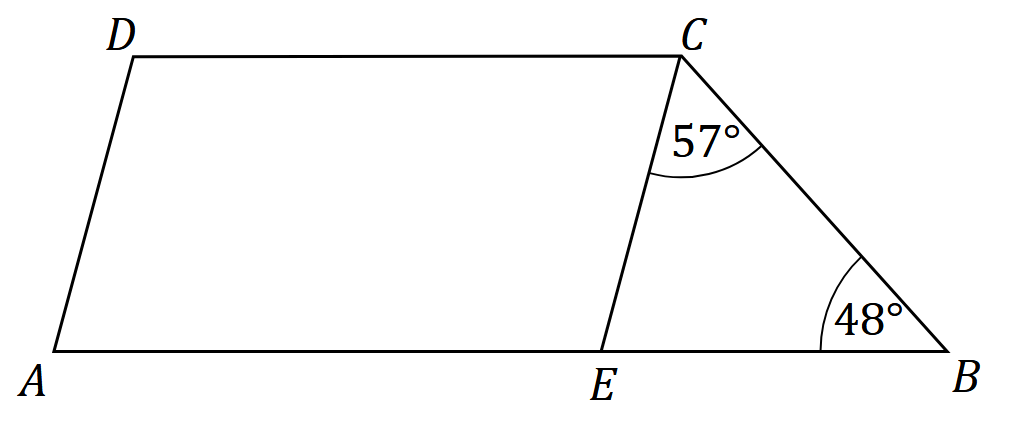

Oblicz miary kątów \(DAB\), \(BCD\) oraz \(CDA\) trapezu \(ABCD\). Zapisz obliczenia.
Na ścianie wiszą dwie tablice: mała kwadratowa i duża prostokątna. Mała tablica narysowana w skali \(1:20\) jest kwadratem o boku \(3\) cm . Rzeczywiste wymiary dużej prostokątnej tablicy są równe \(240\) cm i \(90\) cm .
Oblicz, ile razy pole dużej tablicy jest większe od pola małej tablicy. Zapisz obliczenia.
Dany jest kwadrat \(ABCD\) o boku długości \(15\ \text{cm}\). Każdy z boków \(AB\) i \(CD\) podzielono na trzy równe części, a każdy z boków \(AD\) i \(BC\) podzielono na pięć równych części. Na boku \(BC\) zaznaczono punkt \(E\), na boku \(CD\) zaznaczono punkt \(F\), a ponadto poprowadzono odcinki \(AE\) i \(AF\) (zobacz rysunek). 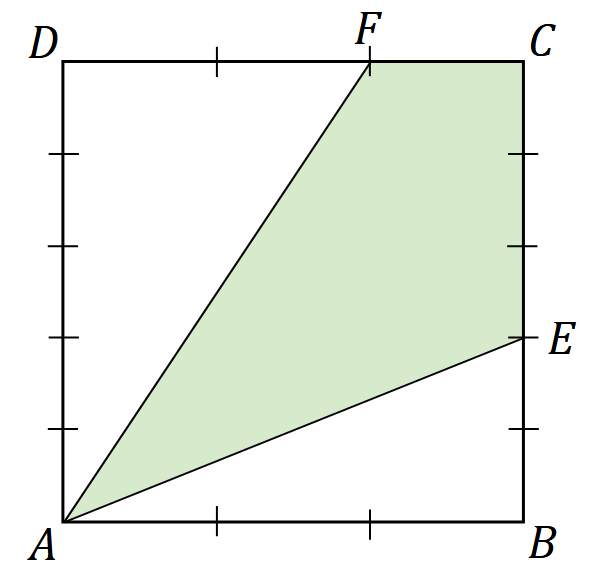

Oblicz pole czworokąta \(AECF\). Zapisz obliczenia.
Dany jest ostrosłup prawidłowy czworokątny, w którym wysokość ściany bocznej poprowadzona do krawędzi podstawy jest równa \(12\ \text{cm}\) (zobacz rysunek). 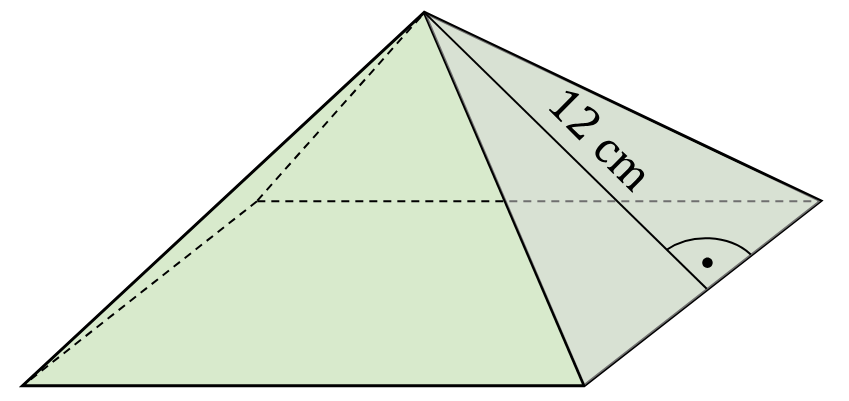 Pole powierzchni jednej ściany bocznej tego ostrosłupa jest równe \(108\ \text{cm}^2\).
Pole powierzchni jednej ściany bocznej tego ostrosłupa jest równe \(108\ \text{cm}^2\).
 Pole powierzchni jednej ściany bocznej tego ostrosłupa jest równe \(108\ \text{cm}^2\).
Pole powierzchni jednej ściany bocznej tego ostrosłupa jest równe \(108\ \text{cm}^2\). Oblicz sumę długości wszystkich krawędzi tego ostrosłupa. Zapisz obliczenia.
Tematy nadrzędne i sąsiednie