Czworokąt wpisany w okrąg

Drukuj

Poziom rozszerzony

Czworokąt można wpisać w okrąg, jeżeli sumy jego przeciwległych kątów wewnętrznych są równe, czyli gdy zachodzi warunek: \[\alpha +\gamma =\beta +\delta=180^\circ \] Wówczas środek okręgu pisanego na czworokącie leży na przecięciu symetralnych boków: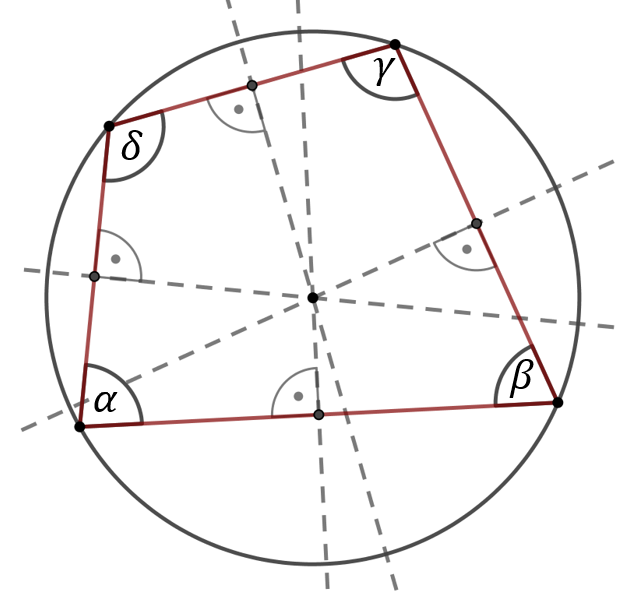

Pole czworokąta wpisanego w okrąg można obliczyć ze wzoru Brahmagupty: \[P=\sqrt{(p-a)(p-b)(p-c)(p-d)}\] gdzie \(p\) - to połowa obwodu czworokąta, czyli: \(p=\frac{a+b+c+d}{2}\).

W tym filmiku omawiam własności czworokątów wpisanych w okrąg i opisanych na okręgu.

Czas nagrania: 7 min.

W trapezie \(A B C D\) o podstawach \(A B\) i \(C D\), w którym \(|A B|\gt |C D|\) oraz \(|A B|+|C D|\gt|A D|+|B C|\) poprowadzono dwusieczne kątów wewnętrznych. Dwusieczne kątów \(A\) i \(D\) przecinają się w punkcie \(K\), a dwusieczne kątów \(B\) i \(C\) w punkcie \(L\). Wykaż, że \(2|K L|=|A B|+|C D|-|A D|-|B C|\).