Czworokąt opisany na okręgu
Poziom rozszerzony
Okrąg można wpisać w czworokąt wtedy i tylko wtedy, gdy sumy długości przeciwległych boków tego czworokąta są równe: \[|AB|+|CD|=|AD|+|BC|\] Wówczas środek okręgu wpisanego leży w punkcie przecięcia dwusiecznych kątów wewnętrznych. 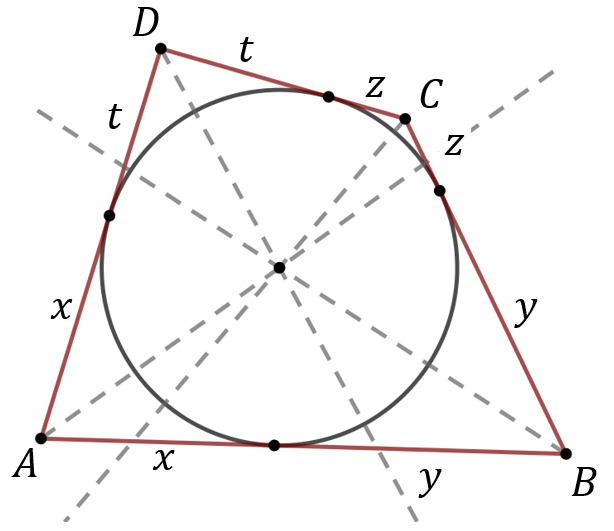 Warunek na wpisanie okręgu w czworokąt wynika z równości odcinków stycznych: \[ |AB|+|CD|=|AD|+|BC|\\[6pt] (x+y)+(z+t)=(x+t)+(y+z) \] Wzór na pole czworokąta opisanego na okręgu o promieniu \(r\): \[ P=\frac{1}{2}(|AB|+|BC|+|CD|+|DA|) \cdot r \] Powyższy wzór to jest po prostu suma pól czterech trójkątów:
Warunek na wpisanie okręgu w czworokąt wynika z równości odcinków stycznych: \[ |AB|+|CD|=|AD|+|BC|\\[6pt] (x+y)+(z+t)=(x+t)+(y+z) \] Wzór na pole czworokąta opisanego na okręgu o promieniu \(r\): \[ P=\frac{1}{2}(|AB|+|BC|+|CD|+|DA|) \cdot r \] Powyższy wzór to jest po prostu suma pól czterech trójkątów: 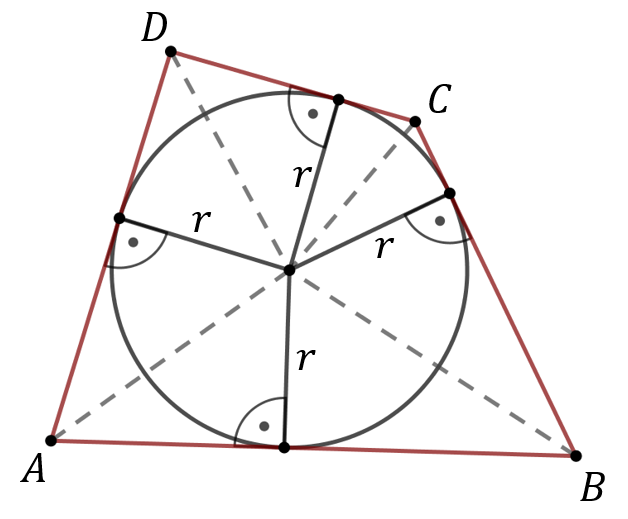 \[ \begin{gathered} P=\frac{1}{2}|A B| \cdot r+\frac{1}{2}|B C| \cdot r+\frac{1}{2}|C D| \cdot r+\frac{1}{2}|D A| \cdot r= \\ =\frac{1}{2}(|A B|+|B C|+|C D|+|D A|) \cdot r \end{gathered} \]
\[ \begin{gathered} P=\frac{1}{2}|A B| \cdot r+\frac{1}{2}|B C| \cdot r+\frac{1}{2}|C D| \cdot r+\frac{1}{2}|D A| \cdot r= \\ =\frac{1}{2}(|A B|+|B C|+|C D|+|D A|) \cdot r \end{gathered} \] Pole czworokąta opisanego i wpisanego w okrąg
Jeżeli czworokąt o bokach długości \(a,b,c,d\) jest jednocześnie wpisany w okrąg i opisany na na okręgu, to jego pole można obliczyć ze wzoru: \[ P=\sqrt{a b c d} \] Wynika to z tego, że wówczas wzór Brahmagupty na pole czworokąta wpisanego w okrąg: \[P=\sqrt{(p-a)(p-b)(p-c)(p-d)}\] gdzie: \(p=\frac{a+b+c+d}{2}\) można uprościć korzystając z własności czworokąta opisanego na okręgu: \[a+c=b+d\]W tym filmiku omawiam własności czworokątów wpisanych w okrąg i opisanych na okręgu.
Czas lekcji: 7 min.
W trapezie \(A B C D\), \(AB \parallel DC\), suma kątów \(B A D\) i \(C B A\) jest równa \(90^{\circ}\). W trapez wpisano okrąg o środku w punkcie \(O\) i promieniu \(1\). Odcinek \(AB\) ma długość \(5\). Oblicz \(|CD|\).
Dany jest trapez o podstawach \(a\) i \(b\) opisany na okręgu o promieniu \(r\). Wykaż, że \(4r^2 \leq ab\). 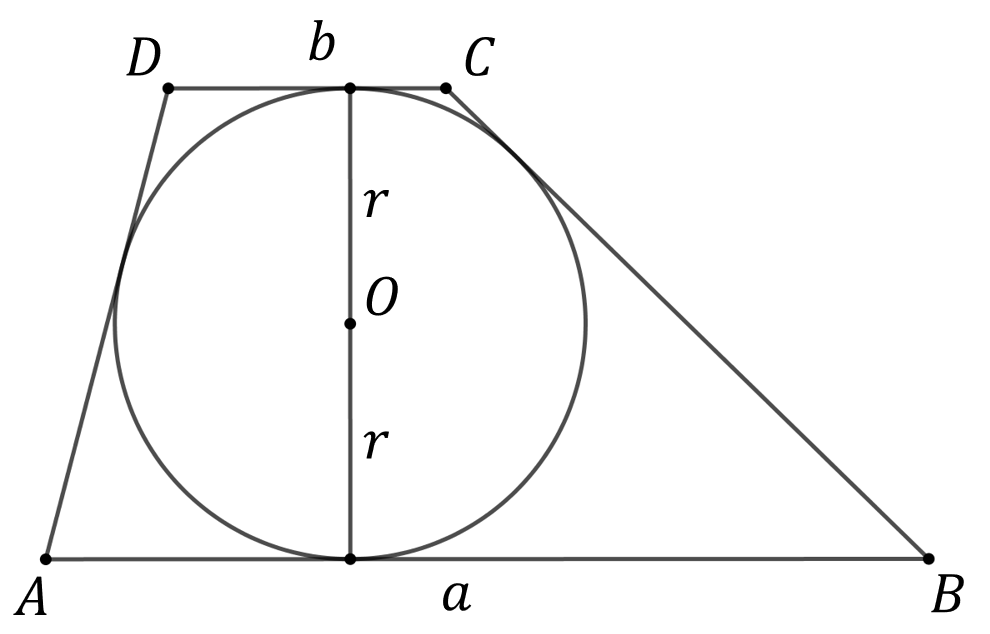

Tematy nadrzędne i sąsiednie