Matura podstawowa - kurs - część 30 - zadania

Wykres funkcji \(f(x)=x^2-2x-8,\) gdzie \(x \in \mathbb{R}\), przecina oś \(OX\) w punktach \(A\) i \(B\).

• Wyznacz współrzędne punktów \(A\) i \(B\).
• Oblicz pole trójkąta \(AWB\), jeśli \(W\) jest wierzchołkiem paraboli będącej wykresem funkcji \(f\).

Funkcja kwadratowa \(f\) określona jest wzorem \(f(x) = ax^2 + bx + c\). Zbiorem rozwiązań nierówności \(f(x) \gt 0\) jest przedział \((0,12)\). Największa wartość funkcji \(f\) jest równa \(9\). Oblicz współczynniki \(a\), \(b\) i \(c\) funkcji \(f\).

Rozważmy prostokąt o polu mniejszym od \(24\), w którym jeden bok jest od drugiego dłuższy o \(5\). Oblicz długość dłuższego boku prostokąta, jeśli jest ona liczbą całkowitą parzystą.

Do napełniania basenu służą dwie pompy. Pierwsza z nich ma wydajność o \(20\%\) większą niż druga. Napełnienie pustego basenu tylko drugą pompą trwa o \(1\) godzinę i \(40\) minut dłużej niż przy użyciu tylko pierwszej pompy. Oblicz, jaką część pustego basenu napełnią w ciągu jednej godziny obie pompy, pracując jednocześnie.

Na rysunku przedstawiony jest fragment wykresu funkcji kwadratowej \(f\). Osią symetrii paraboli jest prosta o równaniu \(x=-3\). Rozwiązaniem nierówności \(f(x)\le 0\) jest zbiór

Wyznacz wzór funkcji kwadratowej \(f\) w postaci ogólnej, wiedząc, że zbiorem wartości tej funkcji jest przedział \((-\infty ,-1\rangle \), a wartość \(-5\) osiąga ona dla dwóch argumentów: \(2\) i \(10\).

Na rysunku są przedstawione fragmenty wykresów funkcji kwadratowych \(f\) i \(g\). Funkcja \(f\) jest określona wzorem \(f(x)=-x^2+6x-5\), a mniejsze z jej miejsc zerowych jest jednocześnie miejscem zerowym funkcji \(g\). Wierzchołek \(W\) paraboli, która jest wykresem funkcji \(f\), leży na wykresie funkcji \(g\), a wierzchołek \(Z\) paraboli będącej wykresem funkcji \(g\) leży na osi \(Oy\) układu współrzędnych. Wyznacz wzór funkcji \(g\).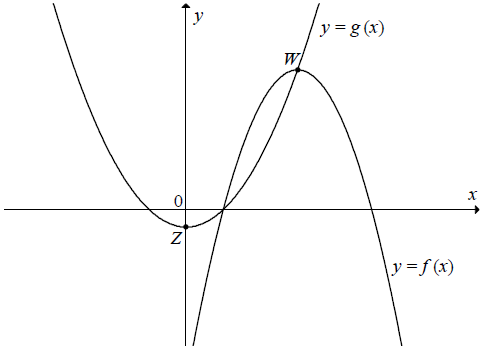

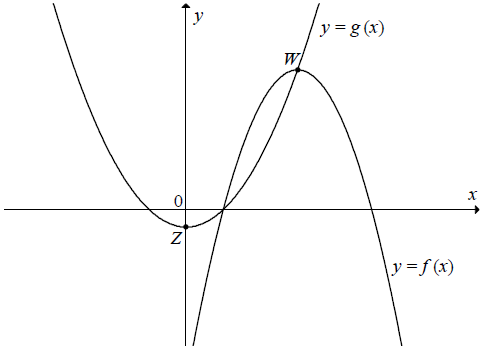
Wykres funkcji kwadratowej \(f\) przecina oś \(Ox\) w punktach \(x=1\) oraz \(x=3\) i przechodzi przez punkt \((0,-3)\). Wykres ten przesunięto i otrzymano wykres funkcji kwadratowej \(g(x)=f(x-p)\). Wierzchołek funkcji \(g\) leży na osi \(Oy\). Wyznacz wzór funkcji \(g\).

Parabola, która jest wykresem funkcji kwadratowej \(f(x)=ax^2+bx+c\), przechodzi przez punkt \((-2,10)\) oraz \(f(-1)=f(3)=0\). Oblicz odległość wierzchołka paraboli od początku układu współrzędnych.

Funkcja kwadratowa \(f\), której miejscami zerowymi są liczby \(-2\) i \(4\), dla argumentu \(1\) przyjmuje wartość \(3\). Uzasadnij, że wykres funkcji \(f\) ma dwa punkty wspólne z prostą \(y=2\).

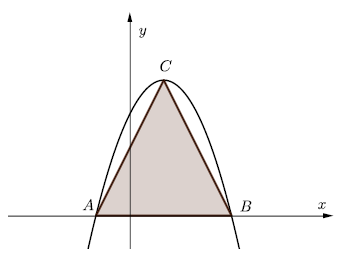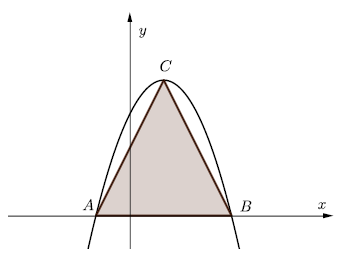Wierzchołki trójkąta \(ABC\) leżą na paraboli, która jest wykresem pewnej funkcji kwadratowej \(f\) (zobacz rysunek). Pole trójkąta jest równe \(8\), punkt \(C=(1,4)\) jest wierzchołkiem paraboli, a punkty \(A\) i \(B\) leżą na osi \(Ox\). Wyznacz wzór funkcji \(f\).

W układzie współrzędnych na płaszczyźnie rysujemy łamane. Kolejne wierzchołki każdej z tych łamanych to punkty: \[A_1=(0,0),\quad A_2=(1,0),\quad A_3=(1,-1),\quad A_4=(-1,-1),\quad A_5=(-1,1),\quad A_6=(2,1)\] i tak dalej. Na rysunku jest przedstawiona łamana składająca się z dziesięciu odcinków, której ostatnim wierzchołkiem jest punkt \(A_{11}=(3,-3)\). Funkcja \(f\) przyporządkowuje każdej liczbie naturalnej \(n\ge 1\) długość łamanej złożonej z \(2n\) odcinków, czyli takiej, której początkowym wierzchołkiem jest punkt \(A_1\), a końcowym \(A_{2n+1}\). Wyznacz wzór funkcji \(f\) oraz oblicz jej wartość dla \(n=33\).