Jednomiany
Definicja
Jednomian - to wyrażenie będące iloczynem liczby i liter (może być też sama liczba lub sama litera). Przykłady jednomianów: \[x,\quad \frac{1}{2}x,\quad x^2,\quad 2xy,\quad 5x^2y^3,\quad -\frac{2}{3}abc\]
Definicja
Liczbę występującą w jednomianie nazywa się współczynnikiem liczbowym jednomianu.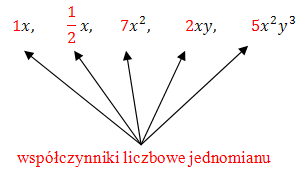
Każdy jednomian musi mieć współczynnik liczbowy. W przypadku, gdy nie jest on zapisany, to znaczy, że jest równy \(1\).
Kolejność zapisywania składników jednomianu nie ma znaczenia (bo mnożenie jest przemienne), ale zazwyczaj zapisujemy współczynnik liczbowy na początku jednomianu, a następnie literki w kolejności alfabetycznej.
Przedstaw jednomian \(2x\cdot 7\) w postaci uporządkowanej i podaj jego współczynnik liczbowy.
Wszystkie liczby wymnażamy i zapisujemy na początku jednomianu: \[2x\cdot 7=2\cdot 7x=14x\] Współczynnik liczbowy tego jednomianu jest równy \(14\).
Przedstaw jednomian \(x^2\cdot 5x\cdot 2\) w postaci uporządkowanej i podaj jego współczynnik liczbowy.
Wszystkie liczby wymnażamy i zapisujemy na początku jednomianu. Dodatkowo wymnażamy \(x\)-y: \[x^2\cdot 5x\cdot 2=5\cdot 2\cdot x^2\cdot x=10x^3\] Współczynnik liczbowy tego jednomianu jest równy \(10\).
Przedstaw jednomian \(x\cdot x^5\cdot x^2\) w postaci uporządkowanej i podaj jego współczynnik liczbowy.
W tym przykładzie występuje tylko jedna literka \(x\) w różnych potęgach. Wymnażamy wszystkie potęgi, zapisując cały jednomian jako jedną potęgę \(x\)-a. \[x\cdot x^5\cdot x^2=x^8\] Współczynnik liczbowy tego jednomianu jest równy \(1\).
Przedstaw jednomian \(2x^2y\cdot 3xyz\) w postaci uporządkowanej i podaj jego współczynnik liczbowy.
Liczbę zapisujemy na początku, a następnie wymnażamy literki: \[2x^2y\cdot 3xyz=6x^3y^2z\] Współczynnik liczbowy tego jednomianu jest równy \(6\).
Wyrażenie algebraiczne - to suma jednomianów. 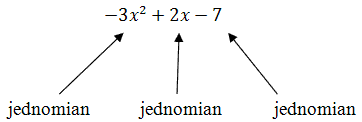

W tym nagraniu wideo omawiam najważniejsze fakty dotyczące jednomianów.