Zadania maturalne CKE 2025 - poziom podstawowy
Poziom podstawowy
Nawigacja do bloków tematycznych:
Liczby rzeczywiste, wyrażenia algebraiczne, równania i nierówności, układy równań
Dokończ zdanie. Zaznacz właściwą odpowiedź spośród podanych.
Wartość wyrażenia \(2024:\left(1-\frac{1}{2025}\right)-\left(1-\frac{2025}{2024}\right): \frac{1}{2024}\) jest równa A.\( 0 \)
B.\( 1 \)
C.\( 2024 \)
D.\( 2026 \)
Pensja pana X jest o \(50\%\) wyższa od średniej krajowej, a pensja pana Y jest o \(40\%\) niższa od średniej krajowej.
Dokończ zdania. Zaznacz odpowiedź spośród A–D oraz odpowiedź spośród E–H.
Pensja pana X jest wyższa od pensji pana Y
A.o \(40\%\) pensji pana Y.
B.o \(90\%\) pensji pana Y.
C.o \(150\%\) pensji pana Y.
D.o \(275\%\) pensji pana Y.
Pensja pana Y jest niższa od pensji pana X
E.o \(60\%\) pensji pana X.
F.o \(73\%\) pensji pana X.
G.o \(90\%\) pensji pana X.
H.o \(150\%\) pensji pana X.
Udowodnij, że dla każdej liczby całkowitej \(n\) liczba \((3 n+5)^2+11 n^2-18\) przy dzieleniu przez \(5\) daje resztę \(2\).
Rozważmy dwie kolejne liczby naturalne \(a\) i \(b\) takie, że \(a\lt b\) oraz obie są niepodzielne przez \(3\).
Udowodnij, że liczba \(a^2+11 a b+b^2\) jest podzielna przez \(9\).
Wykaż, że dla każdej liczby naturalnej \(n \geq 1\) liczba \(n\left(n^2+3 n+2\right)\) jest podzielna przez \(6\).
Dokończ zdanie. Zaznacz właściwą odpowiedź spośród podanych.
Liczba \(\frac{\sqrt[3]{250}+\sqrt[3]{54}}{\sqrt[3]{250}-\sqrt[3]{54}}\) jest równa A.\(\sqrt[3]{\frac{76}{49}}\)
B.\( (-1) \)
C.\( 4 \)
D.\( 4 \sqrt[3]{2} \)
Udowodnij, że liczba \(3^{45}+9^{22}+27^{14}\) jest podzielna przez \(37\).
Dokończ zdanie. Zaznacz właściwą odpowiedź spośród podanych.
Liczba \(|\sqrt{5}-1|-3|2-\sqrt{5}|\) jest równa A.\((-7)\)
B.\(5-4 \sqrt{5}\)
C.\(4 \sqrt{5}-7\)
D.\(5-2 \sqrt{5}\)
Oprocentowanie na długoterminowej lokacie w pewnym banku wynosi \(3\%\) w skali roku (już po uwzględnieniu podatków). Po każdym roku oszczędzania są doliczane odsetki od aktualnego kapitału znajdującego się na lokacie – zgodnie z procentem składanym.
Dokończ zdanie. Zaznacz właściwą odpowiedź spośród podanych.
Po \(10\) latach oszczędzania w tym banku (i bez wypłacania kapitału ani odsetek w tym okresie) kwota na lokacie będzie większa od kwoty wpłaconej na samym początku o (w zaokrągleniu do \(1\%\)) A.\( 30\% \)
B.\( 34\% \)
C.\( 36\% \)
D.\( 43\% \)
Na wykresie przedstawiono zależność \(\log K(t)\), gdzie \(K(t)\) jest liczbą bakterii w próbce po czasie \(t\) wyrażonym w godzinach, jaki upłynął od chwili \(t=0\) rozpoczęcia obserwacji.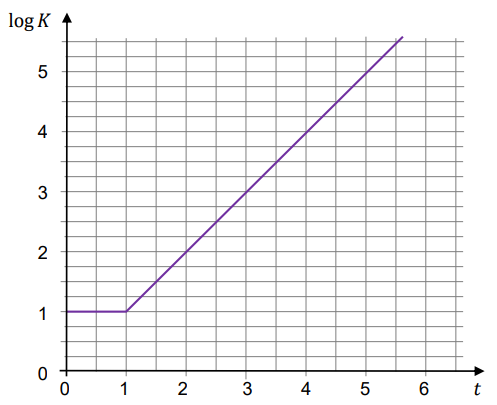 
Dokończ zdanie. Zaznacz właściwą odpowiedź spośród podanych.
Gdy upłynęły dokładnie trzy godziny od chwili \(t=0\), liczba \(K\) bakterii była równa A.\( 3 \)
B.\( 100 \)
C.\( 1000 \)
D.\( 10000 \)
Liczba \(\log_2\left[(\sqrt{2})^2\cdot (\sqrt{2})^4\cdot (\sqrt{2})^8\right]\) jest równa
A.\( \sqrt{2} \)
B.\( 7 \)
C.\( 14 \)
D.\( 2^7 \)
Dane są liczby \(a=\log _2(3 \sqrt{5}+\sqrt{13})\) oraz \(b=\log _2(3 \sqrt{5}-\sqrt{13})\).
Dokończ zdanie. Zaznacz właściwą odpowiedź spośród podanych.
Liczba \(a+b\) jest równa A.\(\log _2 45\)
B.\(\log _2 30\)
C.\(4\)
D.\(5\)
Dane są dwie liczby \(x\) i \(y\), takie, że iloraz \(\frac{x}{y}\) jest równy \(\frac{1+\sqrt{5}}{2}\).
Oblicz wartość wyrażenia \(\frac{x+y}{x}\). Wynik podaj bez niewymierności w mianowniku.
Dane są liczby \(a=\sqrt{5}-2\) oraz \(b=\sqrt{5}+2\).
Oblicz wartość wyrażenia \(\frac{a\cdot b}{\sqrt{a}+\sqrt{b}} : \frac{\sqrt{a}-\sqrt{b}}{a-b}\) dla podanych \(a\) i \(b\).
Dana jest liczba \(x=a-(\sqrt{3}-\sqrt{2})^2\), gdzie \(a\) należy do zbioru \(\mathbb{R} \) liczb rzeczywistych. W rozwiązaniu zadania uwzględnij fakt, że liczby \(\sqrt{3}\) oraz \(\sqrt{2}\cdot \sqrt{3}\) są niewymierne.
Dokończ zdanie. Zaznacz dwie odpowiedzi, tak aby dla każdej z nich dokończenie zdania było prawdziwe.
Liczba \(x\) jest wymierna dla A.\( a=5 \)
B.\( a=-\sqrt{3}+\sqrt{2} \)
C.\( a=(\sqrt{2}-\sqrt{3})^2+0{,}3 \)
D.\( a=6 \)
E.\( a=-2\sqrt{6}+12{,}5 \)
F.\( a=(\sqrt{2}-\sqrt{3})^2-2\sqrt{6} \)
G.\( a=-\sqrt{6} \)
Dane jest wyrażenie \(W(x)=\frac{2 x^2}{x^2-4} \cdot \frac{x-2}{x}\).
Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, albo F – jeśli jest fałszywe.
| Wartość wyrażenia \(W(x)\) jest określona dla każdej liczby rzeczywistej \(x\). | P | F |
| Jeżeli wartość wyrażenia \(W(x)\) jest określona, to \(W(x)=\frac{2 x}{x+2}\). | P | F |
Dana jest nierówność \[ \frac{2 x-1}{2}-\frac{x+2}{3} \geq \frac{1}{6} \]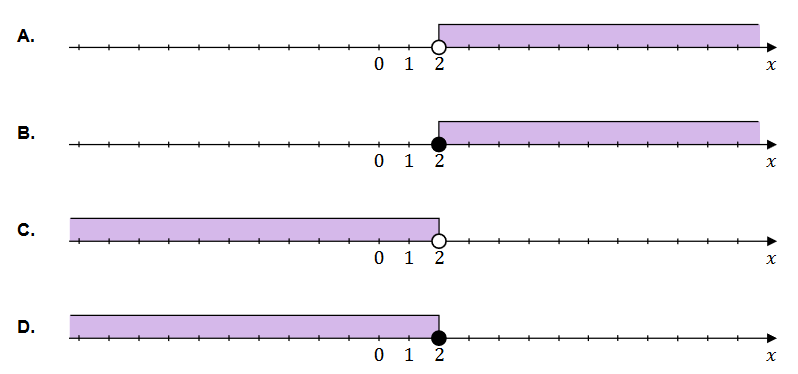 
Na którym rysunku poprawnie zaznaczono na osi liczbowej zbiór wszystkich liczb rzeczywistych spełniających powyższą nierówność? Zaznacz właściwą odpowiedź spośród podanych.
Dane jest równanie \[ \frac{2}{2 x+1}=\frac{x-1}{x+2} \]
Wyznacz dziedzinę tego równania. Rozwiąż to równanie.
Rozwiąż nierówność
\[(3 x-4)(x-1)\lt x\]Rozważmy takie liczby rzeczywiste \(a\) i \(b\), które spełniają warunki:\[a\ne 0,\ b\ne 0\quad \text{oraz}\quad a^3+b^3=(a+b)^3\]
Oblicz wartość liczbową wyrażenia \(\frac{a}{b}\) dla dowolnych liczb rzeczywistych \(a\) i \(b\), spełniających powyższe warunki.
Dokończ zdanie. Zaznacz właściwą odpowiedź spośród podanych.
Układ równań \(\left\{\begin{array}{c}x+2 y=1 \\ -4 x-8 y=-4\end{array}\right.\) A.nie ma rozwiązań.
B.ma dokładnie jedno rozwiązanie.
C.ma dokładnie dwa rozwiązania.
D.ma nieskończenie wiele rozwiązań.
Funkcje, ciągi, optymalizacja
Funkcja \(y=f(x)\) jest określona za pomocą tabeli
| \(x\) | \(-3\) | \(-2\) | \(-1\) | \(0\) | \(1\) | \(2\) | \(3\) |
| \(y\) | \(-3\) | \(2\) | \(0\) | \(1\) | \(0\) | \(2\) | \(1\) |
Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, albo F – jeśli jest fałszywe.
| Funkcja \(f\) ma dokładnie jedno miejsce zerowe. | P | F |
| W kartezjańskim układzie współzędnych \((x, y)\) wykres funkcji \(f\) jest symetryczny względem osi \(O y\). | P | F |
| Największa wartość funkcji \(f\) jest równa \(3\). | P | F |
Dokończ zdanie. Zaznacz właściwą odpowiedź spośród podanych.
W kartezjańskim układzie współrzędnych \((x, y)\) wykresy funkcji liniowych \(f(x)=(2m+7) x+5\) oraz \(g(x)=3x\) nie maja punktów wspólnych dla A.\(m=-2\)
B.\(m=-1\)
C.\(m=1\)
D.\(m=2\)
Dana jest funkcja \(f\) określona wzorem: \[ f(x)=\left\{\begin{array}{cc} 2 x-6 & \text { dla } x \leq 2 \\ x-4 & \text { dla } x\gt 2 \end{array}\right. \]
Dokończ zdanie. Zaznacz właściwą odpowiedź spośród podanych.
Miejscem zerowym funkcji \(f\) jest liczba A.\( (-6) \)
B.\( (-4) \)
C.\( 3 \)
D.\( 4 \)
Dana jest funkcja \(f\) określona wzorem \(f(x)=x^2-b-2 \sqrt{2}\) dla każdej liczby rzeczywistej \(x\). Miejscem zerowym funkcji \(f\) jest \(x=\sqrt{2}+1\).
Dokończ zdanie. Zaznacz właściwą odpowiedź spośród podanych.
Współczynnik \(b\) we wzorze funkcji \(f\) jest równy A.\((-3)\)
B.\(3\)
C.\(3-\sqrt{2}\)
D.\(3-2 \sqrt{2}\)
Funkcja kwadratowa \(f\) jest określona wzorem \(f(x)=3 x^{2}+2 x+m\) dla każdej liczby rzeczywistej \(x\). Współczynnik \(m\) jest liczbą rzeczywistą mniejszą od zera.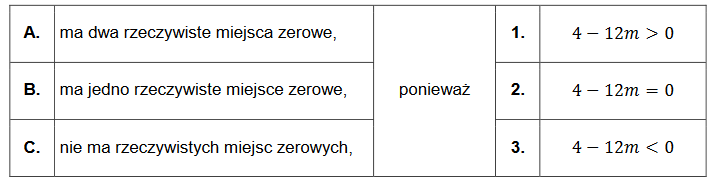 
Dokończ zdanie. Zaznacz odpowiedź A, B albo C oraz jej uzasadnienie 1., 2. albo 3.
Funkcja \(f\) Dana jest funkcja \(y=f(x)\), której wykres przedstawiono w kartezjańskim układzie współrzędnych \((x,y)\) na rysunku.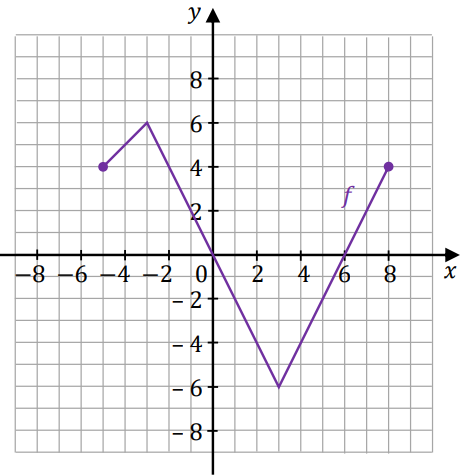 
Ta funkcja jest określona dla każdej liczby rzeczywistej \(x\in [-5,8]\).
Ta funkcja jest określona dla każdej liczby rzeczywistej \(x\in [-5,8]\).Zapisz w miejscu wykropkowanym poniżej zbiór rozwiązań nierówności: \[f(x)\gt 2\]
Zapisz w miejscu wykropkowanym poniżej maksymalny przedział lub maksymalne przedziały, w których funkcja \(f\) jest malejąca.
Uzupełnij zdanie. Wpisz odpowiednie liczby w wykropkowanych miejscach, aby zdanie było prawdziwe.
Największa wartość funkcji \(f\) jest równa liczbie ............... , a najmniejsza wartość funkcji \(f\) jest równa liczbie .......................Funkcja \(f\) jest określona następująco: \[ f(x)= \begin{cases}x+4 & \text { dla } x \in[-8,0] \\ 4 & \text { dla } x \in(0,4] \\ -2 x+12 & \text { dla } x \in(4,6)\end{cases} \] Wykres funkcji \(y=f(x)\) przedstawiono w kartezjańskim układzie współrzędnych \((x, y)\) na rysunku poniżej.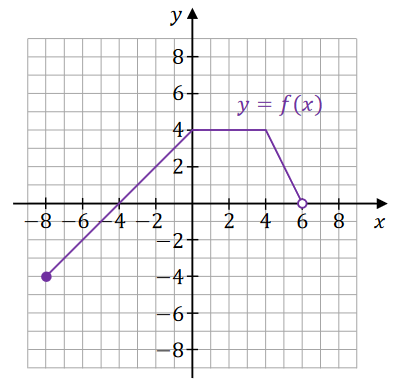 
Uzupełnij zdania. Wpisz odpowiednie przedziały w wykropkowanych miejscach tak, aby zdania były prawdziwe.
- Dziedziną funkcji \(f\) jest przedział \(............\) .
- Zbiorem wartości funkcji \(f\) jest przedział \(............\) .
- Zbiorem wszystkich argumentów, dla których funkcja \(f\) przyjmuje wartości nieujemne, jest przedział \(............\) .
- Zbiorem wszystkich rozwiązań równania \(f(x)=4\) jest przedział \(............\) .
Dana jest funkcja \(y=f(x)\), której wykres przedstawiono w kartezjańskim układzie współrzędnych \((x,y)\) na rysunku.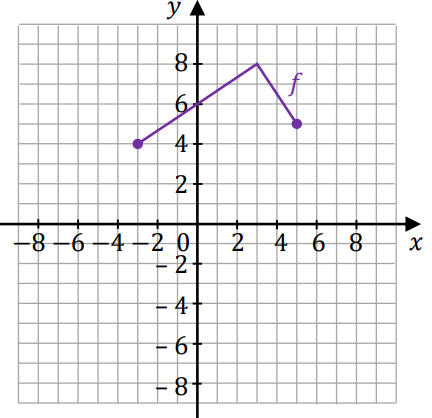 
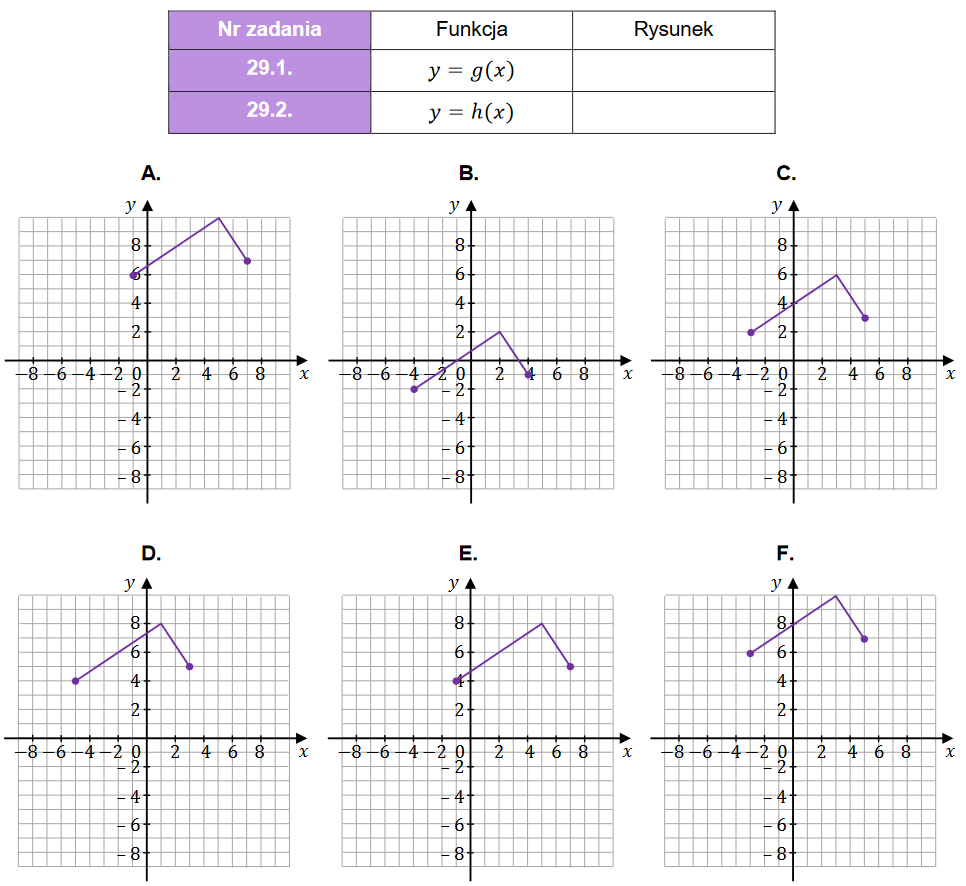
Funkcje \(g\) oraz \(h\) są określone za pomocą funkcji \(f\) następująco: \[y=g(x)=f(x+2)\qquad y=h(x)=f(x)+2\] Na rysunkach A–F przedstawiono wykresy różnych funkcji – w tym wykresy funkcji \(g\) oraz \(h\). 
Funkcje \(g\) oraz \(h\) są określone za pomocą funkcji \(f\) następująco: \[y=g(x)=f(x+2)\qquad y=h(x)=f(x)+2\] Na rysunkach A–F przedstawiono wykresy różnych funkcji – w tym wykresy funkcji \(g\) oraz \(h\). Każdej z funkcji \(y=g(x)\) oraz \(y=h(x)\) przyporządkuj jej wykres. Wpisz obok symboli funkcji w tabeli poniżej właściwe odpowiedzi wybrane spośród A–F.
Na podstawie zasad dynamiki można udowodnić, że torem rzutu – przy pominięciu oporów powietrza - jest fragment paraboli. Koszykarz wykonał rzut do kosza z odległości \(x_k=7{,}01\) m, licząc od środka piłki do środka obręczy kosza w linii poziomej. Do opisu toru ruchu przyjmiemy układ współrzędnych, w którym środek piłki w chwili początkowej znajdował się w punkcie \(x_0=0\), \(y_0 = 2{,}50\) m. Środek piłki podczas rzutu poruszał się po paraboli danej równaniem: \[y = −0{,}174x^2 + 1{,}3x + 2{,}5\] Rzut okazał się udany, a środek piłki przeszedł dokładnie przez środek kołowej obręczy kosza. Na rysunku poniżej przedstawiono tę sytuację oraz tor ruchu piłki w układzie współrzędnych.
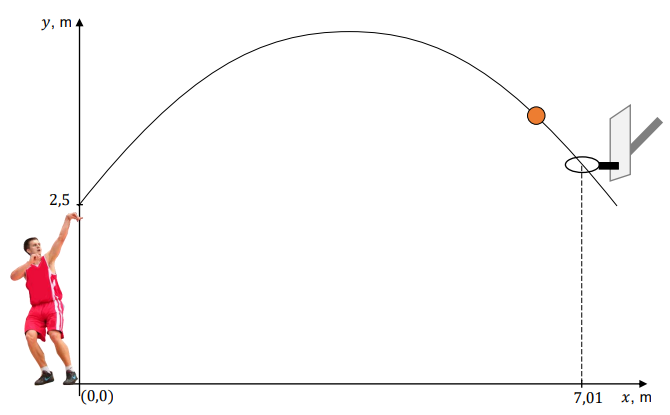
Dokończ zdanie. Zaznacz właściwą odpowiedź spośród podanych. Obręcz kosza znajduje się na wysokości (podanej w zaokrągleniu z dokładnością do 0,01 m)
A.\( 3{,}04 \) m
B.\( 3{,}06 \) m
C.\( 3{,}80 \) m
D.\( 4{,}93 \) m
Oblicz wysokość maksymalną, na jaką wzniesie się środek piłki podczas opisanego rzutu. Zapisz wynik w zaokrągleniu do drugiego miejsca po przecinku.
W opisanym rzucie piłka przeleciała swobodnie przez obręcz kosza i upadła na parkiet. Przyjmij, że obręcz kosza nie miała siatki, a na drodze rzutu nie było żadnej przeszkody. Promień piłki jest równy \(0{,}12\) m.
Oblicz współrzędną \(x\) punktu środka piłki w momencie, w którym piłka dotknęła parkietu. Zapisz wynik w zaokrągleniu do drugiego miejsca po przecinku.
Czas \(T\) połowicznego rozpadu izotopu promieniotwórczego to czas, po którym liczba jąder danego izotopu (a zatem i masa tego izotopu) zmniejsza się o połowę – tzn. połowa jąder danego izotopu przemienia się w inne jądra. Liczba jąder \(N(t)\) izotopu promieniotwórczego pozostających w próbce po czasie \(t\), licząc od chwili \(t_0 = 0\), wyraża się zależnością wykładniczą: \[N(t)=N_0\left(\frac{1}{2}\right)^{\frac{t}{T}}\] gdzie \(N_0\) jest liczbą jąder izotopu promieniotwórczego w chwili początkowej \(t_0 = 0\).
Na poniższych rysunkach 1.-4. przedstawiono wykresy różnych zależności.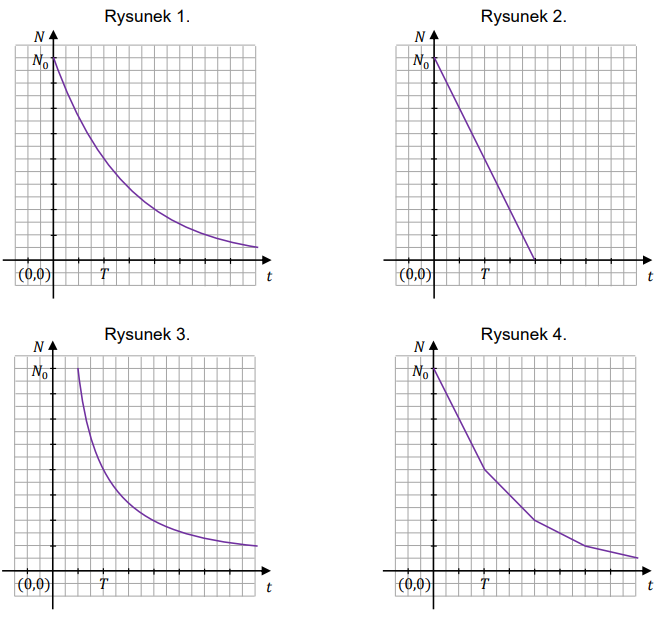 
Dokończ zdanie. Zaznacz właściwą odpowiedź spośród podanych.
Wykres zależności wykładniczej \(N(t)\) - opisanej we wstępie do zadania - przedstawiono na A.rysunku 1.
B.rysunku 2.
C.rysunku 3.
D.rysunku 4.
Czas połowicznego rozpadu węgla \(^{14}\text{C}\) to około \(5700\) lat. Naukowcy oszacowali za pomocą datowania radiowęglowego, że masa izotopu węgla \(^{14}\text{C}\) w pewnym organicznym znalezisku archeologicznym stanowi \(\frac{1}{16}\) masy tego izotopu, jaka utrzymywała się podczas życia organizmu. 
Oblicz, ile lat ma opisane znalezisko archeologiczne. Wynik podaj z dokładnością do stu lat.
Dany jest ciąg \((a_n)\) określony wzorem rekurencyjnym: \[\begin{cases} a_1 = -2 \\ a_{n+1} = n\cdot a_n + 4 \end{cases} \] dla każdej liczby naturalnej \(n \ge 1\).
Oblicz sumę czterech początkowych wyrazów ciągu \((a_n)\).
Dany jest ciąg \((a_n)\) określony wzorem ogólnym: \(a_n = 4n - 9\) dla każdej liczby naturalnej \(n \ge 1\).
Wykaż, że ciąg \((a_n)\) jest arytmetyczny.
Dokończ zdanie. Zaznacz odpowiedź A, B albo C oraz jej uzasadnienie 1., 2. albo 3.
Ciąg \(\left(a_{n}\right)\) określony wzorem \(a_{n}=n^{2}-n\) dla każdej liczby naturalnej \(n \geq 1\) jest 
Funkcja \(f\) jest określona wzorem \(f(x) = \frac{1}{x}\) dla każdej liczby rzeczywistej \(x \ne 0\).
Oblicz wartość \(m\), dla której liczby \(f(m)\), \(f(1)\), \(f(2)\) są - odpowiednio - pierwszym, drugim i trzecim wyrazem ciągu geometrycznego.
Powierzchnia magazynowa będzie się składała z dwóch identycznych prostokątnych działek połączonych wspólnym bokiem. Całość ma być ogrodzona płotem, przy czym obie działki będzie rozdzielał wspólny płot. W ogrodzeniu będą zamontowane dwie bramy wjazdowe, każda o szerokości \(10\) m (zobacz rysunek poniżej). Łączna długość płotu ogradzającego oraz rozdzielającego obie działki wyniesie \(580\) metrów, przy czym szerokości obu bram wjazdowych nie wliczają się w długość płotu.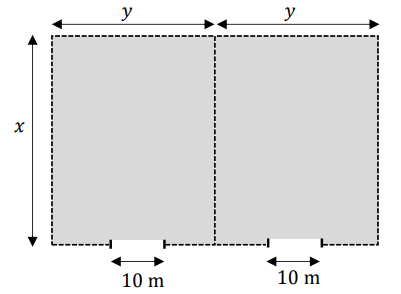 
Oblicz wymiary \(x\) i \(y\) każdej z dwóch prostokątnych działek, tak aby całkowite pole powierzchni magazynowej było największe.
Trygonometria, planimetria, geometria analityczna, stereometria
Dany jest kąt o mierze \(\alpha\) taki, że \(\sin\alpha = \frac{4}{5}\) oraz 9\(0^\circ \lt \alpha \lt 180^\circ\).
Oceń prawdziwość poniższych zdań. Zaznacz P, jeśli zdanie jest prawdziwe, albo F - jeśli jest fałszywe.
Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, albo F – jeśli jest fałszywe. | Dla kąta \(\alpha\) spełnione jest równanie: \(\cos \alpha =-\frac{3}{5}\). | P | F |
| Dla kąta \(\alpha\) spełnione jest równanie: \(|\operatorname{tg} \alpha |=\frac{3}{4}\) | P | F |
W trójkącie \(ABC\) dane są długości dwóch boków \(|AB| = 12\), \(|BC| = 8\) oraz miara kąta \(|\sphericalangle ABC| = 60^\circ\).
Oblicz długość środkowej tego trójkąta, poprowadzonej z wierzchołka \(A\).
Wierzchołki \(A\) i \(C\) trójkąta \(ABC\) leżą na okręgu o promieniu \(r\). Środek \(S\) tego okręgu leży na boku \(AB\) tego trójkąta (zobacz rysunek poniżej). Długości boków \(AB\) i \(AC\) są równe odpowiednio \(|AB| = 3r\) oraz \(|AC| = \sqrt{3}r\).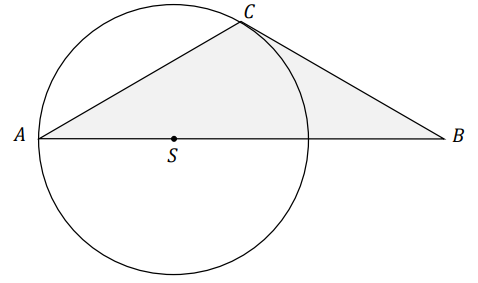 
Oblicz miary wszystkich kątów wewnętrznych trójkąta \(ABC\).
Punkt \(S\) jest środkiem ciężkości trójkąta \(ABC\). Długość odcinka \(SA\) jest równa \(10\).
Dokończ zdanie. Zaznacz właściwą odpowiedź spośród podanych.
Długość środkowej poprowadzonej z wierzchołka \(A\) do boku \(B C\) jest równa A.\( 10 \)
B.\( 15 \)
C.\( 20 \)
D.\( 30 \)
Dane są okrąg o środku \(S\) oraz prosta \(k\) styczna do okręgu w punkcie \(A\). Odcinek \(AB\) jest cięciwą tego okręgu. Miara kąta ostrego pomiędzy prostą \(k\) a cięciwą \(AB\) jest równa \(50^{\circ}\). Punkt \(C\) leży na okręgu. Kąt wpisany \(BCA\) jest ostry. Sytuację przedstawia rysunek poniżej.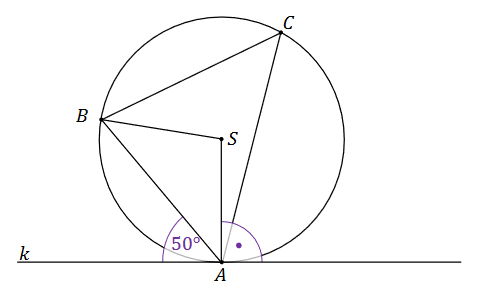 
Dokończ zdanie. Zaznacz właściwą odpowiedź spośród podanych.
Miara kąta wpisanego \(BCA\) jest równa A.\(100^{\circ}\)
B.\(80^{\circ}\)
C.\(50^{\circ}\)
D.\(40^{\circ}\)
Dany jest trójkąt prostokątny \(A B C\) o bokach \(|A C|=12,|B C|=5,|A B|=13\). Dwusieczne kątów tego trójkąta przecinają się w punkcie \(P\) (zobacz rysunek).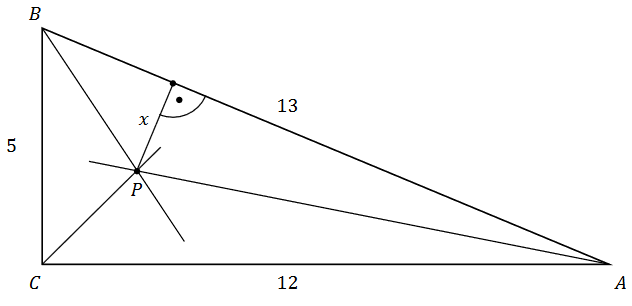 
Dokończ zdanie. Zaznacz właściwą odpowiedź spośród podanych.
Odległość \(x\) punktu \(P\) od przeciwprostokątnej \(AB\) jest równa A.\( 1 \)
B.\( 2 \)
C.\( \frac{5}{2} \)
D.\( \frac{20}{13} \)
Dany jest trójkąt \(ABC\). Na boku \(AB\) tego trójkąta wybrano punkt \(D\), taki, że \(|AD| = \frac{1}{4}|AB|\), a na boku \(BC\) wybrano taki punkt \(E\), że \(|BE| = \frac{1}{5}|BC|\) (zobacz rysunek poniżej). Pole trójkąta \(ABC\) jest równe \(20\).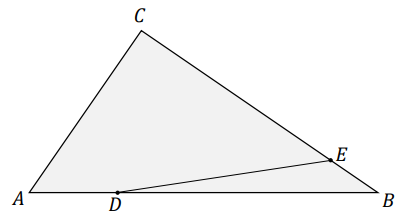 
Oblicz pole trójkąta \(DBE\).
Na podstawie twierdzenia Pitagorasa można udowodnić bardziej ogólną własność niż ta, o której mówi samo to twierdzenie.
Rozważmy trójkąt prostokątny \(ABC\) o kącie prostym przy wierzchołku \(A\). Niech każdy z boków tego trójkąta: \(CA\), \(AB\), \(BC\) będzie podstawą trójkątów podobnych, odpowiednio: \(CAW_1\), \(ABW_2\), \(CBW_3\). Trójkąty te mają odpowiadające sobie kąty o równych miarach, odpowiednio przy wierzchołkach: \(W_1, W_2, W_3\).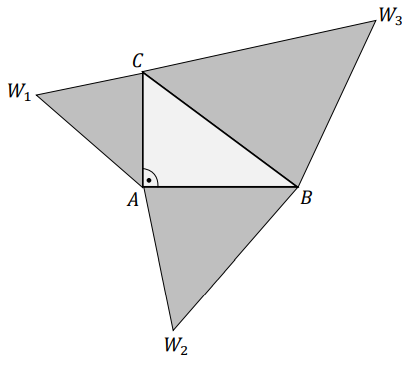 
Pola trójkątów: \(CAW_1\), \(ABW_2\), \(CBW_3\) oznaczymy odpowiednio jako \(P_1\), \(P_2\), \(P_3\). Udowodnij, że: \[P_3=P_1+P_2\]Dany jest prostokąt \(ABCD\), w którym \(|AD| = 2\). Kąt \(BDA\) ma miarę \(\alpha\), taką, że \(\operatorname{tg} \alpha = 2\). Przekątna \(BD\) i prosta przechodząca przez wierzchołek \(C\) prostopadła do \(BD\) przecinają się w punkcie \(E\) (zobacz rysunek).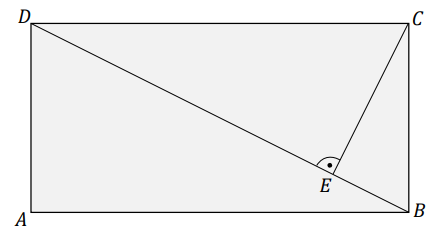 
Oblicz długość odcinka \(CE\).
Trzy różne punkty \(A\), \(B\) i \(D\) leżą na okręgu o środku w punkcie \(S\). Odcinek \(BD\) jest średnicą tego okręgu. Styczne \(k\) i \(l\) do tego okręgu, odpowiednio w punktach \(A\) i \(B\), przecinają się w punkcie \(C\) (zobacz rysunek poniżej).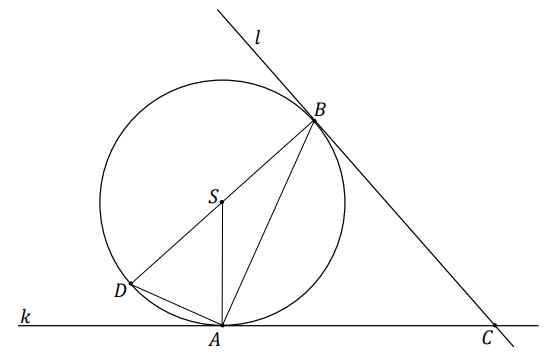 
Wykaż, że trójkąty \(ACB\) i \(ASD\) są podobne.
Dany jest trójkąt \(ABC\) o bokach długości: \(|AB| = 4\), \(|BC| = 5\), \(|AC| = 6\).
Oblicz sinus najmniejszego kąta wewnętrznego trójkąta \(ABC\).
Proste \(k\) i \(l\) przecinają się w punkcie \(A\). Proste \(m\), \(n\) i \(s\) są do siebie równoległe i przecinają obie proste \(k\) i \(l\) w punktach \(B, C, D, E, F, G\) (zobacz rysunek poniżej), w taki sposób, że: \[|BC| = 30,\quad |CD| = 20,\quad |GF| = 21\].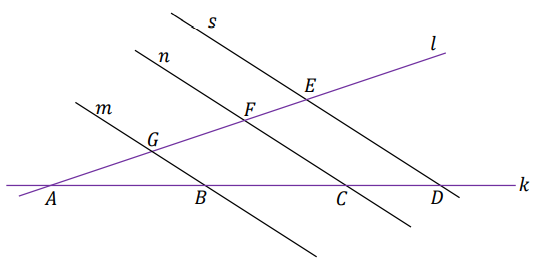 
Oblicz długość odcinka \(FE\).
Na płaszczyźnie, w kartezjańskim układzie współrzędnych \((x, y)\), dany jest okrąg \(\mathcal{O}\) określony równaniem: \[ (x-2)^2+(y+3)^2=16 \] 2. Promień \(r\) okręgu \(\mathcal{O}\) jest równy
Dokończ zdania. Zaznacz odpowiedź spośród A-D oraz odpowiedź spośród E-G.
1. Ṡrodek \(S\) okręgu \(\mathcal{O}\) ma współrzędne A.\(S=(2,-3)\)
B.\(S=(-2,-3)\)
C.\(S=(-2,3)\)
D.\(S=(-2,3)\)
E.\(r=16\)
F.\(r=4\)
G.\(r=5\)
Na płaszczyźnie, w kartezjańskim układzie współrzędnych \((x, y)\), dane są punkty \(A = (1,2)\) oraz \(B = (3,7)\). Punkty \(A_O\) oraz \(B_O\) są odpowiednio obrazami punktów \(A\) i \(B\) w symetrii środkowej o środku w punkcie \(O = (0,0)\).
Dokończ zdanie. Zaznacz właściwą odpowiedź spośród podanych.
Współczynnik kierunkowy prostej przechodzącej przez punkty \(A_O\) i \(B_O\) jest równy A.\( \frac{5}{2} \)
B.\( -\frac{5}{2} \)
C.\( \frac{2}{5} \)
D.\( -\frac{2}{5} \)
Na płaszczyźnie, w kartezjańskim układzie współrzędnych \((x, y)\), dany jest trapez \(A B C D\), w którym boki \(AB\) i \(CD\) są równoległe oraz \(C=(3,15)\). Wierzchołki \(A\) i \(B\) tego trapezu leżą na prostej o równaniu \(3x-y+10=0\).
Dokończ zdanie. Zaznacz właściwą odpowiedź spośród podanych.
Bok \(CD\) tego trapezu zawiera się w prostej o równaniu A.\(y=3 x+15\)
B.\(y=3 x+6\)
C.\(y=\frac{5}{3} x+10\)
D.\(y=-\frac{1}{3} x+16\)
Na płaszczyźnie, w kartezjańskim układzie współrzędnych \((x, y)\), punkty \(A=(-1,-5)\), \(B=(2,-7), C=(6,9)\) i \(D=(-2,9)\) są wierzchołkami czworokąta \(ABCD\).
Oblicz współrzędne punktu przecięcia przekątnych czworokąta \(ABCD\).
W kartezjańskim układzie współrzędnych \((x, y)\) przekątne równoległoboku \(A B C D\) przecinają się w punkcie \(S=\left(\frac{11}{2}, \frac{17}{2}\right)\). Bok \(A B\) tego równoległoboku zawiera się w prostej o równaniu \(y=x-2\), a bok \(A D\) zawiera się w prostej o równaniu \(y=3 x-6\).
Oblicz współrzędne wierzchołka \(B\).
W kartezjańskim układzie współrzędnych \((x, y)\) punkty \(A=(2,8)\) oraz \(B=(10,2)\) są wierzchołkami trójkąta równoramiennego \(ABP\), w którym \(|AP|=|BP|\). Wierzchołek \(P\) leży na osi \(O x\) układu współrzędnych.
Oblicz współrzędne punktu \(P\) oraz długość odcinka \(AP\).
Dany jest prostopadłościan \(ABCDEFGH\), w którym prostokąty \(ABCD\) i \(EFGH\) są jego postawami. Odcinek \(BH\) jest przekątną tego prostopadłościanu.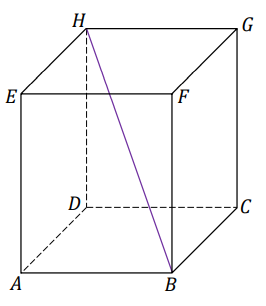 
Na którym rysunku prawidłowo narysowano, oznaczono i podpisano kąt \(\alpha \) pomiędzy przekątną \(BH\) prostopadłościanu a jego ścianą boczną \(ADHE\)? Zaznacz właściwą odpowiedź spośród podanych.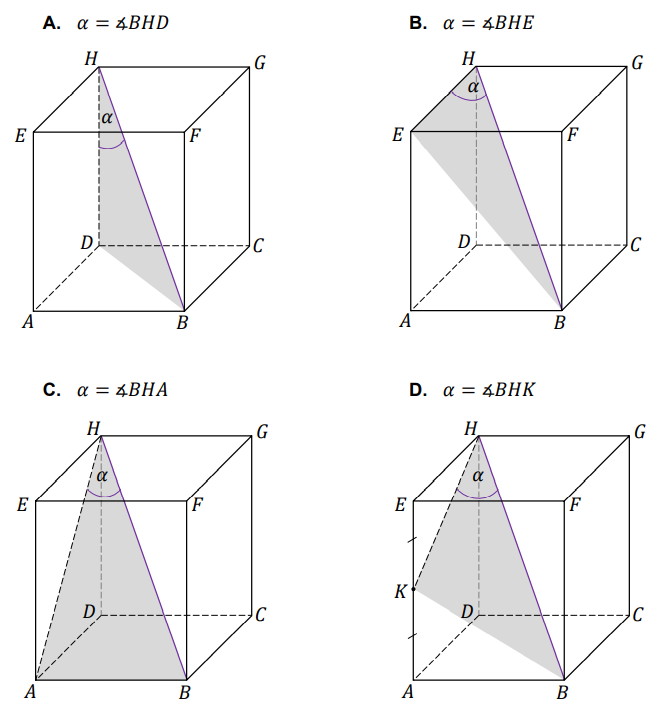 
W prostopadłościanie \(ABCDEFGH\) dane są: \[\operatorname{tg} \beta =\frac{9}{7}\quad |BG|=2\cdot \sqrt{130}\quad |BH|=2\cdot \sqrt{194}\] gdzie odcinek \(BH\) jest przekątną prostopadłościanu, odcinek \(BG\) jest przekątną ściany bocznej \(BCGF\), \(\beta \) jest miarą kąta \(\sphericalangle GBC\). Sytuację ilustruje rysunek poniżej.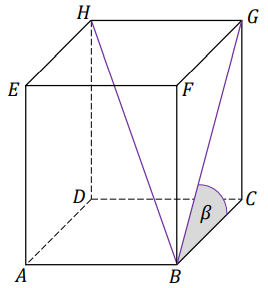 
Oblicz pole powierzchni całkowitej prostopadłościanu \(ABCDEFGH\).
Dane są dwa prostopadłościany podobne: \(B_1\) oraz \(B_2\). Objętość prostopadłościanu \(B_1\) jest równa \(V\), a objętość prostopadłościanu \(B_2\) jest równa \(27V\). Pole powierzchni całkowitej prostopadłościanu \(B_1\) jest równe \(P\).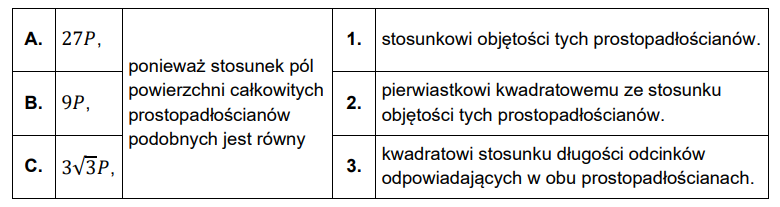 
Dokończ zdanie. Zaznacz odpowiedź A, B albo C oraz jej uzasadnienie 1., 2. albo 3.
Pole powierzchni całkowitej prostopadłościanu \(B_2\) jest równe Hania zaprojektowała i wykonała czapeczkę na bal urodzinowy młodszego brata. Czapeczka miała kształt powierzchni bocznej stożka o średnicy podstawy \(d = 20\) cm, wysokości \(H = 25\) cm i tworzącej \(l\). 
Żeby wykonać czapeczkę, Hania najpierw narysowała na kartonie figurę płaską \(ABS\) o kształcie wycinka koła o promieniu \(l\) i środku \(S\) (zobacz rysunek 1.). Następnie wycięła tę figurę z kartonu, odpowiednio ją wymodelowała i skleiła odcinek \(SB\) z odcinkiem \(SA\) (zobacz rysunek 2.).
Do obliczeń przyjmij, że rzeczywiste figury są idealne. Dokończ zdanie. Zaznacz właściwą odpowiedź spośród podanych.
Kąt rozwarcia stożka, którego powierzchnią boczną jest czapeczka, ma miarę (w zaokrągleniu do \(1^\circ\)) A.\( 44^\circ \)
B.\( 136^\circ \)
C.\( 22^\circ \)
D.\( 68^\circ \)
Oblicz miarę kąta \(\sphericalangle BSA\) wycinka koła, z którego powstała powierzchnia boczna stożka opisanego we wstępie do zadania. Miarę kąta \(\sphericalangle BSA\) podaj w zaokrągleniu do jednego stopnia.
Dany jest ostrosłup prawidłowy czworokątny. Ściana boczna tego ostrosłupa jest nachylona do płaszczyzny podstawy pod kątem \(30^{\circ}\), a krawędź podstawy ma długość równą \(6 \sqrt{3}\).
Oblicz objętość i pole powierzchni całkowitej tego ostrosłupa.
Pole powierzchni bocznej walca jest równe \(16 \pi\), a promień jego podstawy ma długość \(2\).
Dokończ zdanie. Zaznacz właściwą odpowiedź spośród podanych.
Objętość tego walca jest równa A.\( 16 \)
B.\( 32 \)
C.\( 16 \pi \)
D.\( 32 \pi \)
Kombinatoryka, rachunek prawdopodobieństwa, statystyka
Pojedynczy znak w piśmie Braille’a dla niewidomych jest kombinacją od 1 do 6 wypukłych punktów, które mogą zajmować miejsca ułożone w dwóch kolumnach po trzy miejsca w każdej kolumnie. Poniżej podano przykład napisu w piśmie Braille’a. Czarne kropki w znaku oznaczają wypukłości, a białe kropki oznaczają brak wypukłości. Pojedynczy znak w piśmie Braille’a musi zawierać co najmniej jeden punkt wypukły.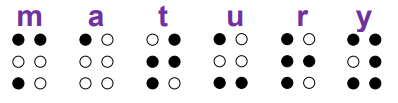 
Oblicz, ile różnych pojedynczych znaków można zapisać w piśmie Braille’a.
Oblicz, ile różnych pojedynczych znaków można zapisać w piśmie Braille’a.Andrzej ma w szafie \(4\) koszule: czerwoną, żółtą, zieloną i niebieską; \(3\) pary spodni: niebieskie, czarne i szare; oraz \(5\) par butów: czarne, szare, zielone, czerwone i niebieskie. 
Andrzej wybiera z szafy zestaw ubrania: jedną koszulę, jedną parę spodni i jedną parę butów. Zestawy ubrania wybierane przez Andrzeja określimy jako różne, gdy będą różniły się kolorem chociaż jednego rodzaju elementu ubioru w zestawie.
Dokończ zdanie. Zaznacz właściwą odpowiedź spośród podanych.
Liczba wszystkich możliwych, różnych zestawów ubrania, jakie może wybrać Andrzej, jest równa A.\( 12 \)
B.\( 72 \)
C.\( 60 \)
D.\( 720 \)
Oblicz, na ile sposobów można wybrać taki zestaw, w którym dokładnie jeden element ubioru będzie niebieski.
Spośród wszystkich czterocyfrowych całkowitych liczb dodatnich losujemy jedną liczbę.
Oblicz prawdopodobieństwo zdarzenia polegającego na tym, że wylosowana liczba będzie parzysta, a w jej zapisie dziesiętnym wystąpią dokładnie jedna cyfra \(2\) i dokładnie jedna cyfra \(3\).
Na wykresie słupkowym poniżej podano rozkład miesięcznych zarobków wszystkich pracowników w pewnej firmie \(F\). Na osi poziomej podano - wyrażone w tysiącach złotych - miesięczne wynagrodzenie netto pracowników firmy \(F\), a na osi pionowej przedstawiono liczbę osób, która osiąga podane zarobki.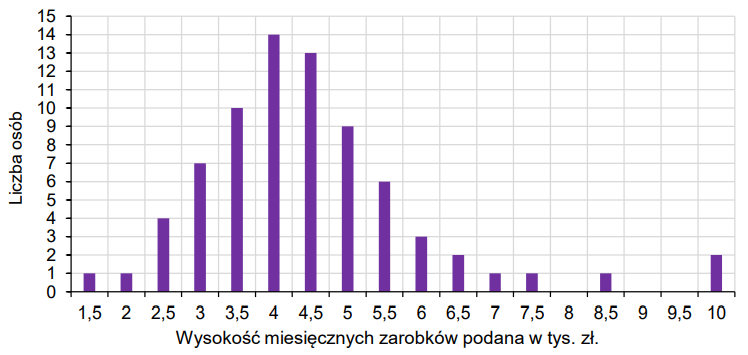 
Dokończ zdanie. Zaznacz odpowiedź A, B albo C oraz jej uzasadnienie 1., 2. albo 3.
Dominantą miesięcznych zarobków w firmie \(F\) jest 
Uzupełnij zdanie. Wpisz odpowiednią liczbę w wykropkowanym miejscu, aby zdanie było prawdziwe.
Medianą miesięcznych zarobków w firmie \(F\) jest ................. tys. zł.Oblicz, jaki \(\%\) liczby wszystkich pracowników firmy \(F\) stanowią osoby zarabiające \(5{,}5\) tys. zł lub mniej.
Oblicz średnią miesięcznego wynagrodzenia netto wszystkich pracowników firmy \(F\). Wynik podaj bez zaokrąglania.
Ze zbioru sześciu liczb \(\{1,2,3,4,5,6\}\) losujemy ze zwracaniem kolejno dwa razy po jednej liczbie.
Oblicz prawdopodobieństwo zdarzenia \(A\) polegającego na tym, że pierwsza wylosowana liczba będzie większa od drugiej wylosowanej liczby.
Tematy nadrzędne i sąsiednie