Rysowanie wykresu funkcji
Poziom podstawowy
Definicja
Wykresem funkcji \(f:X\rightarrow Y \) nazywamy zbiór wszystkich punktów \((x,y)\), takich, że \(x\in X\) oraz \(y=f(x)\).Funkcja \(f\) przyporządkowuje każdemu argumentowi liczbę o \(5\) większą. Dziedziną funkcji \(f\) jest zbiór \(\{-1,0,1,2,3\}\). Wyznacz zbiór wartości tej funkcji oraz narysuje jej wykres.
Zaczynamy od wyznaczenia wartości: \[ \begin{split} &f(-1)=-1+5=4\\[6pt] &f(0)=0+5=5\\[6pt] &f(1)=1+5=6\\[6pt] &f(2)=2+5=7\\[6pt] &f(3)=3+5=8\\[6pt] \end{split} \] Zatem zbiór wartości to: \(\{4,5,6,7,8\}\).
Czyli wykres będą tworzyły punkty o współrzędnych: \[ \begin{split} &(-1,4)\\[6pt] &(0,5)\\[6pt] &(1,6)\\[6pt] &(2,7)\\[6pt] &(3,8)\\[6pt] \end{split} \] Rysujemy wykres: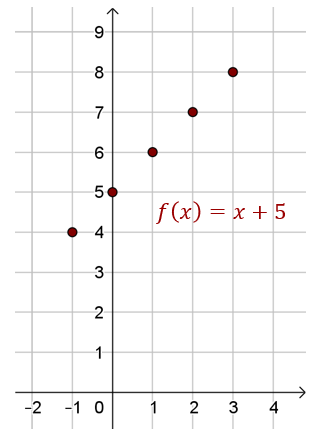 W tym przykładzie dziedziną funkcji był skończony zbiór argumentów (dokładnie \(5\) argumentów), dlatego wykresem funkcji był skończony zbiór punktów (dokładnie \(5\) punktów).
W tym przykładzie dziedziną funkcji był skończony zbiór argumentów (dokładnie \(5\) argumentów), dlatego wykresem funkcji był skończony zbiór punktów (dokładnie \(5\) punktów).
Czyli wykres będą tworzyły punkty o współrzędnych: \[ \begin{split} &(-1,4)\\[6pt] &(0,5)\\[6pt] &(1,6)\\[6pt] &(2,7)\\[6pt] &(3,8)\\[6pt] \end{split} \] Rysujemy wykres:
 W tym przykładzie dziedziną funkcji był skończony zbiór argumentów (dokładnie \(5\) argumentów), dlatego wykresem funkcji był skończony zbiór punktów (dokładnie \(5\) punktów).
W tym przykładzie dziedziną funkcji był skończony zbiór argumentów (dokładnie \(5\) argumentów), dlatego wykresem funkcji był skończony zbiór punktów (dokładnie \(5\) punktów). Rozważmy teraz funkcję \(g\), która także przyporządkowuje każdemu argumentowi liczbę o \(5\) większą, ale której dziedziną jest zbiór wszystkich liczb rzeczywistych \(\mathbb{R} \).
Możemy zapisać wzór funkcji \(g\): \[g(x)=x+5\] oraz obliczyć kilka przykładowych wartości: \[ \begin{split} &g(-1)=-1+5=4\\[6pt] &g(0)=0+5=5\\[6pt] &g(1)=1+5=6\\[6pt] &g(2)=2+5=7\\[6pt] &g(3)=3+5=8\\[6pt] \end{split} \] Wykres funkcji \(g\), będzie przechodził przez wszystkie punkty wykresu funkcji \(f\) z poprzedniego przykładu i będzie linią prostą: 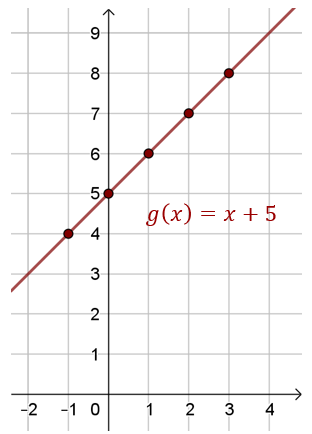 Jest to funkcja liniowa i zbiorem jej wartości jest zbiór wszystkich liczb rzeczywistych \(\mathbb{R} \).
Jest to funkcja liniowa i zbiorem jej wartości jest zbiór wszystkich liczb rzeczywistych \(\mathbb{R} \). Jak widać na powyższym przykładzie, wykres funkcji można narysować wyznaczając dostatecznie dużo punktów należących do tego wykresu. Dla funkcji liniowej wystarczy wyznaczyć tylko dwa punkty, przez które przechodzi prosta, aby ją narysować.
Narysuj wykres funkcji \(y = x + 2\).
Zaczynamy od wyznaczenia kilku punktów należących do tego wykresu.
Tym razem zapiszemy obliczenia w tabelce:
Tym razem zapiszemy obliczenia w tabelce:
| \(x\) | \(-2\) | \(-1\) | \(0\) | \(1\) | \(2\) | \(3\) | \(4\) |
| \(y=x+2\) | \(0\) | \(1\) | \(2\) | \(3\) | \(4\) | \(5\) | \(6\) |
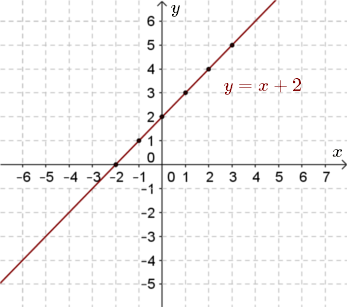
Zatem do wykresu funkcji należą punkty: \((-2, 0), (-1, 1), (0, 2), (1, 3), (2, 4), (3, 5)\).
Zaznaczamy te punkty w układzie współrzędnych, a następnie łączymy linią: 
Do narysowania wykresu funkcji liniowej wystarczyło wyznaczenie dwóch punktów. My wyznaczyliśmy ich więcej dla treningu.
W tym przykładzie mieliśmy dany wzór funkcji w postaci: \[y=x+2\] Ale równie dobrze można było go zapisać tak: \[f(x)=x+2\] Oba zapisy są równoważne.
Narysuj wykres funkcji \(y = x - 5\).
Zaczynamy od wyznaczenia punktów należących do tego wykresu. Tworzymy tabelkę:
Zatem do wykresu tej funkcji należą takie punkty jak: \((-2, -7), (-1, -6), (0, -5), (1, -4), (2, -3), (3, -2)\).
Teraz zaznaczamy te punkty w układzie współrzędnych i rysujemy wykres: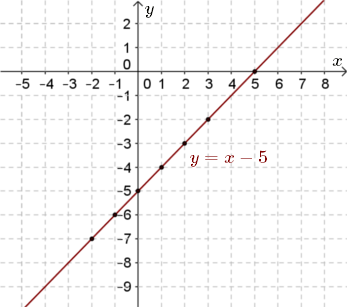
| \(x\) | \(-2\) | \(-1\) | \(0\) | \(1\) | \(2\) | \(3\) |
| \(y=x-5\) | \(-7\) | \(-6\) | \(-5\) | \(-4\) | \(-3\) | \(-2\) |
Teraz zaznaczamy te punkty w układzie współrzędnych i rysujemy wykres:

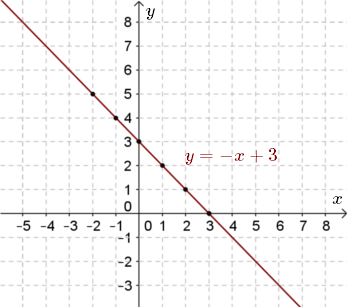
Narysuj wykres funkcji \(y = -x + 3\).
Obliczamy punkty należące do wykresu i zapisujemy wyniki w tabelce:
| \(x\) | \(-2\) | \(-1\) | \(0\) | \(1\) | \(2\) | \(3\) |
| \(y=-x+3\) | \(5\) | \(4\) | \(3\) | \(2\) | \(1\) | \(0\) |
Zatem do wykresu funkcji należą punkty : \((-2, 5), (-1, 4), (0, 3), (1, 2), (2, 1), (3, 0)\).
Teraz zaznaczamy te punkty w układzie współrzędnych i rysujemy wykres: 
Definicje (mało istotne)
Czasami możemy spotkać takie pojęcia:- oś odciętych - to inna nazwa osi \(x\)-ów
- oś rzędnych - to inna nazwa osi \(y\)-ów
W tym nagraniu wideo pokazuję co to jest oś odciętych i oś rzędnych.
Tematy nadrzędne i sąsiednie