Definicja funkcji
Poziom podstawowy
Funkcja przyporządkowuje każdemu elementowi jednego zbioru, dokładnie jednego elementu drugiego zbioru.
Definicje
Funkcja ze zbioru \(X\) w zbiór \(Y\), to przyporządkowanie, w którym każdemu elementowi \(x\in X\) odpowiada dokładnie jeden element \(y\in Y\). \[f: X \rightarrow Y \] Zbiór \(X\) nazywamy dziedziną funkcji.
Elementy \(x\in X\) nazywamy argumentami.
Elementy \(x\in X\) nazywamy argumentami.
Zbiór \(Y\) nazywamy przeciwdziedziną funkcji.
Elementy \(y\in Y\), które są przyporządkowane przynajmniej jednemu argumentowi \(x\in X\), nazywamy wartościami funkcji.
Zbiór wartości - to zbiór wszystkich wartości funkcji.
Elementy \(y\in Y\), które są przyporządkowane przynajmniej jednemu argumentowi \(x\in X\), nazywamy wartościami funkcji.
Zbiór wartości - to zbiór wszystkich wartości funkcji.
Funkcje najczęściej oznaczamy małymi literami: \(f, g, h\).
Wartość, którą funkcja \(f\) przyjmuje dla argumentu \(x\) oznaczamy \(f(x)\).
Wartość, którą funkcja \(f\) przyjmuje dla argumentu \(x\) oznaczamy \(f(x)\).
Przydatna informacja
Przeciwdziedzina funkcji nie zawsze musi być określona i samo pojęcie przeciwdziedziny jest rzadko stosowane.Dużo ważniejsza jest dziedzina funkcji, która zawsze musi być określona i z niej bezpośrednio wynika zbiór wartości funkcji.
Weźmy dwa zbiory: 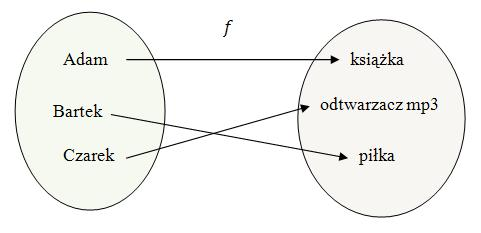 Takie przyporządkowanie nazywamy funkcją.
Takie przyporządkowanie nazywamy funkcją.
Powiemy, że:
- Zbiór chłopców, do którego należą: Adam, Bartek i Czarek.
- Zbiór przedmiotów: piłkę, książkę i odtwarzacz mp3.
 Takie przyporządkowanie nazywamy funkcją.
Takie przyporządkowanie nazywamy funkcją.Powiemy, że:
- funkcja \(f\) przyporządkowuje Adamowi książkę,
- funkcja \(f\) przyporządkowuje Bartkowi piłkę,
- funkcja \(f\) przyporządkowuje Czarkowi odtwarzacz mp3.
- \(f(\text{Adam}) = \text{książka}\),
- \(f(\text{Bartek}) = \text{piłka}\),
- \(f(\text{Czarek}) = \text{odtwarzacz mp3}\).
| Chłopiec | Adam | Bartek | Czarek |
| Otrzymany przedmiot | książka | piłka | odtwarzacz mp3 |
- Dziedziną tej funkcji jest zbiór \(X=\{\text{Adam}, \text{Bartek}, \text{Czarek}\}\).
- Przeciwdziedziną jest zbiór \(Y=\{\text{książka}, \text{piłka}, \text{odtwarzacz mp3}\}\).
- Zbiorem wartości jest cały zbiór \(Y\).
Rozważmy funkcję \(f\) przyporządkowująca dowolnemu słowu pierwszą literę tego słowa. Oto przykład działania tej funkcji na kilku różnych słowach: \[f(\text{Adam}) = \text{A}\] \[f(\text{Bartek}) = \text{B}\] \[f(\text{Czarek}) = \text{C}\] \[f(\text{dom}) = \text{d}\] \[f(\text{zebra}) = \text{z}\] \[f(\text{zegarek}) = \text{z}\] Graficzna ilustracja funkcji: 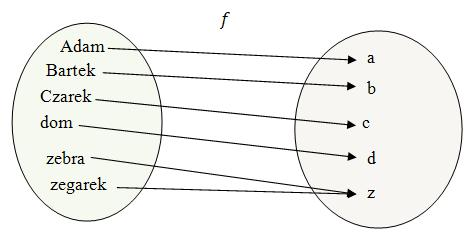 Tabela:
Tabela:
Na grafie i w tabeli pokazaliśmy tylko przykład działania tej funkcji na wybranych słowach. Sama funkcja została określona na zbiorze wszystkich możliwych słów, czyli możemy zapisać, że:
 Tabela:
Tabela: | Słowo | Adam | Bartek | Czarek | dom | zebra | zegarek |
| Pierwsza litera | A | B | C | d | z | z |
- Dziedziną tej funkcji jest zbiór wszystkich słów.
- Przeciwdziedziną jest zbiór wszystkich liter.
- Zbiorem wartości jest zbiór wszystkich liter, na które zaczyna się przynajmniej jedno słowo.
Rozważmy funkcję \(f\) przyporządkowującą każdemu słowu ze zbioru \[X=\{\text{Adam}, \text{Bartek}, \text{Czarek}, \text{dom}, \text{zebra}, \text{zegarek}\}\] liczbę liter z których składa się dane słowo.
W tym przypadku działanie funkcji będzie następujące:
\[f(\text{Adam}) = 4\] \[f(\text{Bartek}) = 6\] \[f(\text{Czarek}) = 6\] \[f(\text{dom}) = 3\] \[f(\text{zebra}) = 5\] \[f(\text{zegarek}) = 7\] Graficzna ilustracja funkcji: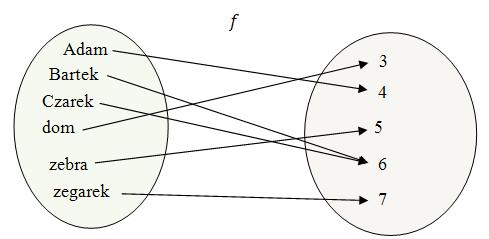 Tabela:
Tabela:
W tym przypadku działanie funkcji będzie następujące:
\[f(\text{Adam}) = 4\] \[f(\text{Bartek}) = 6\] \[f(\text{Czarek}) = 6\] \[f(\text{dom}) = 3\] \[f(\text{zebra}) = 5\] \[f(\text{zegarek}) = 7\] Graficzna ilustracja funkcji:
 Tabela:
Tabela: | Słowo | Adam | Bartek | Czarek | dom | zebra | zegarek |
| Liczba liter | 4 | 6 | 6 | 3 | 5 | 7 |
- Dziedziną tej funkcji jest zbiór \(X=\{\text{Adam}, \text{Bartek}, \text{Czarek}, \text{dom}, \text{zebra}, \text{zegarek}\}\).
- Zbiorem wartości jest zbiór \(\{3,4,5,6,7\}\).
Metody prezentowania funkcji
Funkcję można zapisać za pomocą:- opisu słownego
- grafu
- tabeli
- wzoru
- wykresu
Dla różnych funkcji różne metody prezentacji mogą być lepsze lub gorsze. Metoda grafu i tabeli często pozwala pokazać wartości funkcji jedynie dla wybranych argumentów.
Najlepsza metoda prezentowania funkcji, to wzór i wykres.
Najlepsza metoda prezentowania funkcji, to wzór i wykres.
Mając dany wzór funkcji możemy narysować jej wykres, sporządzić tabelkę, a co najważniejsze - określić wszystkie własności danej funkcji.
Istnieją dwa równoważne sposoby zapisywania wzorów funkcji. Można to zrobić w taki sposób:
\[y = \text{[tu piszemy wzór funkcji]}\] albo w taki: \[f(x) = \text{[tu piszemy wzór funkcji]}\]
Istnieją dwa równoważne sposoby zapisywania wzorów funkcji. Można to zrobić w taki sposób:
\[y = \text{[tu piszemy wzór funkcji]}\] albo w taki: \[f(x) = \text{[tu piszemy wzór funkcji]}\]
Funkcja \(f\) przyporządkowuje każdej liczbie ze zbioru: \(\{-2,-1,0,1,2\}\) liczbę ze zbioru \(\{0,1,2,3,4\}\), która jest jej kwadratem.
Obliczmy wartości tej funkcji dla wszystkich argumentów: \[ \begin{split} &f(-2)=(-2)^2=4\\[6pt] &f(-1)=(-1)^2=1\\[6pt] &f(0)=0^2=0\\[6pt] &f(1)=1^2=1\\[6pt] &f(2)=2^2=4\\[6pt] \end{split} \] Graf dla tej funkcji to: 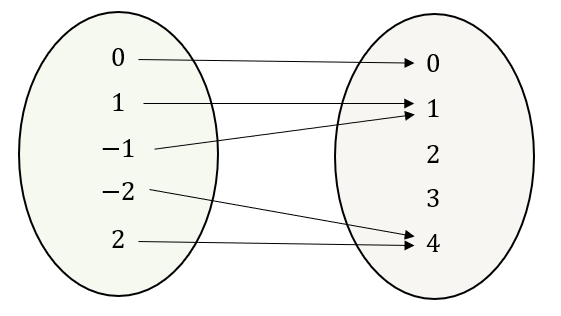 Tabela:
Tabela: | \(x\) | \(-2\) | \(-1\) | \(0\) | \(1\) | \(2\) |
| \(f(x)\) | \(4\) | \(1\) | \(0\) | \(1\) | \(4\) |
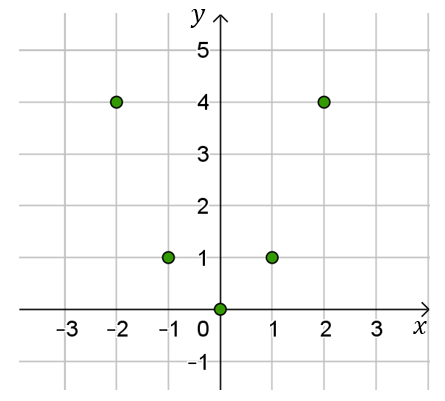
- Dziedziną tej funkcji jest zbiór \(X=\{-2,-1,0,1,2\}\).
- Przeciwdziedziną tej funkcji jest zbiór \(Y=\{0,1,2,3,4\}\).
- Zbiorem wartości jest zbiór \(\{0,1,4\}\).
Rozważmy funkcję \(f\), która przyporządkowuje każdej liczbie rzeczywistej dodatniej jej odwrotność.
Najpierw zapiszemy wzór tej funkcji: \[f(x)=\frac{1}{x}\] Teraz możemy obliczyć kilka przykładowych wartości funkcji: \[ \begin{split} &f\left(\frac{1}{3}\right)=3\\[6pt] &f\left(\frac{1}{2}\right)=2\\[6pt] &f(1)=1\\[6pt] &f(2)=\frac{1}{2}\\[6pt] &f(3)=\frac{1}{3}\\[6pt] &f(4)=\frac{1}{4}\\[6pt] \end{split} \] Możemy sporządzić tabelkę dla wybranych argumentów: | \(x\) | \(\frac{1}{3}\) | \(\frac{1}{2}\) | \(1\) | \(2\) | \(3\) |
| \(f(x)\) | \(3\) | \(2\) | \(1\) | \(\frac{1}{2}\) | \(\frac{1}{3}\) |
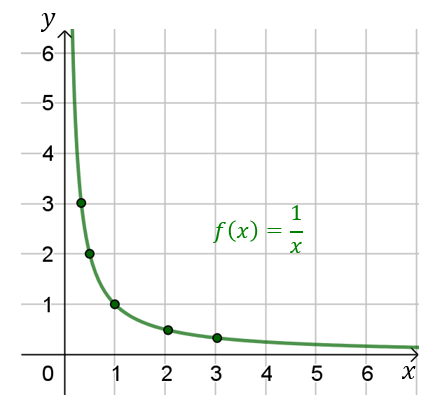 Na wykresie zaznaczyłem pięć punktów, które wcześniej wyliczyliśmy i wypisaliśmy w tabeli. Dzięki takim wcześniejszym wyliczeniom łatwiej jest narysować wykres funkcji, ponieważ wiadomo, przez jakie punkty musi przechodzić.
Na wykresie zaznaczyłem pięć punktów, które wcześniej wyliczyliśmy i wypisaliśmy w tabeli. Dzięki takim wcześniejszym wyliczeniom łatwiej jest narysować wykres funkcji, ponieważ wiadomo, przez jakie punkty musi przechodzić. - Dziedziną tej funkcji jest zbiór wszystkich liczb rzeczywistych dodatnich, czyli \(X=\mathbb{R}_+\).
- Zbiorem wartości jest zbiór wszystkich liczb rzeczywistych dodatnich, czyli \(\mathbb{R}_+\).
Definicje (mało istotne)
Czasami możemy spotkać takie pojęcie:- Zmienne niezależne - to inna nazwa dla dziedziny funkcji (argumentów \(x\)).
- Zmienne zależne - to inna nazwa dla zbioru wartości funkcji (\(y)\).
Jak sama nazwa wskazuje - zmienne zależne (\(y\)) zależą od zmiennych niezależnych (\(x\)).
W tym nagraniu wideo omawiam pojęcie funkcji na prostych przykładach.
W tym nagraniu wideo pokazuję co to są zmienne zależne i niezależne.
Funkcja \( f \) określona dla wszystkich liczb całkowitych dodatnich, przyporządkowuje liczbie \( x \) ostatnią cyfrę jej kwadratu. Zbiór wartości funkcji \( f \) zawiera dokładnie
A.\( 5 \) elementów
B.\( 6 \) elementów
C.\( 9 \) elementów
D.\( 10 \) elementów
Funkcja \(f\) przyporządkowuje każdej liczbie naturalnej większej od \(1\) jej największy dzielnik będący liczbą pierwszą. Spośród liczb: \(f(42\)), \(f(44)\), \(f(45)\), \(f(48)\) największa to
A.\( f(42) \)
B.\( f(44) \)
C.\( f(45) \)
D.\( f(48) \)
Tematy nadrzędne i sąsiednie