Wykres funkcji liniowej

Drukuj

Poziom podstawowy

Wykresem funkcji liniowej jest linia prosta.
Żeby narysować wykres funkcji liniowej, wystarczy wyznaczyć dwa punkty, które do niego należą.

Narysuj wykres funkcji liniowej \(y=x+3\).

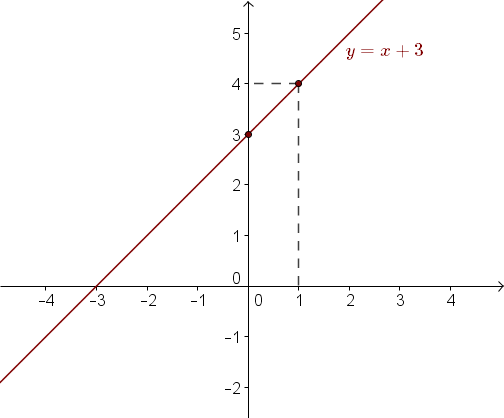
Obliczamy współrzędne dwóch dowolnych punktów przez które przechodzi nasza prosta.

Dla \(x=0\) mamy: \[y=0+3=3\] Czyli do wykresu funkcji należy punkt o współrzędnych \((0,3)\).

Dla \(x=1\) mamy: \[y=1+3=4\] Czyli do wykresu funkcji należy punkt o współrzędnych \((1,4)\).

Teraz możemy zaznaczyć punkty w układzie współrzędnych i narysować prostą:

Narysuj wykres funkcji liniowej \(y=2x-1\).

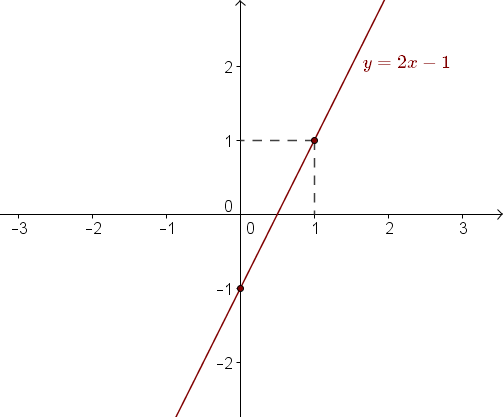
Obliczamy współrzędne dwóch dowolnych punktów przez które przechodzi nasza prosta.

Dla \(x=0\) mamy: \[y=2\cdot 0-1=0-1=-1\] Czyli do wykresu funkcji należy punkt o współrzędnych \((0,-1)\).

Dla \(x=1\) mamy: \[y=2\cdot 1-1=2-1=1\] Czyli do wykresu funkcji należy punkt o współrzędnych \((1,1)\).

Teraz możemy zaznaczyć punkty na wykresie i narysować prostą:

Narysuj wykres funkcji liniowej \(y=-\frac{1}{3}x-2\).

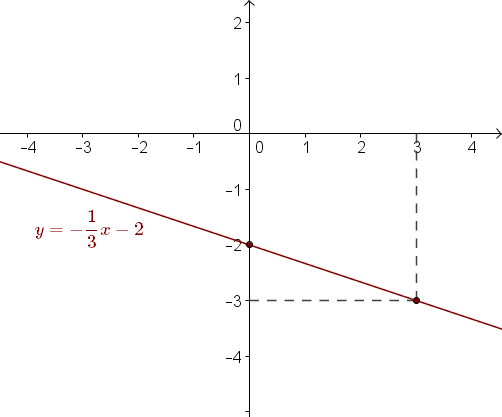
Obliczamy współrzędne dwóch dowolnych punktów przez które przechodzi nasza prosta.

Dla \(x=0\) mamy: \[y=-\frac{1}{3}\cdot 0-2=0-2=-2\] Czyli do wykresu funkcji należy punkt o współrzędnych \((0,-2)\).

Dla \(x=3\) mamy: \[y=-\frac{1}{3}\cdot 3-2=-1-2=-3\] Czyli do wykresu funkcji należy punkt o współrzędnych \((3,-3)\).

Teraz możemy zaznaczyć punkty w układzie współrzędnych i narysować prostą:

Na filmie pokazuję praktyczną metodę na szybkie rysowanie dokładnych wykresów funkcji liniowych.

Czas nagrania: 13 min.

Monotoniczność funkcji liniowej

Funkcja liniowa: \[y=ax+b\]

jest rosnąca jeżeli \(a \gt 0\),
jest malejąca jeżeli \(a \lt 0\),
jest stała jeżeli \(a = 0\).

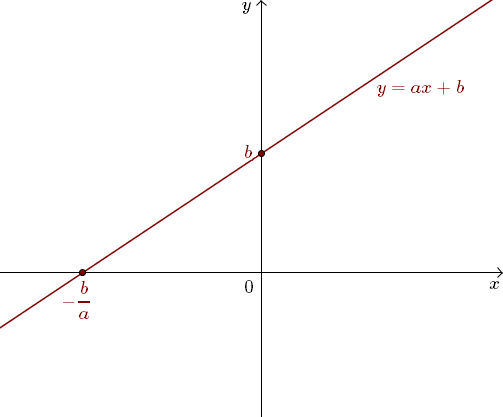Wyraz wolny \(b\), to punkt przecięcia funkcji liniowej z osią \(Oy\).

Na powyższym rysunku prosta jest rosnąca, czyli \(a \gt 0\).

Dla jakiego parametru \(m\) funkcja \(f(x)=(2m+3)x-7\) jest rosnąca?

Funkcja \(f\) jest rosnąca, jeżeli: \[\begin{split} 2m+3&\gt0\\[6pt] 2m&\gt-3\\[6pt] m&\gt-\frac{3}{2} \end{split}\] Zatem funkcja \(f\) jest rosnąca dla \(m \gt-\frac{3}{2}\).

Miejsce zerowe

Miejsce zerowe funkcji liniowej \(f(x)=ax+b\), to argument \(x\) spełniający równanie: \[ax+b=0\] Z powyższego równania wynika bezpośredni wzór: \[x=-\frac{b}{a}\]

Oblicz miejsce zerowe funkcji \(f(x)=5x-7\).

Przyrównujemy wzór funkcji do zera: \[\begin{split} 5x-7&=0\\[6pt] 5x&=7\\[6pt] x&=\frac{7}{5} \end{split}\] Zatem miejscem zerowym funkcji \(f\) jest argument \(x=\frac{7}{5}\).

Proste równoległe i prostopadłe

Dwie proste o równaniach \[\begin{split} &y=a_1x+b_1\\[6pt] &y=a_2x+b_2 \end{split}\]

są równoległe, jeżeli ich współczynniki kierunkowe są równe, czyli: \[a_1=a_2\]
są prostopadłe, jeżeli ich współczynniki kierunkowe spełniają zależność: \[a_1\cdot a_2=-1\]

Więcej materiałów o prostych równoległych i prostopadłych znajdziesz w rozdziale: Proste równoległe i prostopadłe.

Na rysunku przedstawiony jest fragment wykresu pewnej funkcji liniowej \(y=ax+b\).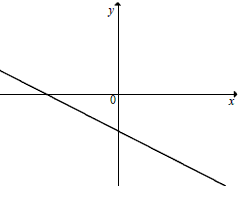

Jakie znaki mają współczynniki \(a\) i \(b\)?

A.\(a\lt 0\) i \(b\lt 0\)

B.\(a\lt 0\) i \(b>0\)

C.\(a>0\) i \(b\lt 0\)

D.\(a>0\) i \(b>0\)

Jeden z rysunków przedstawia wykres funkcji liniowej \(f(x)=ax+b\), gdzie \(a>0\) i \(b\lt 0\). Wskaż ten wykres.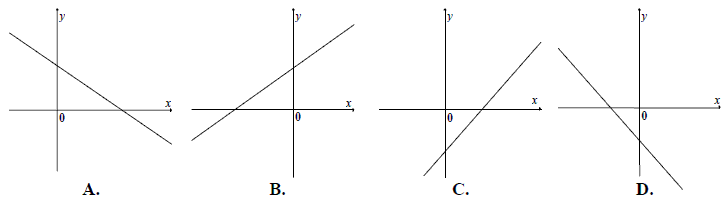

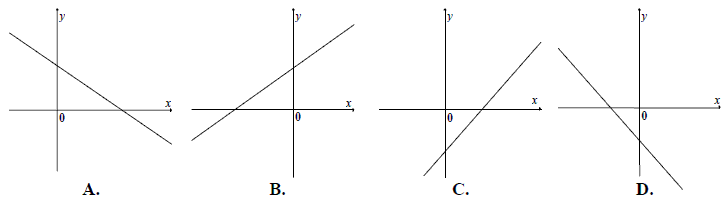
Funkcja \(f(x) = 0{,}5x - 6\)

A.jest malejąca i jej wykres przechodzi przez punkt \((0, 6)\)

B.jest rosnąca i jej wykres przechodzi przez punkt \((0, 6)\)

C.jest malejąca i jej wykres przechodzi przez punkt \((0, -6)\)

D.jest rosnąca i jej wykres przechodzi przez punkt \((0, -6)\)

Funkcja liniowa \( f(x)=(m^2-4)x+2 \) jest malejąca, gdy

A.\(m\in (-\infty,-2) \)

B.\(m\in (2,+\infty) \)

C.\(m\in \lbrace -2,2 \rbrace \)

D.\(m\in (-2,2) \)

Funkcja liniowa \( f(x)=ax+b\ \) jest rosnąca i ma dodatnie miejsce zerowe. Stąd wynika, że

A.\(a>0\) i \( b>0 \)

B.\(a\lt 0\) i \( b\lt 0 \)

C.\(a\lt 0\) i \( b>0 \)

D.\(a>0\) i \( b\lt 0 \)

Na rysunku przedstawiono fragment prostej o równaniu \(y=ax+b\).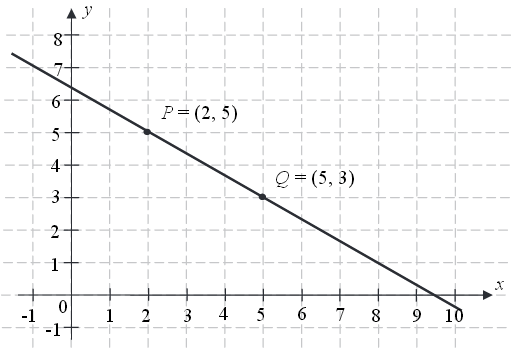

Współczynnik kierunkowy tej prostej jest równy

A.\( a=-\frac{3}{2} \)

B.\( a=-\frac{2}{3} \)

C.\( a=-\frac{2}{5} \)

D.\( a=-\frac{3}{5} \)

Wykres funkcji liniowej \(y = 2x − 3\) przecina oś \(Oy\) w punkcie o współrzędnych

A.\( (0,-3) \)

B.\( (-3,0) \)

C.\( (0,2) \)

D.\( (0,3) \)

Funkcja \(f\) jest określona dla każdej liczby rzeczywistej \(x\) wzorem \(f(x)=(m\sqrt{5}-1)x+3\). Ta funkcja jest rosnąca dla każdej liczby \(m\) spełniającej warunek

A.\( m\gt\frac{1}{\sqrt{5}} \)

B.\( m\gt1-\sqrt{5} \)

C.\( m\lt\sqrt{5}-1 \)

D.\( m\lt\frac{1}{\sqrt{5}} \)

Wykres funkcji liniowej \(f(x)=\frac{8-3x}{2}\) przecina osie układu współrzędnych w punktach \(A\) i \(B\). Pole trójkąta \(ABO\), w którym punkt \(O\) jest początkiem układu współrzędnych, wynosi:

A.\( 10\frac{2}{3} \)

B.\( 5\frac{1}{3} \)

C.\( 21\frac{1}{3} \)

D.\( 7\frac{1}{2} \)

Na wykresie funkcji liniowej określonej wzorem \(f(x)=(m-1)x+3\) leży punkt \(S=(5,-2)\). Zatem

A.\( m=1 \)

B.\( m=2 \)

C.\( m=-1 \)

D.\( m=0 \)

Na rysunku przedstawiono fragment wykresu funkcji liniowej \(f\) określonej wzorem \(f(x)=ax+b\).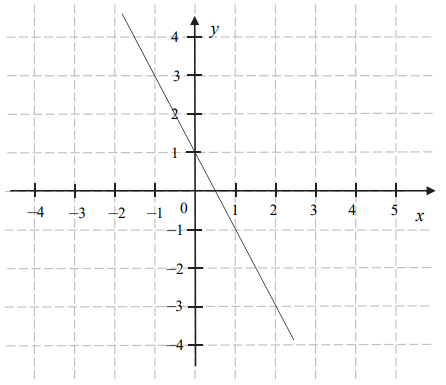

Współczynniki \(a\) oraz \(b\) we wzorze funkcji \(f\) spełniają zależność

A.\( a+b\gt0 \)

B.\( a+b=0 \)

C.\( a\cdot b\gt0 \)

D.\( a\cdot b\lt0 \)

Dana jest funkcja liniowa \(f\) określona wzorem\(f(x)=ax+b\), gdzie \(a\) i \(b\) są liczbami rzeczywistymi. Wykres funkcji \(f\) przedstawiono w kartezjańskim układzie współrzędnych \((x,y)\) na rysunku poniżej.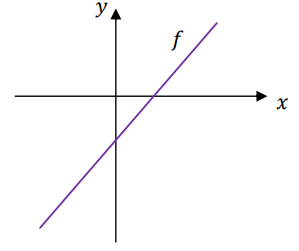

Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.

Współczynniki \(a\) i \(b\) we wzorze funkcji \(f\) spełniają warunki

A.\( a\gt 0 \) i \(b\gt 0\).

B.\( a\gt 0 \) i \(b\lt 0\).

C.\( a\lt 0 \) i \(b\gt 0\).

D.\( a\lt 0 \) i \(b\lt 0\).

Funkcja liniowa \(f\) jest określona wzorem \(f(x) = ax + b\), gdzie \(a\) i \(b\) są pewnymi liczbami rzeczywistymi. Na rysunku obok przedstawiono fragment wykresu funkcji \(f\) w kartezjańskim układzie współrzędnych \((x, y)\).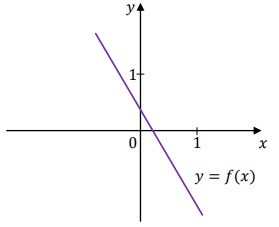

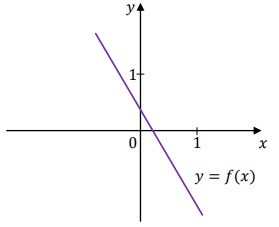
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.

Liczba \(a\) oraz liczba \(b\) we wzorze funkcji \(f\) spełniają warunki:

A.\( a\gt 0\ \) i \(\ b\gt 0\)

B.\( a\gt 0\ \) i \(\ b\lt 0 \)

C.\( a\lt 0\ \) i \(\ b\gt 0 \)

D.\( a\lt 0\ \) i \(\ b\lt 0 \)

Funkcja liniowa \(f(x)=6-2x\) przyjmuje wartości nieujemne wtedy i tylko wtedy, gdy:

A.\( x\in (-\infty, 3\rangle \)

B.\( x\in \langle 3, +\infty ) \)

C.\( x\in (-\infty, 3) \)

D.\( x\in (3, +\infty ) \)

Funkcja liniowa \(f\) przyjmuje wartość \(2\) dla argumentu \(0\), a ponadto \(f(4)-f(2)=6\). Wyznacz wzór funkcji \(f\).

Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.

W kartezjańskim układzie współrzędnych \((x, y)\) wykresy funkcji liniowych \(f(x) = (2m + 3)x + 5\) oraz \(g(x) = -x\) nie mają punktów wspólnych dla

A.\( m=-2 \)

B.\( m=-1 \)

C.\( m=1 \)

D.\( m=2 \)