Wektory

Drukuj

Poziom podstawowy

Wektor - to uporządkowana para punktów (strzałka wyznaczona przez dwa punkty)

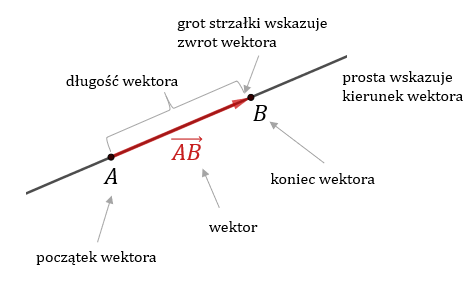
Wektor ma trzy cechy, które go jednoznacznie wyznaczają:

długość (czasami inaczej zwana modułem lub wartością)
kierunek (kierunek prostej zawierającej wektor)
zwrot (grot strzałki)

Jeżeli znamy punkt w którym wektor ma początek, to taki wektor nazywamy wektorem zaczepionym.
Wektor zaczepiony w punkcie \(A\) i o końcu w punkcie \(B\) zapiszemy tak: \(\overrightarrow{AB} \).

Jeżeli wektor może być opisany tylko przez długość, kierunek i zwrot. Wtedy taki wektor nazywamy wektorem swobodnym i oznaczamy najczęściej małymi literami, np. tak: \(\overrightarrow{v} \), \(\overrightarrow{u}\), \(\overrightarrow{w}\).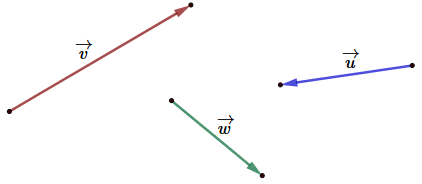

Wektory swobodne

Pojęcia: wektor zaczepiony oraz wektorem swobodnym są w praktyce rzadko stosowane. Najczęściej oba rodzaje wektorów określa się krótko pojęciem: wektor.

W równoległoboku \(ABCD\) wektory zaczepione \(\vec{AD}\) i \(\vec{BC}\) wyznac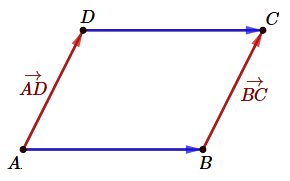zają ten sam wektor swobodny:

Podobnie wektory \(\vec{AB}\) i \(\vec{DC}\) wyznaczają ten sam wektor swobodny.
Zauważmy, że kolejność punktów ma znaczenie. Wektor \(\vec{CD}\) ma przeciwny zwrot do wektora \(\vec{DC}\).
Zatem wektory \(\vec{AB}\) i \(\vec{CD}\) nie wyznaczają tego samego wektora swobodnego.

Jeżeli dane są punkty \(A=(x_1,y_1)\) oraz \(B=(x_2,y_2)\), to współrzędne wektora \(\vec{AB}\) określa wzór: \[\vec{AB}=[x_2-x_1,y_2-y_1]\]

Współrzędne wektora zapisujemy w nawiasach kwadratowych, np.: \[\vec{v}=[3, 4]\qquad \vec{AB}=[2,-1]\] Pierwsza współrzędna oznacza przesunięcie wzdłuż osi \(Ox\), a druga wzdłuż osi \(Oy\).

Narysujmy wektory: \(\vec{v}=[3, 4]\) oraz \(\vec{AB}=[2, -1]\):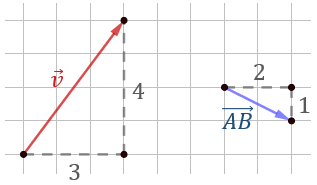

Współrzędna \(y\)-owa wektora \(\vec{AB}\) jest ujemna i dlatego przesuwamy się w dół. Na rysunku pionowe przesunięcie zostało podpisane dodatnią liczbą \(1\), ponieważ długość odcinka jest zawsze dodatnia.

Długość wektora o danych współrzędnych \(\vec{AB}=[x,y]\) obliczamy ze wzoru: \[|\vec{AB}|=\sqrt{x^2+y^2}\]

Oblicz współrzędne wektora o początku w punkcie \(A=(5,2)\) i końcu w punkcie \(B=(-3, 8)\). Oblicz długość wektora \(\vec{AB}\).

Najpierw liczymy współrzędne wektora: \[\vec{AB}=[-3-5,8-2]=[-8,6]\]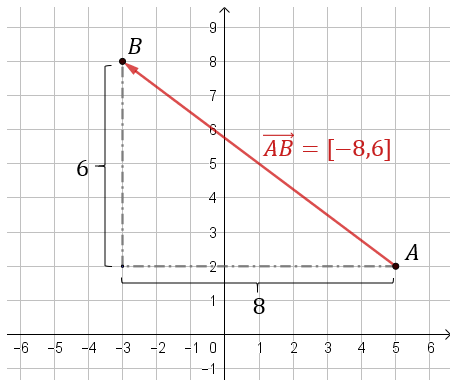

Teraz możemy obliczyć jego długość: \[|\vec{AB}|=\sqrt{(-8)^2+6^2}=\sqrt{64+36}=\sqrt{100}=10\]

Wektor przeciwny - to taki, który ma współrzędne przeciwnych znaków.
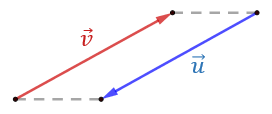
Jeżeli wektory \(\vec{v}\) i \(\vec{u}\) są przeciwne, to mają tą samą długość i kierunek, ale przeciwne zwroty.

Znajdź wektor przeciwny \(\vec{u}\) do wektora:

\(\vec{v}=[5,11]\)

\(\vec{v}=[-4,0]\)

\(\vec{v}=\left[-\frac{1}{2},3\right]\)

\(\vec{u}=-\vec{v}=[-5,-11]\)

\(\vec{u}=-\vec{v}=[4,0]\)

\(\vec{u}=-\vec{v}=\left[\frac{1}{2},-3\right]\)

Dodawanie wektorów wykonujemy dodając ich współrzędne.

Wykonaj dodawanie wektorów \(\vec{v}=[2,3]\) i \(\vec{w}=[4,-1]\)

\[\vec{v}+\vec{w}=[2,3]+[4,-1]=[2+4,3+(-1)]=[6,2]\]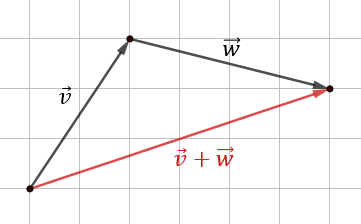

Dodawanie wektorów - interpretacja graficzna

Odejmowanie wektorów wykonujemy odejmując ich współrzędne.

Wykonaj odejmowanie wektorów \(\vec{v}=[2,3]\) i \(\vec{w}=[4,-1]\)

\[\vec{v}-\vec{w}=[2,3]-[4,-1]=[2-4,3-(-1)]=[-2,4]\]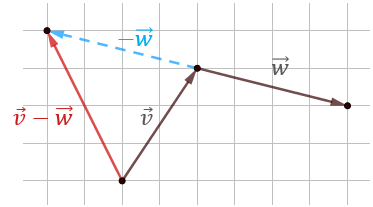

Odejmowanie wektorów - interpretacja graficzna